Allgemeines
Das Zusatzmodul RF-/BETON Stützen bemisst Druckglieder aus Stahlbeton mit dem im Eurocode 2, Kapital 5.8.8 beschriebenen Nennkrümmungsverfahren. Dieses Verfahren ist aus anderen Normen auch unter dem Namen Modellstützenverfahren bekannt. In einem früheren Artikel wurde bereits detailliert auf die Ermittlung der anzusetzenden Lastexzentrizitäten im Zuge des Nennkrümmungsverfahrens eingegangen. Aus diesem Grund wird die Ermittlung der einzelnen Exzentrizitäten hier nicht mehr detailliert beschrieben.
Getrennte Bemessung in Hauptachsenrichtung ohne Berücksichtigung der zweiachsigen Momenteninteraktion
Gemäß 5.8.9 (2), EN 1992-1-1 [1] darf eine Stütze mit zweiachsiger Lastausmitte durch getrennte Bemessung in beide Hauptachsenrichtungen ohne Beachtung der Momenteninteraktion erfolgen, wenn die Grenzen der Gleichungen 5.38a und 5.38b [1] eingehalten sind. Die Beschreibung der Gleichungen finden man im oben genannten Artikel. Hintergrund dieser Schranken beziehungsweise dieses Bemessungsansatzes ist, dass eine der beiden Lastausmitten den dominanten, die zweite den untergeordnete Wert darstellt.
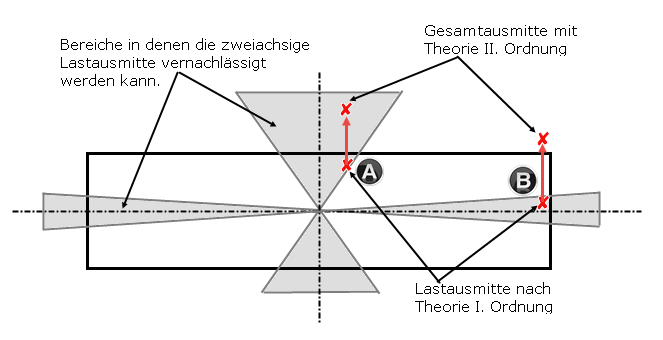
Bei der Bemessung in die getrennten Hauptachsenrichtungen ist dabei die zusätzliche Ausmitte aus Imperfektion nur in die dominante, sprich in die maßgebende Richtung zu berücksichtigen. Bild 01 zeigt, in welchen Bereichen die zweiachsige Biegung vernachlässigbar ist. Befindet sich die ausmittige Normalkraft in den schattierten Bereichen, so kann die Stütze in die beiden Hauptrichtungen getrennt bemessen werden. Es wird darauf hingewiesen, dass hierbei die Lastexzentrizitäten nach Theorie II. Ordnung in die jeweiligen Hauptachsenrichtungen zu berücksichtigen sind.
Den Hintergrund hierfür verdeutlicht ebenfalls Bild 01. Die Punkte A und B in Bild 01 sollen zwei Beispiele für eine mögliche Lastposition symbolisieren, bei der sich der Einfluss der Ausmitte nach Theorie II. Ordnung unterschiedlich auswirkt. Ohne Berücksichtigung der Theorie II. Ordnung (e2) befinden sich beide Punkte in den schraffierten und zulässigen Bereichen, in denen die zweiachsige Biegebemessung vernachlässigt werden kann. Bei Berücksichtigung der Exzentrizität nach Theorie II. Ordnung reduziert sich für den Punkt A die zweiachsige Lastausmitte, wohingegen bei der Lastposition B die zweiachsige Biegung erhöht und die Last aus dem zulässigen Bereich verschoben wird.
Getrennte Bemessung in Hauptachsenrichtung mit Berücksichtigung der zweiachsigen Momenteninteraktion
Werden die Bedingungen der Gleichung 5.38a und Gleichung 5.38b [1] nicht erfüllt, so sind die Voraussetzungen für die getrennte Bemessung in die Hauptachsenrichtung ohne der Berücksichtigung der zweiachsigen Momenteninteraktion nach 5.8.9 (2) nicht gegeben. Der Absatz (4) des Kapitels 5.8.9 [1] beschreibt mit der Gleichung 5.39 einen vereinfachten Ansatz, mit dem die zweiachsige Momenteninteraktion mit vorangegangener Bemessung der einzelnen Hauptachsenrichtungen berücksichtigt werden kann.
Mit der nachfolgenden Gleichung 5.39 [1] wird die Momenteninteraktion vereinfacht berücksichtigt.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
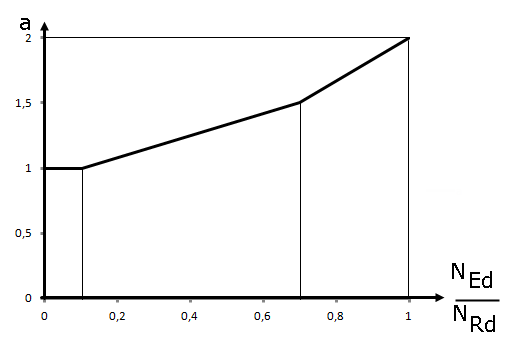
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
Bild 02 zeigt den Exponenten a in Abhängigkeit des Verhältnisses NEd/NRd. NRd ist dabei der Bemessungswert der zentrischen Normaltragfähigkeit und kann mit NRd = Ac ⋅ fcd + As + fyd bestimmt werden. Ac stellt hier die Bruttoquerschnittsfläche, As die Längsbewehrungsfläche und fcd beziehungsweise fyd die Bemessungsfestigkeiten der verwendeten Materialien dar.
Bei der Verwendung der Gleichung 5.39 [1] ist weiter zu beachten, dass die beiden Biegewiderstände MRdy und MRdz unter einer konstant bleibenden Normalkraft aus dem Bemessungsinteraktionsdiagrammen für die beiden Hauptrichtungen zu entnehmen sind (siehe Bild 03).
In Bild 03 ist ein Quadrant eines 3-dimensionalen My-Mz-N-Interaktiondiagrammes abgebildet. Gleichung 5.39 basiert darauf, vereinfacht einen horizontalen Schnitt bei NEd durch des 3D-Interaktionsdiagramm zu legen und mittels des Exponenten a ein vereinfachtes My-Mz-Momentenintaraktionsdiagramm zu generieren. In Bild 03 wurde das tatsächliche My-Mz-Momenteninteraktionsdiagramm für die Normalkraft NEd (horizontaler Schnitt) rot schattiert dargestellt. Das nach Gleichung 5.39 vereinfacht angesetzte Interaktionsdiagramm wurde zum Vergleich in Bild 04 ebenfalls rot schattiert. Bild 04 zeigt in Abhängigkeit des Exponenten a den in Gleichung 5.39 [1] angesetzten Verlauf der Momenteninteraktion.
Der Vorteil dieser vereinfachten Vorgehensweise nach Gleichung 5.39 [1] liegt darin, dass mittels der bekannten M-N-Interaktionsdiagramme für einachsige Biegung mit Normalkraft auch Druckglieder mit zweiachsiger Ausmitte schnell und einfach bemessen werden können.
Genaue Bemessung des Querschnittes mit zweiachsiger Lastausmitte
Eine genaue Bemessung eines Querschnittes mit Normalkraft und zweiachsiger Biegung benötigt eine iterative Berechnung der Qerschnittsdehnungen. Die Berechnung dieser Querschnittdehnungen ist nur noch mit einem Rechenprogramm möglich. Der Nachweis der Tragfähigkeit ist erbracht, wenn sich die Belastung innerhalb des Mres–N–Interaktionsdiagrammes (grau schattierter Bereich in Bild 03) oder in dem genau ermittelten Mz-My-Momentendiagramm (rot schattierter Bereich in Bild 03) befindet. Durch die genaue Ermittlung der Grenzkurven können für die Bemessung weitere Tragreserven generiert werden.
Zusammenfassung
Bei einer zweiachsigen Lastausmitte ermöglicht die Norm je nach Laststellung unterschiedliche Bemessungsvarianten. Bei Einhaltung der Randbedingungen der Gleichungen 5.38a und 5.38b [1] kann die zweiachsige Momenteninteraktion vernachlässigt und die Bemessung in die Hauptachsenrichtungen durchgeführt werden. Im Falle einer Überschreitung der vorgenannten Grenzen muss die Momenteninteraktion bei der Bemessung berücksichtigt werden. Dies ist vereinfacht mit der Interaktionsformel gemäß Gleichung 5.39 [1] oder mittels einer genauen zweiachsialen Querschnittsanalyse möglich. Alle erläuterten Bemessungsansätze sind in RF-/BETON Stützen enthalten.