General
El módulo adicional RF-/CONCRETE Columns calcula elementos de compresión de hormigón armado por medio del método basado en la curvatura nominal como se describe en el Eurocódigo 2, capítulo 5.8.8. Otras normas describen este método como el método del pilar modelo. En un artículo anterior se describe en detalle la determinación de las excentricidades de carga que se deben aplicar cuando se usa el método basado en la curvatura nominal. Por esta razón, aquí no se describirá en detalle la determinación de las excentricidades individuales.
Cálculo por separado en la dirección del eje principal sin considerar la interacción del momento biaxial
Según 5.8.9 (2), EN 1992-1-1 [1], se permite calcular un pilar con una excentricidad de carga biaxial por separado en ambas direcciones del eje principal sin tener en cuenta la interacción del momento, si se cumplen los límites de las ecuaciones 5.38a y 5.38b [1]. Las ecuaciones se describen en el artículo anteriormente enlazado. Estos límites y el enfoque de cálculo se basan en el hecho de que una de las dos excentricidades de carga representa el valor dominante y la segunda representa el valor subordinado.
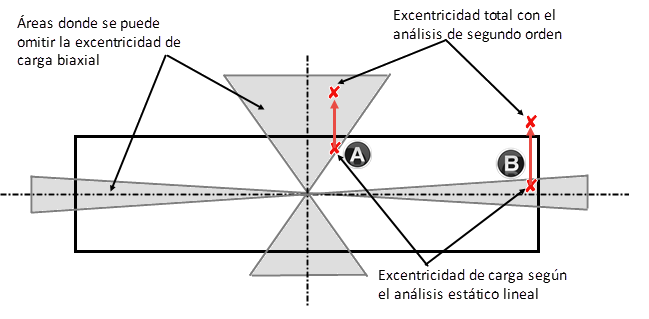
Al calcular en las direcciones separadas del eje principal, la excentricidad adicional de la imperfección se debe considerar sólo en la dirección dominante, lo que quiere decir en la dirección determinante. La figura 01 muestra qué áreas no se deben considerar para la flexión biaxial. Si la fuerza excéntrica axil está en las áreas sombreadas, puede calcular el pilar por separado en ambas direcciones principales. Tenga en cuenta que las excentricidades de carga se deben considerar según el análisis de segundo orden en las respectivas direcciones del eje principal.
Esto también se muestra en la figura 01. Los puntos A y B de la figura 01 representan dos ejemplos de una posible posición de carga donde la influencia de la excentricidad según el análisis de segundo orden tiene efectos diferentes. Sin considerar el análisis de segundo orden (e2), ambos puntos se sitúan en áreas sombreadas y admisibles donde se puede omitir el cálculo de la flexión biaxial. Cuando se considera la excentricidad según el análisis de segundo orden, la excentricidad de carga biaxial se reduce para el punto A, mientras que para la ubicación de la carga B, la flexión biaxial aumenta y la carga se desplaza fuera del intervalo permitido.
Cálculo por separado en la dirección del eje principal considerando la interacción del momento biaxial
Si no se cumplen las condiciones de la ecuación 5.38a y la ecuación 5.38b [1], se cumplen los requisitos previos para el cálculo por separado en la dirección del eje principal sin considerar la interacción del momento biaxial según 5.8.9 (2). El apartado (4) del capítulo 5.8.9 [1] usa la ecuación 5.39 para describir un enfoque simplificado que puede usar para considerar la interacción del momento biaxial con el cálculo previo de las direcciones individuales del eje principal.
La siguiente ecuación 5.39 [1] tiene en cuenta la interacción del momento de forma simplificada.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
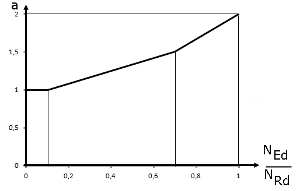
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
La figura 02 muestra el exponente a como una función de la relación NEd/NRd. NRd es el valor de cálculo de la resistencia axial céntrica y se puede determinar con NRd = Ac ⋅ fcd + As + fyd . Ac representa el área de la sección bruta, As representa el área de la armadura longitudinal, y fcd y f yd representan las resistencias de cálculo de los materiales utilizados.
Al usar la ecuación 5.39 [1], tenga en cuenta además que las dos resistencias a flexión MRdy y MRdz se deben tomar de los diagramas de interacción de cálculo para las dos direcciones principales cuando se tiene un esfuerzo axil constante (ver figura 03).
La figura 03 muestra un cuadrante de un diagrama de interacción tridimensional de My-Mz-N. La ecuación 5.39 se basa en la simplificación de una sección horizontal en NEd utilizando el diagrama de interacción 3D y al generar un diagrama simplificado de la interacción del momento My-Mz con el exponente a. En la figura 03, el diagrama de interacción del momento real My-Mz para el esfuerzo axil NEd (sección horizontal) se muestra sombreado en rojo. El diagrama de interacción simplificado según la ecuación 5.39 también está sombreado en rojo para la comparación. La figura 04 muestra, dependiendo del exponente a, la distribución de la interacción de momentos aplicada en la ecuación 5.39 [1].
La ventaja de este enfoque simplificado según la ecuación 5.39 [1] es que los elementos de compresión con excentricidades biaxiales también se pueden calcular rápida y fácilmente por medio de los diagramas de interacción M-N conocidos para flexión uniaxial con esfuerzo axil.
Cálculo exacto de la sección con excentricidad de carga biaxial
Un cálculo preciso de la sección con esfuerzo axil y flexión biaxial necesita un cálculo iterativo de las deformaciones de la sección. El cálculo de estas deformaciones de la sección sólo es posible con una herramienta de cálculo. El cálculo del estado límite último se cumple si la carga se encuentra en el diagrama de interacción Mres-N (área sombreada en gris en la figura 03) o en el diagrama de momento Mz-M y (área sombreada en rojo en la figura 03) determinado exactamente. Al determinar con precisión las curvas límite, puede generar capacidades de carga adicionales para el cálculo.
Conclusión
Para una excentricidad de carga biaxial, la norma permite diferentes variantes de cálculo en función de la posición de carga. Al respetar las condiciones de contorno de las ecuaciones 5.38a y 5.38b [1], se puede omitir la interacción del momento biaxial y se puede realizar el cálculo en las direcciones del eje principal. Si se superan los límites mencionados anteriormente, se debe considerar la interacción del momento en el cálculo. Esto es posible de forma simplificada con la fórmula de interacción según la ecuación 5.39 [1] o mediante un análisis preciso de la sección biaxial. Todos los enfoques de cálculo descritos son posibles con el módulo adicional RF-/CONCRETE Columns.