Généralités
Le module additionnel RF-/CONCRETE Columns permet de calculer des éléments béton armé en compression à l’aide de la méthode de la courbure nominale selon l’Eurocode 2, 5.8.8. Cette méthode est également appelée « méthode du poteau type » dans d’autres normes. Un précédent article de notre base de connaissance explique comment déterminer les excentrements de charge qui doivent être appliqués en cas d’utilisation de la méthode basée sur la courbure nominale. Le présent article ne détaille donc pas la détermination des excentrements individuels.
Calcul séparé dans chaque direction principale, sans tenir compte de l’interaction de moment biaxiale
Selon l'’EN 1992-1-1, 5.8.9(2) [1], il est permis de calculer un poteau avec un excentrement de charge biaxial séparément dans les deux directions d’axe principal sans considérer l’interaction des moments, si les limites des équations 5,38a et 5,38b [1] sont observées. Ces équations sont décrites dans l'article de notre base de connaissance mentionné ci-dessus. Ces conditions et cette méthode de calcul s’appuient sur le fait que l’un des deux excentrements de charge constitue la valeur déterminante tandis que l’autre représente la valeur subordonnée.
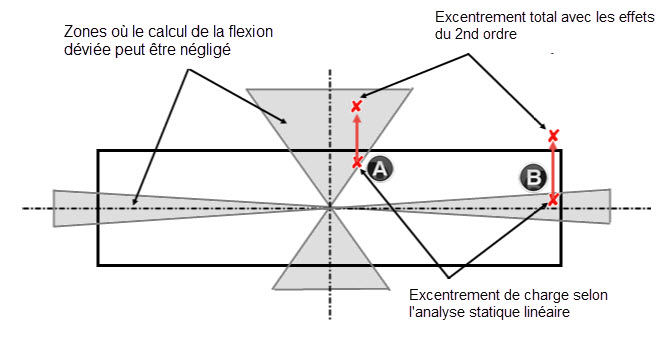
Lorsque le calcul est effectuée dans chaque direction principale, l’excentrement supplémentaire résultant des imperfections doit être considéré uniquement dans la direction déterminante. La Figure 01 indique les zones qui ne doivent pas être considérées pour la flexion déviée. Si la charge excentrée se situe dans les zones grisées, vous pouvez calculer le poteau de manière séparée dans chacune des deux directions principales. Notez que les excentrements de charge doivent être considérés selon une analyse du second ordre dans les directions principales respectives,
comme indiqué sur la Figure 01. Les points A et B de la Figure 01 représentent deux exemples de position de charge possible où les effets du second ordre ont une influence différentes sur les excentrements. Si les effets du second ordre (e2) ne sont pas considérés, ces deux points se situent dans les zones grisées et autorisées où le calcul de la flexion déviée peut être négligé. Si on considère l'excentrement avec les effets du second ordre, l’excentrement de charge biaxial est réduit pour le point A, alors que la flexion déviée augmente et que la charge se retrouve hors de la plage admissible dans le cas de la position de charge B.
Calcul séparé dans chaque direction principale, compte tenu de l’interaction de moment biaxiale
Si les conditions de l’équation 5.38a et de l’équation 5.38b [1] ne sont pas remplies, les conditions préalables pour la vérification séparée dans la direction de l’axe principal sans considérer l’interaction biaxiale des moments selon 5.8.9 (2e). La Section (4) du Chapitre 5.8.9 [1] utilise l’Équation 5.39 pour décrire une approche simplifiée que vous pouvez utiliser pour considérer l’interaction des moments biaxiaux avec le calcul précédent des directions d’axe principales individuelles.
L’équation 5.39 [1] ci-dessous considère l’interaction des moments de manière simplifiée.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
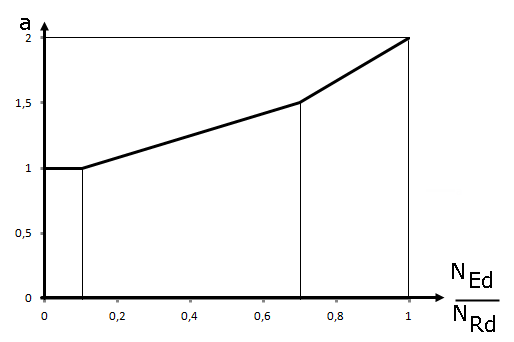
a |
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
La Figure 02 montre les valeurs de l’exposant a en fonction du rapport NEd/NRd. NRd est la valeur de calcul de la résistance axiale centrique et peut être déterminée avec NRd = Ac ⋅ fcd + As + fyd . Ac est l’aire brute de la section béton, As l’aire des armatures longitudinales et fcd ainsi que fyd sont les valeurs de calcul de la résistance des matériaux utilisés.
Lorsque vous utilisez l’Équation 5.39 [1], veuillez noter que les deux résistances en flexion MRdy et MRdz doivent être extraites des diagrammes d’interaction de calcul pour les deux directions principales en cas d’effort normal constant (voir la Figure 03).
La Figure 03 montre un quadrant d’un diagramme des interactions de My-Mz-N en 3D. L’Équation 5.39 se base sur la simplification d’une section horizontale à NEd à l’aide du diagramme des interactions en 3D et sur la génération d’un diagramme simplifié d’interaction des moments My-Mz avec l’exposant a. Le diagramme réel d’interaction des moments My-Mz pour la force axiale NEd (section horizontale) est indiqué en rouge sur la Figure 03. Le diagramme d’interaction simplifié selon l’Équation 5.39 est également en rouge, à des fins de comparaison. La Figure 04 affiche la distribution de l’interaction des moments appliquée dans l’Équation 5.39 [1], en fonction de l’exposant a.
L’avantage de cette approche simplifiée selon l’Équation 5.39 [1] est que les éléments de compression avec des excentrements biaxiaux peuvent également être calculés rapidement et facilement à l’aide des diagrammes d’interaction M-N pour la flexion uniaxiale avec des efforts internes ou l’effort normal.
Calcul précis de la section avec excentrement de charge biaxial
La vérification précise d'une section avec effort normal et flexion biaxiale nécessite un calcul itératif des déformations de cette section. Le calcul de ces déformations ne peut être réalisé qu’avec un outil dédié. La vérification à l’ELU est satisfaisante si la charge se trouve dans le diagramme d'interaction Mres-N (zone grisée sur la Figure 03) ou dans le diagramme des moments Mz-M y déterminé avec précision (zone en rouge sur la Figure 03). Déterminer précisément les courbes aux limites permet de générer des capacités de charge supplémentaires pour le calcul.
Conclusion
Différentes variantes de calcul en fonction de la position de charge sont permises par la norme dans le cas d’un excentrement de charge biaxial. En respectant les conditions aux limites des équations 5.38a et 5.38b [1], l’interaction des moments biaxiaux peut être négligée et la vérification peut être effectuée dans les directions des axes principaux. Si les limites mentionnées ci-dessus sont dépassées, l'interaction de moments doit être considérée dans le calcul. Cette opération est possible de manière simplifiée à l’aide de la formule d’interaction selon l’Équation 5.39 [1] ou à l’aide d’une analyse biaxiale exacte de la section. Le module additionnel RF-/CONCRETE Columns permet d'adopter toutes les approches de calcul décrites dans cet article.