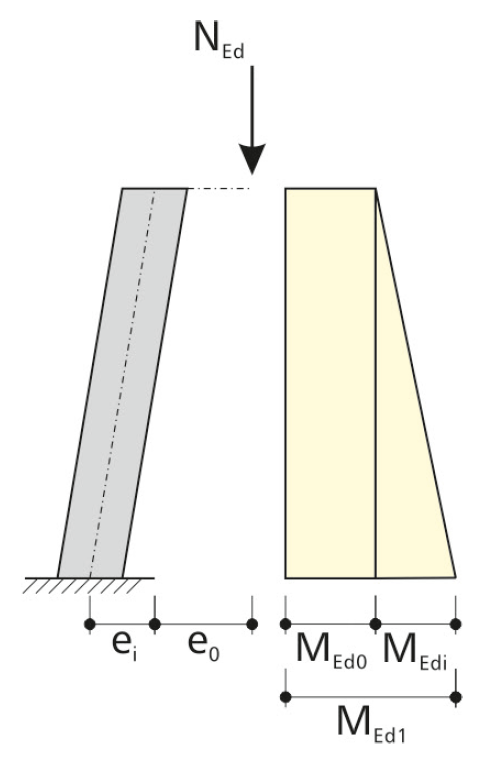
Ils résultent d'application de charge à excentrement planifié, de structures imparfaites (imperfections géométriques et matérielles) et d'une excentricité supplémentaire issue du calcul selon la théorie du second ordre.
Excentrement planifié
L'excentrement issue d'une application de charge excentrée est facile à déterminer à partir des moments issus d'une application de charge excentrée. Pour une distribution de moment constante, la relation suivante s'applique :
Dans ce cas, l'excentrement minimal selon 6.1.(4) est de
où h = hauteur de sectionPour une distribution de moment linéairement variable, un excentrement équivalent peut être déterminé, à l'aide de la formule suivante :
Les excentrements doivent alors être appliquées avec des signes. Ils ont le même signe, si les moments associés créent de la tension du même côté.
Si toute distribution de moment intervient, l'excentrement maximal est toujours utilisé, afin de n'avoir àexclure aucun poteau de la vérification.
Excentrements non souhaités dus à des imperfections
Pour le calcul des moments selon l'analyse du premier ordre, les imperfections géométriques et matérielles doivent également être considérées. Cette opération peut être effectuée en appliquant les imperfections géométriques équivalentes, considérées sous forme d'inclinaison θi.
L'excentrement est déterminé dans l'EN 1992-1-1 selon la formule (5.2) :
L'inclinaison θi est calculée selon la formule (5.1) :
Où :
Valeur de base de l'inclinaison
Facteur de réduction pour la hauteur
Facteur de réduction pour le nombre des composants structuraux (m = nombre de poteaux)
Le moment fléchissant de l'imperfection équivalente ei est ainsi :
Excentrements additionnels dus au calcul selon l'analyse du second ordre
Le poteau se courbe sous l'effet de la charge de l'effort normal et la tête de poteau est déviée selon la trajectoire e2. Il en résulte une distribution de moment selon l'analyse du second ordre.
Pour la méthode de la courbure nominale, une distribution de moment en forme de parabole est supposée. La détermination de l'excentrement selon l'analyse du second ordre est effectuée selon l'EN 1992-1-1 5.8.8.2(3).
Elle est détaillée dans les normes et le manuel de (RF-)CONCRETE Columns.
Particularités lors de la détermination des excentrements pour un excentrement de charge biaxial
Pour les poteaux soumis à des excentrements de charge biaxiaux, une vérification séparée peut être effectuée dans les deux axes principaux. Pour cette vérification, les imperfections doivent être appliquées uniquement dans la direction où elles conduisent aux effets les moins défavorables. Les vérifications doivent être effectuées dans les deux directions où toutes les armatures sont appliquées. Il s'agit donc d'exclure que les imperfections nécessitent une vérification biaxiale.
Pour que la vérification puisse s'effectuer dans les directions, et ne pas avoir à considérer plus de flexions biaxiales, les conditions doivent être remplies selon l'équation (5.38).
Pour que cette vérification séparée soit même possible, l'option correspondante dans (RF-)CONCRETE Columns doit tout d'abord être activée.
D'une part, le rapport d'élancement doit être considéré dans l'équation (5.38a) :
D'autre part, l'une des conditions quant aux excentrements de charge liés selon l'équation (5.38b) doit être remplie :
où :
iy et iz sont les rayons de giration par rapport aux axes y et z.
sont les excentrements de charge dans la direction de l'axe.
L'imperfection n'est pas prise en compte pour la direction subordonnée lors du calcul des moments de calcul MEdy et MEdz.
La direction subordonnée est déterminée via le ratio d'excentrement total à l'excentrement selon la théorie du premier ordre.
pour le calcul de (5.38b).
Sinon, ei,z est égal à 0.
Si l'une des conditions de l'équation (5.38b) est ainsi satisfaite, la vérification peut être effectuée séparément, les imperfections dans la direction subordonnée étant ainsi négligées. Si (5.38b) n'est pas satisfaite, une vérification biaxiale considérant toutes les imperfections doit être effectuée.
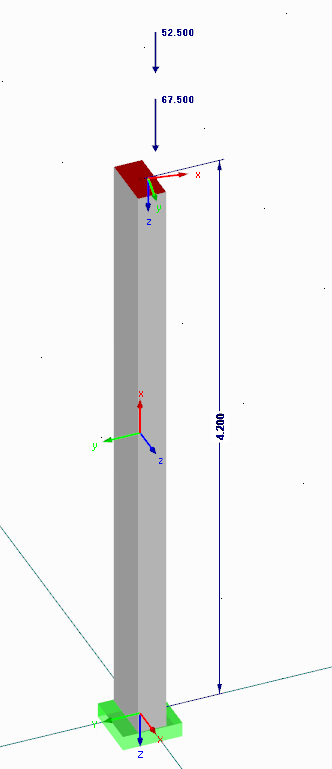
Exemple avec des tasseaux
L'excentrement sont extraites du logiciels selon l'analyse du second ordre :
e2,y = 238 mm
e2,z = 119,5 mm
Ces valeurs permettent de déterminer quelles directions sont subordonnées.
ei,z peut ainsi être paramétré sur 0 et on obtient les valeurs définies selon la Figure 06.