Ogólne informacje
Moduł dodatkowy RF-/CONCRETE Columns wymiaruje elementy ściskane z betonu zbrojonego według metody nominalnej krzywizny, opisanej w pkt. 5.8.8. Eurokodu 2. Inne normy opisują tę metodę jako metodę słupa modelowego. W jednym z poprzednich artykułów szczegółowo omówiono wyznaczanie mimośrodów w ramach metody nominalnej krzywizny. Z tego względu nie będziemy tutaj szczegółowo omawiać wyznaczania pojedynczych mimośrodów.
Oddzielne obliczenia w kierunku osi głównych bez uwzględniania interakcji momentów zginających w dwóch kierunkach
Zgodnie z 5.8.9 (2), EN 1992-1-1 [1], dozwolone jest wymiarowanie słupa z dwukierunkowym mimośrodem obciążenia osobno w obu kierunkach osi głównych bez uwzględniania interakcji momentów, jeżeli są spełnione wartości graniczne równań 5.38a i 5.38b [1]. Równania te opisano w artykule wspomnianym powyżej. Ograniczenia te i podejście obliczeniowe opierają się na fakcie, że jeden z dwóch mimośrodów obciążenia ma wartość dominującą, a drugi jest wartością podrzędną.
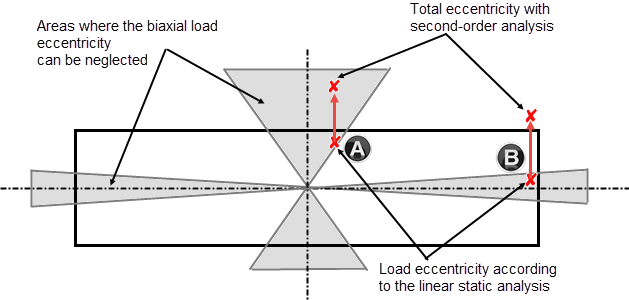
Przy obliczeniach w oddzielnych kierunkach osi głównych należy uwzględnić dodatkowy mimośród od imperfekcji tylko w dominującym, a zatem miarodajnym kierunku. Rysunek 01 pokazuje, w jakich obszarach zginanie dwukierunkowe może zostać pominięte. Jeżeli mimośrodowa siła osiowa znajduje się w obszarach zacieniowanych, słup można obliczyć oddzielnie w obu kierunkach. Należy pamiętać, że mimośrody obciążenia należy uwzględnić zgodnie z analizą drugiego rzędu w odpowiednich kierunkach osi głównych.
Wyjaśnia to również rysunek 01. Punkty A i B na rysunku 01 mają symbolizować dwa przykłady możliwego położenia obciążenia, w którym wpływ mimośrodu drugiego rzędu jest zupełnie różny. Bez uwzględnienia teorii drugiego rzędu (e2) obydwa punkty znajdują się w zakreskowanych, dopuszczalnych obszarach, w których zginanie ukośne może zostać pominięte. Przy uwzględnieniu mimośrodu według teorii drugiego rzędu wpływ dwukierunkowego mimośrodu dla punktu A ulega redukcji, natomiast w położeniu B wpływ zginania dwukierunkowego zwiększa się, a obciążenie zostaje przesunięte poza dopuszczalny zakres.
Oddzielne obliczenia w kierunku osi głównych z uwzględnieniem dwukierunkowej interakcji momentów
Jeżeli warunki z Równania 5.38a i Równania 5.38b [1] nie są spełnione, warunki wstępne dla oddzielnych obliczeń w kierunku osi głównych bez uwzględnienia interakcji momentów w obu kierunkach zgodnie z 5.8.9 (2. ). W sekcji (4) rozdz. 5.8.9 [1] posługujemy się równaniem 5.39 do opisania podejścia uproszczonego, w którym można uwzględnić interakcję momentów w dwóch osiach z wcześniejszym obliczeniem poszczególnych kierunków osi głównych.
Poniższe równanie 5.39 [1] uwzględnia interakcję momentów w sposób uproszczony.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
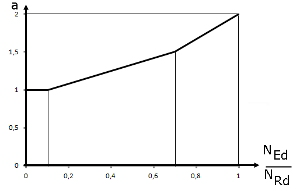
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
Rysunek 02 przedstawia wykładniki potęgi a w zależności od stosunku NEd/NRd. NRd jest wartością obliczeniową nośności przy osiowym przekroju i może byćobliczona według wzoru NRd = Ac fcd + As +fyd . Ac oznacza pole przekroju brutto, As oznacza pole przekroju zbrojenia podłużnego, a fcd iyd oznaczają wytrzymałości obliczeniowe zastosowanych materiałów.
Korzystając z równania 5.39 [1], należy pamiętać, że dwie nośności na zginanieMRdy iMRdz należy przyjąć z wykresów obliczeniowych interakcji dla dwóch głównych kierunków, jeżeli siła osiowa ( patrz Rysunek 03).
Rysunek 03 przedstawia kwadrant trójwymiarowego wykresu interakcji My-Mz-N. Równanie 5.39 opiera się na wykonaniu uproszczonego poziomego przekroju przez trójwymiarowy wykres interakcji przy określonym poziomie siły NEd i wygenerowaniu przy użyciu wykładnika a uproszczonego wykresu interakcji momentów My-Mz. Na rysunku 03 rzeczywisty wykres interakcji momentów My-Mz dla siły osiowej NEd (przekrój poziomy) jest zacieniowany na czerwono. Uproszczony wykres interakcji na rysunku 04, sporządzony na podstawie równania 5.39, dla porównania również został zacieniowany na czerwono. Rysunek 04 przedstawia, w zależności od wykładnika a, rozkład interakcji momentów zastosowany w równaniu 5.39[1].
Zaletą tego uproszczonego podejścia, zgodnego z równaniem 5.39[1], jest to, że elementy ściskane z mimośrodami dwukierunkowymi mogą być obliczane szybko i łatwo za pomocą wykresów interakcji MN dla zginania jednoosiowego ze zginaniem siła.
Dokładne obliczanie przekroju z dwukierunkowym mimośrodem
Dokładne obliczenie przekroju poddanego działaniu siły osiowej i zginania dwukierunkowego wymaga obliczeń iteracyjnych odkształceń przekroju. Jest to możliwe tylko przy użyciu odpowiedniego programu obliczeniowego. Warunek nośności przekroju jest spełniony, jeżeli obciążenie znajduje się w obrębie wykresu iteracji Mres–N (obszar zacieniowany na szaro na rysunku 03) lub na dokładnie wyznaczonym wykresie momentów Mz-My (obszar zacieniowany na czerwono na rysunku 03). Dokładne wyznaczenie krzywych granicznych umożliwia wygenerowanie dodatkowych rezerw nośności do obliczeń.
Uwagi końcowe
W przypadku zginania ukośnego norma dopuszcza różne warianty obliczeń w zależności od położenia obciążenia. Uwzględniając warunki brzegowe z równań 5.38a i 5.38b [1], można pominąć dwukierunkową interakcję momentów i przeprowadzić obliczenia w kierunkach głównych osi. W przypadku przekroczenia wspomnianych granic należy uwzględnić w obliczeniach interakcję momentów. Jest to możliwe w sposób uproszczony dzięki równaniu interakcji zgodnie z równaniem 5.39 [1] lub poprzez dokładną analizę dwuosiowego przekroju. Wszystkie opisane metody obliczeniowe są dostępne w module RF-/CONCRETE Columns.