分析的连接在附加组件钢连接使用替代钢连接有限元模型(“子模型”)进行设计。此模型是根据连接的拓扑创建的。单个设计组件如板材、焊缝或螺栓在此模型中通过基本的有限元对象——面或杆——表示,并通过像面接触或刚性耦合这样的特殊对象补充。此方法使得可以用设计标准的解析公式来比较基本组件的行为。借助该“子模型”,可以分析连接的承载能力和屈曲强度,以及刚度和变形能力。
子模型的尺寸根据连接的杆截面尺寸比例确定。用2D表面建模的杆在连接组件之外沿轴向延长为最大截面尺寸的倍数。该系数默认为1.5,但可以在承载能力配置中调整。连接最远的组件用作间距参考。
在子模型中,根据用户设置,连接杆的端部要么刚性固定,要么通过在全局模型中计算的替代荷载加载。杆端的荷载基于整体模型中的截面荷载,考虑各自的静力分析设置,并进行调整,使它们的作用力与分配给连接的节点中相关组件的截面荷载一致。杆的端部通过刚性表面加固,以防止截面歪曲并避免在加载或支撑节点上的应力集中。
默认情况下,替代钢连接有限元模型使用几何线性分析与非线性材料模型结合来计算承载能力。为分析模型的非线性,采用迭代的Newton-Raphson方法。非线性二阶分析(P-Δ)是用于屈曲评估结构分析的默认设置,而稳定性分析则使用线性特征值方法。有关更多信息,请参见RFEM手册中章节静力分析设置。
如果主模型的静力分析中考虑了二阶或三阶理论,可能会导致主模型(平衡在变形系统上建立)和子模型(力施加在未变形子模型上)之间的一致性。但是对于典型的结构系统,这种影响应可忽略不计。
材料模型
在子模型中,表示杆板和嵌入板的表面具有均匀的厚度,并且遵循各向同性塑性材料模型。应力失效假设基于von-Mises屈服准则。使用双线性图,在屈服前,材料在钢的弹性模量下弹性变形,随后塑性阶段的塑性模量为弹性模量的1/1000。
确定极限强度的标准为5%的von-Mises等效塑性应变。推荐此值,但可以在承载能力配置中调整。这使得能够利用钢的塑性行为和连接中的应力重分布。对此钢连接的实际行为进行了良好的近似。
杆和板
用于平面杆板和嵌入板的建模,使用了平面几何类型和标准刚度类型。表面具有均匀的厚度,并依照在材料模型部分中描述的各向同性塑性材料模型。表面是二维对象,位于板的中间平面中。若单个板片不能直接通过其边界线连接表示杆,则通过刚性耦合连接。线对线耦合类型连接连接板的边界线与在所连接板中创建的内线。此连接用于I型型材。
由非平面表面制成的杆或其部分,如圆形空心型材或圆角矩形空心型材,通过将弯曲段划分为较小的平面表面进行建模。这些表面具有与用于平面板的表面相同的属性。分段程度可以在承载能力配置中由用户调整。
网格
所有面的网格设置允许使用三角形和四边形有限元,以及“尽可能生成等边正方形”的选项。
每根杆的板具有相同的网格单元大小。默认情况下设置了最小和最大单元大小。根据杆的截面尺寸确定元素的大小。默认情况下,截面最长边被分为八个部分。嵌入板的网格设置单独处理:网格元素的大小根据板的最长边确定。对于没有螺栓的板,默认在长边创建八个元素,而对于有螺栓的板,默认创建16个元素。
在螺栓区域,对螺栓板的表面应用环形节点网格。在此环形节点网格中可以设置半径为螺栓孔半径的倍数,并设定孔边缘的元素数量。
对于角焊缝的替代面,可以设定沿焊缝长度的最大元素数量,以及元素的最小和最大尺寸。
网格节点通过刚性耦合和面接触与连接的线或面连接。这会影响连接面的网格,使其离散化不完全独立。
螺栓
螺栓模型由杆、面和面接触系统组成,代表螺栓的各个部件:杆柄、螺帽和螺母。每个螺栓自动在螺栓板中生成一个孔。
孔由径向排列的杆填充,称为“辐条”。作为“梁”类型的这些杆用于在螺栓杆和板之间传递剪力。杆的数量受网格设置影响,并等于孔边的元素数量。杆的横截面是一个“实心矩形”,其尺寸受螺栓板的数量和尺寸影响。它们相当于轴承中的螺栓杆面积。
在辐条与板连接的节点上分配杆端关节。关节设置为使杆不加固板中的孔,只传递板与螺栓之间的剪力。
辐条元件具有“拉断”类型的非线性,因此只有压缩的部分起作用。它们分配了各向同性线性弹性材料,与钢在弹性状态下相当。
螺栓头和螺母的模型也使用了一系列径向杆(“辐条”),因为它涉及到螺栓板的孔。然而这些辐条在其截面尺寸上有所不同,以表示螺栓头和螺母的高度。此外,这些杆的端部没有分配关节,也没有分配失效非线性。此辐条集通过一个环形面加以扩展,并与径向排列的辐条连接。对于面,使用几何类型“平面”和刚度类型“标准”,具有均匀厚度,相当于螺栓头或螺母的高度。
连接代表螺栓头、孔中的螺栓杆和螺母的径向杆系统的中心通过一根杆相连,以代表螺栓头和螺纹。分配给它的是杆类型“梁”,并称为“轴”。轴具有一个圆形横截面,其面积与螺栓的张紧截面相对应。横截面材料是各向同性线性弹性。
在连接的板之间的部分使用杆类型“刚性”。刚度矩阵相当于用于螺栓头(或螺母)和螺栓板之间的杆;唯一的区别在于大大增加的弯曲刚度。如果不调整刚度,便会在通过剪力传递力的地方导致物理上不切实际的弯曲。螺栓杆这一部分的塑性行为通过一种“图”类型的杆连接非线性在螺栓板切面的接口中实现。
在螺栓板之间以及螺栓头或螺母和这些螺栓板之间,由此产生的接触压力通过面接触传递。它们被设置在螺栓头环的表面与表示第一个螺栓板的面之间,接触的螺栓板之间,以及表示最后一个螺栓板的表面与螺母环之间。面接触类型在垂直于表面的方向上设定为“拉断”,而在与表面平行方向上的接触设定为“刚性摩擦”。此处摩擦系数设为一个接近零的值。这些接触形成在螺栓杆上引起适当张力。用作设计检查的内剪力在y和z方向上的设计张力和设计剪力在位于连接的螺栓板之间的轴上形成。
上图中的数字指示了以下组件:
| 1 | 螺栓杆 – 杆类型“刚性" |
| 2 | 螺栓孔 – 辐条 |
| 3 | 螺母 – 面环 |
| 4 | 螺母 – 辐条 |
| 5 | 螺栓杆 |
| 6 | 螺母 – 面接触 |
| 7 | 螺栓头 – 面接触 |
| 8 | 螺栓头 – 辐条 |
| 9 | 螺栓头 – 面环 |
预紧螺栓
螺栓预紧作为子模型内的独立荷载工况施加。此荷载工况螺栓预紧随即作为实际设计荷载工况的初始状态考虑。根据在承载能力配置中定义的预紧力系数(按EN 1993-1-8默认为0.7),预紧以依赖于拉伸强度的杆载荷施加于螺栓杆上。
焊缝
完全穿透的对接焊缝模型使用焊板之间的直接连接。通过刚性耦合的“线对线”类型实现。连接类似于杆截面部分(杆板)之间的连接。此刚性耦合类型使用“自定义分配”和“忽略间距影响”选项。
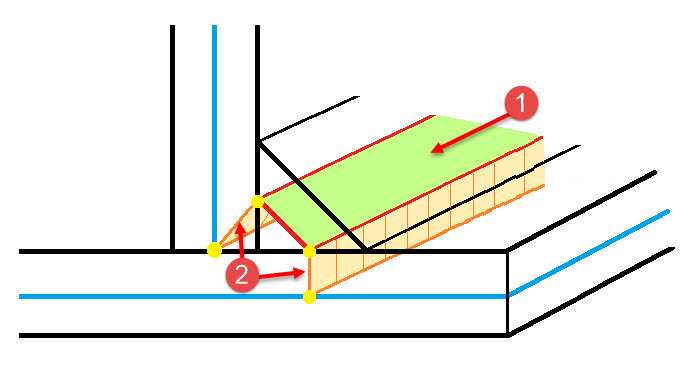
角焊缝模型也使用刚性耦合系统(见下图中的编号为➁的)和焊接连接的替代面(见下图中的编号为➀的情况)。
刚性耦合类型是“线对线”类型,带有“自定义分配”和“忽略间距影响”选项,连接焊接的板的边缘与焊接替代面的边缘,替代面的第二边与参考板。替代面位于角焊缝三角形截面的中腰部位,称为角焊缝的“焊咽厚度”。角焊缝的替代面是“标准”刚度类型,均匀厚度,具有等于该焊缝焊咽厚度的尺寸。使用一个专为失效标准拟合的正交各向同性塑性材料模型。
该焊缝材料模型被设定为与标准中考虑的焊缝行为相符。即,在替代面上仅出现与焊接应力分量σ⊥、τ⊥和τ||对应的应力方向。其他方向的替代面的刚度接近于零。
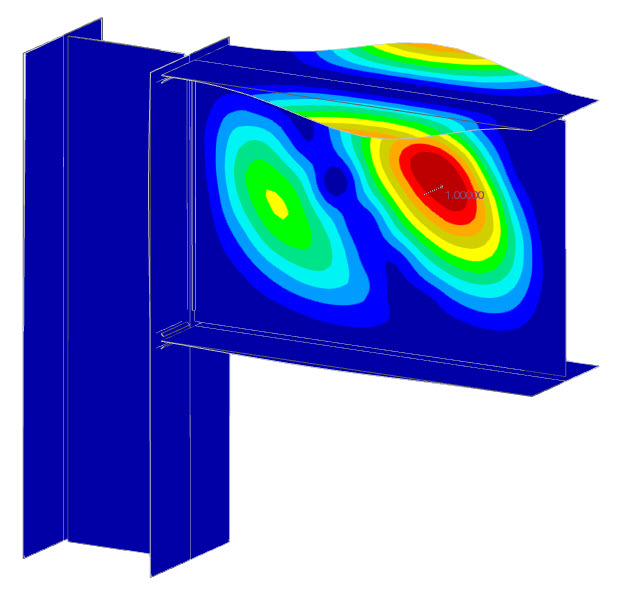
屈曲分析
“替代钢连接有限元模型”方法也适用于使用壳模型有限元分析进行钢板屈曲评估。为此,静力分析中使用的模型在一定程度上进行了调整,最终应用了“替代钢连接屈曲有限元模型”(“屈曲子模型”)。
“屈曲子模型”的更改设置如下:
- 所使用的所有材料均被认为是弹性的(杆和板料、螺栓模型的所有部分、焊缝替代面)。
模型通过强加节点变形在末端加载而非从全局结构模型中的力。此变形等同于连接荷载,但其使用可确保自由杆不会对稳定性分析结果产生负面影响。
- 默认情况下,屈曲子模型对静力分析使用“二阶(P-Δ)”分析类型,而稳定性分析则使用具有四个最低特征值的“特征值法(线性)”。
通过计算,模型提供所需数量的特征值及各自的临界荷载因子。用户负责判断钢连接的稳定性是否足够。
刚度分析
使用两个子模型来评定连接的刚度。这是主模型替代刚度有限元模型(刚度子模型)——一个细节化的壳模型,除荷载和支承外与用于静力分析的子模型相同——和辅助刚度有限元模型(辅助刚度子模型),用于考虑连接杆变形的影响。
“刚度子模型”的设计参数在刚度分析配置中管理。通过此设置,您可以选择“分析类型”(几何线性或二阶P-Δ),以及定义“最大迭代次数”和“荷载步骤数”。您还可以控制模型大小和网格设置,类似于在连接的应力-应变分析中适用的承载能力配置设置。更多的模型参数也从承载力配置中导入。
施加于两个子模型(刚度子模型和辅助刚度子模型)上的荷载组件与待分析的铰接刚度相对应。刚度针对连接中每个杆分别进行分析。分析的杆在末端被施以大小较小但方向为检验刚度S (SN+, SN-, SMy+, SMy-, SMz+, SMz-)的荷载,其它连接中的杆的末端被刚性固定。确定“初始刚度”的荷载大小取决于连接的每个杆的尺寸。
计算完成后,使用刚度子模型来确定分析杆每个末端的变形(旋转或位移)。从得到的变形中减去从辅助刚度子模型获得的变形以考虑连接的杆的影响。结果是根据荷载和变形计算的连接刚度。基于此刚度可将连接分类为“铰接的”、“可屈的”或“弯曲刚度的”。