W tym artykule opisano modelowanie ścieżki wirowej Karmana w programie RWIND.
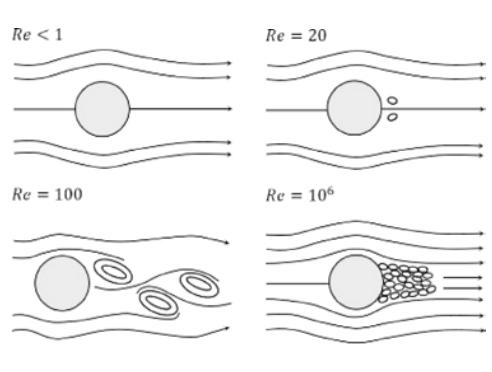
W przypadku niektórych zakresów liczb Reynoldsa za wąskimi, ale wysokimi obiektami tworzy się ulica wirów. Zwłaszcza w obszarach z dużą liczbą wysokościowców i tendencją do wąskich drapaczy chmur, wiry te mogą mieć wpływ na obciążenie wiatrem otaczających budynków. Poniżej przedstawiono tworzenie się wirów w funkcji liczby Reynoldsa zgodnie z [1].
Znana ulica wirowa rozwija się w oparciu o liczbę Reynoldsa wynoszącą około 100. Wraz ze wzrostem liczby przepływ staje się turbulentny. Do tej pory zadowalające wyniki osiągnięto tylko przy zbyt wysokim zakresie liczb Reynoldsa. Poniżej znajduje się przykład, gdzie Re = 10e7.
W związku z tym prędkość wlotowa musiała być ustawiona znacznie wyżej niż obliczono, aby wywołać pożądane zachowanie. Dokładną graniczną prędkość można określić teoretycznie, ale wymagałoby to wielu indywidualnych symulacji (nawet dla liniowo narastającego profilu wiatru), co zostało odrzucone ze względu na czas. Ponadto wydaje się, że częstotliwość wirowania nie odpowiada teorii. Ponieważ częstotliwość separacji zależy od liczby Strouhala, a tym samym od prędkości przepływu, zachowania tego można było oczekiwać.
Prawdopodobnie najważniejszym czynnikiem wpływającym na prawidłowe ukształtowanie ulicy wirowej jest gęstość siatki. W celu zaoszczędzenia zasobów, gęstość siatki w RWIND jest zmniejszana poprzez zwiększanie odległości od analizowanego obiektu w tunelu aerodynamicznym. To uproszczenie jest bardzo przydatne w przypadku pojedynczych budynków, ale utrudnia modelowanie ulicy wirów Kármána. W związku z tym sensowne jest na przykład zagęszczenie siatki, np. przekrój nad wysokością konstrukcji'na całej długości tunelu aerodynamicznego, zaczynając od wysokości konstrukcji'. Efekt takiego wygładzenia pokazano poniżej.
W kontekście niniejszej analizy nie uwzględniono, w jakim stopniu zagęszczenie siatki wpływa na końcowe naciski na sąsiednie budynki. Wymaga to dalszej analizy z wykorzystaniem przyszłego modelowania.
Dzięki dostosowanej kolorystyce i dopracowanej siatce powstał poniższy obraz. Lekko pochylony widok umożliwia lepsze rozróżnienie między różnymi odcieniami czerwieni.
Interesujący jest kierunek wektorów prędkości. Największa turbulencja, która znajduje się bezpośrednio za konstrukcją, wykazuje pożądany chaotyczny rozkład wektorów kierunkowych, jakiego można by oczekiwać w przypadku wiru. Jednak mniejsze wiry w większej odległości od konstrukcji nie wykazują takiego zachowania. Pomimo tego, że obraz bezwzględnego rozkładu prędkości może wskazywać w fałszywych kolorach, wiry są mniejsze, wszystkie wektory kierunku są zwrócone w kierunku dopływu. Z punktu widzenia mechaniki płynów takie zachowanie jest absurdalne, ale nie można zidentyfikować konkretnej przyczyny.
Dalsza optymalizacja ulicy wirowej byłaby możliwa dzięki ponownemu rozdrobnieniu siatki. Możliwe jest również, że nawet dokładniejsze udokładnienie mogłoby również skorygować anomalię wektorów kierunkowych. Odzwierciedla to jednak znacznie większe zapotrzebowanie na pamięć i moc obliczeniową. Zalecane jest jak najmniejsze zagęszczenie siatki, ale tak duże, jak to konieczne. Do tego celu najlepiej nadaje się górna jedna trzecia walca, zawierająca wystarczającą odległość od górnych węzłów.
Podsumowując, modelowana ulica wirowa wykazuje stosunkowo dobre wyniki w odniesieniu do prędkości, a tym samym profilu ciśnienia. W szczegółach, takich jak rozkład wektora kierunkowego i częstotliwość emisji, podejście przedstawione w tym artykule prawdopodobnie zawiedzie ze względu na ograniczenia samego solwera. Zaleca się powtórzenie tego obliczenia z najnowszymi wersjami RWIND.