Cet article décrit la modélisation d'une allée de tourbillons de Kármán dans RWIND.
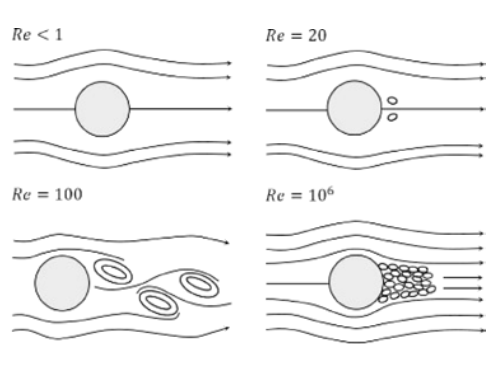
Pour certaines intervalles de nombres de Reynolds, une allée de tourbillons se forme derrière des objets étroits mais hauts. Ces tourbillons peuvent avoir un impact sur les charges de vent des bâtiments environnants, en particulier dans les zones avec de nombreux immeubles de grande hauteur, d'autant plus là où la tendance est aux gratte-ciel étroits. Voici la formation de tourbillons en fonction du nombre de Reynolds selon [1].
La célèbre allée de tourbillons se développe sur la base d'un nombre de Reynolds d'environ 100. Lorsque le nombre augmente, l'écoulement devient turbulent. Jusqu'à présent, des résultats satisfaisants n'ont été obtenus que dans une intervalle de nombres de Reynolds trop élevée. Ci-dessous, un exemple où Re = 107.
Par conséquent, la vitesse d'entrée a dû être réglée beaucoup plus élevée que prévu afin de déclencher le comportement souhaité. Une vitesse limite exacte pourrait être identifiée théoriquement, mais nécessiterait de nombreuses simulations individuelles (même pour un profil de vent croissant linéairement), ce qui a été rejeté pour des raisons de temps. De plus, la fréquence du tourbillonnement ne semble pas correspondre à la théorie. Étant donné que la fréquence de séparation dépend du nombre de Strouhal et donc de la vitesse d'écoulement, ce comportement était prévisible.
Le facteur d'influence le plus important pour la formation correcte d'une allée de tourbillons est probablement la densité de maillage. Afin d'économiser des ressources, la densité de maillage dans RWIND est réduite en augmentant la distance par rapport à l'objet analysé dans la soufflerie. Cette simplification est très utile pour les bâtiments individuels, mais rend plus difficile la modélisation de l'allée de tourbillons de Karman. Par conséquent, un raffinement de maillage est utile, par exemple, pour une section au-dessus de la hauteur de la structure sur toute la longueur de la soufflerie, en commençant par la profondeur de la structure. L'effet d'un tel raffinement est montré ci-dessous.
Dans le contexte de la présente analyse, il n'a pas été considéré dans quelle mesure un raffinement de maillage affecte les pressions ultimes sur les bâtiments environnants. Cela nécessite une analyse plus approfondie à l'aide d'une modélisation future.
L'image suivante est le résultat obtenu grâce à une coloration adaptée et un maillage raffiné. La vue légèrement inclinée permet de mieux distinguer les différentes nuances de rouge.
La direction des vecteurs de vitesse est intéressante. La plus grande turbulence, qui est directement derrière la structure, montre la distribution chaotique souhaitée des vecteurs directionnels comme on pourrait s'y attendre avec un vortex. Cependant, les tourbillons plus petits et plus éloignés de la structure ne présentent pas ce comportement. Bien que l'image en fausses couleurs de la distribution de vitesse absolue puisse indiquer des tourbillons plus petits, tous les vecteurs de direction pointent dans la direction de l'afflux. En termes de mécanique des fluides, ce comportement n'a pas de sens, mais une cause spécifique ne peut pas être identifiée.
Une optimisation supplémentaire de l'allée de tourbillon serait possible grâce à un maillage à nouveau raffiné. Il est également concevable qu'un raffinement encore plus fin puisse également corriger l'anomalie des vecteurs directionnels. Cependant, cela se traduit par des besoins en mémoire et en puissance de calcul nettement plus importants. Un raffinement de maillage aussi petit que possible mais aussi grand que nécessaire est recommandé. Le tiers supérieur du cylindre avec une distance suffisante aux nœuds supérieurs serait probablement le mieux adapté pour cela.
Dans l'ensemble, l'allée de tourbillons modélisée montre des résultats relativement bons en ce qui concerne la vitesse, et donc le profil de pression. Sur des points détaillés comme la distribution des vecteurs directionnels ainsi que la fréquence d'émission, l'approche présentée ici échoue probablement à cause des limites inhérentes au solveur lui-même. Il est conseillé de répéter ce calcul avec les dernières versions de RWIND.
[1] Image pour l'allée de tourbillons de Karman et le nombre de Reynolds