Este artigo descreve a modelação de um vórtice de von Kármán no RWIND.
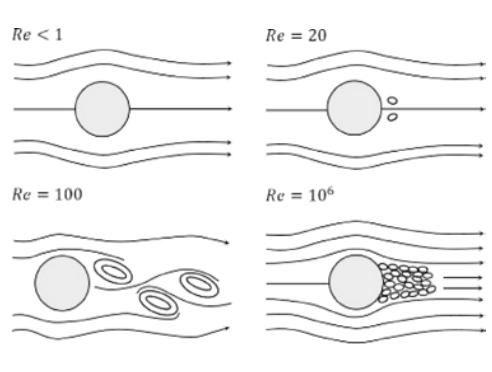
Para determinados intervalos de números de Reynolds, é formado vórtice por trás de objetos estreitos mas altos. Especialmente em áreas com muitos arranha-céus e com tendência para arranha-céus estreitos, estes vórtices podem ter um impacto nas cargas de vento dos edifícios circundantes. De seguida, é apresentada a formação de vórtices como uma função do número de Reynolds de acordo com [1].
A conhecida rua de vórtices desenvolve-se com base do número de Reynolds de cerca de 100. Quando o número aumenta, o fluxo torna-se turbulento. Até agora, só foram alcançados resultados satisfatórios num intervalo de números de Reynolds muito alto. Encontre um exemplo em que Re = 10e7 abaixo.
Por isso, foi necessário definir a velocidade de entrada muito mais alta do que a calculada de forma a desencadear o comportamento desejado. Pode ser identificada de forma teórica a velocidade limite exata, mas exigiria muitas simulações individuais (mesmo para um perfil de vento linearmente crescente), o que foi descartado por razões de tempo. Além disso, a frequência de libertação de vórtices não parece corresponder à teoria. Uma vez que a frequência de separação depende do número de Strouhal e, portanto, da velocidade do fluxo, era esperado este comportamento.
A densidade da malha é provavelmente, o fator de influência mais importante para a formação correta de um vórtice. De forma a poupar recursos, a densidade de malha no RWIND é reduzida através do aumento da distância ao objeto analisado no túnel de vento. Esta simplificação é muito útil para edifícios individuais, mas torna a modelação do vórtice de Kármán mais difícil. Por isso, faz sentido um refinamento de malha, por exemplo, de uma secção acima da altura da estrutura em todo o comprimento do túnel de vento, começando com a altura da estrutura. O efeito de tal refinamento é apresentado abaixo.
No contexto da presente análise, não foi considerado em que medida o refinamento da malha afeta as pressões últimas nos edifícios circundantes. Isto necessita de uma análise mais aprofundada utilizando modelação futura.
Devido a uma coloração adaptada e a uma malha refinada, obtém-se a seguinte imagem. A vista ligeiramente inclinada permite uma melhor distinção entre os diferentes tons de vermelho.
O que é interessante é a direção dos vetores velocidade. A turbulência maior, que se encontra diretamente por trás da estrutura, mostra a distribuição caótica desejada dos vetores direcionais, como seria de esperar com um vórtice. No entanto, vórtices mais pequenos a uma distância maior da estrutura não apresentam esse comportamento. Embora a imagem com cores falsas da distribuição de velocidades absolutas possa indicar vórtices menores, todos os vetores de direção apontam na direção do fluxo de entrada. Em termos da mecânica dos fluidos, este comportamento é absurdo, mas não pode ser idêntificada uma causa em específico.
Uma otimização adicional do vórtice seria possível atrvés de uma malha que é novamente refinada. É também concebível que um refinamento ainda mais fino possa corrigir a anomalia dos vetores direcionais. No entanto, isso reflete-se num requisito de memória e computação significativamente maior. Um refinamento da malha que é o mais pequeno possível, mas que seja o maior possivel dentro do que seria aconselhável. O terço superior do cilindro incluindo uma distância suficiente aos nós superiores seria provavelmente o mais adequado para isso.
Em suma, o vórtice modelado apresenta resultados relativamente bons no que diz respeito à velocidade e, consequentemente, ao perfil de pressão. Em detalhe, como a distribuição do vetor direccional e a frequência de emissão, a abordagem apresentada neste artigo provavelmente falha devido às limitações do próprio solucionador. É aconselhável repetir este cálculo com as versões mais recentes do RWIND.
.png?mw=350&hash=f79867dbf405d536638daef39ee25b113e6e540d)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
