V tomto příspěvku popisujeme modelování Kármánovy vírové stezky v programu RWIND.
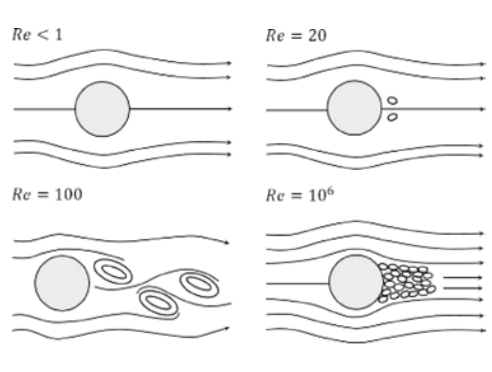
Pro určité rozsahy Reynoldsových čísel se za úzkými, vysokými objekty vytváří vírová stezka. Zejména v oblastech s mnoha výškovými budovami a s trendem štíhlých mrakodrapů mohou tyto víry ovlivnit zatížení větrem okolních budov. Následuje popis vzniku vírů v závislosti na Reynoldsově číslu podle [1].
Známá vírová stezka se začíná tvořit od Reynoldsova čísla okolo 100. Pokud se toto číslo zvýší příliš, stane se proudění turbulentním. Dosud bylo dosaženo uspokojivých výsledků pouze v případech, kdy bylo Reynoldsovo číslo příliš vysoké. Níže je uveden příklad pro Re = 10e7.
Pro dosažení požadovaného chování bylo nutné nastavit rychlost proudění mnohem vyšší než vypočítanou. Teoreticky by mohla být stanovena přesná mezní rychlost, ale to by vyžadovalo mnoho jednotlivých simulací (i s lineárně rostoucím profilem větru), od čehož bylo z časových důvodů upuštěno. Frekvence odtrhávání vírů se kromě toho nezdá být v souladu s teorií. Protože frekvence odtrhávání vírů závisí na Strouhalově čísle a tím i na vstupní rychlosti proudění, dalo se toto chování očekávat.
Pravděpodobně nejdůležitějším faktorem ovlivňující správné vytvoření vírové stezky je hustota sítě. Aby se ušetřila výpočetní náročnost, hustota sítě v programu RWIND se ve větrném tunelu snižuje s rostoucí vzdáleností od posuzovaného objektu. Toto zjednodušení je velmi užitečné pro modelování samostatných budov, ale ztěžuje modelování Kármánovy vírové stezky. Proto zde má smysl použít zahuštění sítě, například řezu přes výšku tělesa po celé délce větrného tunelu, počínaje hloubkou tělesa. Níže je ukázán vliv takového zahuštění.
V této studii nebylo zohledněno, do jaké míry má zahuštění sítě vliv na výsledné tlaky na okolní budovy. To bude zkoumáno v dalších studiích.
S upravenou barevnou škálou a se zhuštěnou sítí dostaneme následující obrázek. Mírně zešikmený pohled umožňuje lepší rozlišení mezi různými odstíny červené.
Zajímavý je přitom směr vektorů rychlosti. Největší turbulence přímo za tělesem vykazuje požadovaný chaotický průběh směrových vektorů tak, jak by se u víru dalo očekávat. Nicméně menší víry ve větší vzdálenosti od tělesa toto chování nevykazují. Obrázek absolutního rozdělení rychlostí ve špatných barvách sice naznačuje menší víry, všechny směrové vektory jsou ale ve směru proudění. Z hlediska mechaniky proudění je toto chování nesmyslné, konkrétní příčinu ale nelze určit.
Další optimalizace vírové stezky by byla možná s ještě jemnější sítí. Lze si také představit, že ještě jemnější síť by mohla také opravit anomálii směrových vektorů. To ovšem s sebou nese podstatně vyšší nároky na paměť a výpočetní výkon. Z toho hlediska by bylo vhodné použít co nejmenší zahuštění sítě. Nejlépe by se asi pro zahuštění hodila oblast ve tvaru horní třetiny válce s dostatečnou vzdáleností od horních uzlů.
Závěrem lze říci, že modelovaná vírová stezka vykazuje relativně dobré výsledky s ohledem na rychlost a tím i tlakový profil. V tak detailních bodech, jako je rozdělení směrových vektorů a emisní frekvence, zde prezentovaný přístup pravděpodobně není úspěšný kvůli omezením samotného řešiče. Tento výpočet by bylo vhodné opakovat u novějších verzí programu RWIND.
[1] Obrázek pro Kármánovu vírovou stezku a Reynoldsovo číslo