16489x

001625

Dipl.-Ing. (FH) Gerhard Rehm

2020-02-28

Instabilità flesso-torsionale nelle strutture in legno | Metodo di analisi

Le aste inflesse sottili con un rapporto elevato h/w e caricate parallelamente all'asse minore tendono ad avere problemi di stabilità. Ciò è dovuto alla inflessione nel corrente compresso.

La trave ha uno spostamento laterale con rotazione simultanea (vedi Figura 01). Questo è chiamato instabilità flesso-torsionale o instabilità laterale. Simile all'instabilità flessionale, dove un'asta si deforma improvvisamente quando viene raggiunto il carico di Eulero, il corrente compresso si sposta da un carico critico di instabilità laterale durante l'instabilità flesso-torsionale. Ciò si traduce in un momento flettente critico M_crit, che si traduce in una tensione critica per instabilità laterale σ_crit.

Instabilità laterale di una trave a campata singola

1 Kippen eines Einfeldträgers

Simboli utilizzati:

Kippen eines Einfeldträgers	Lunghezza trave
E	Modulo elastico
Kippen eines Einfeldträgers	Modulo di taglio
i_Z	Secondo momento dell'area intorno all'asse debole
i_T	Costante torsionale
I_ω	costante di ingobbamento
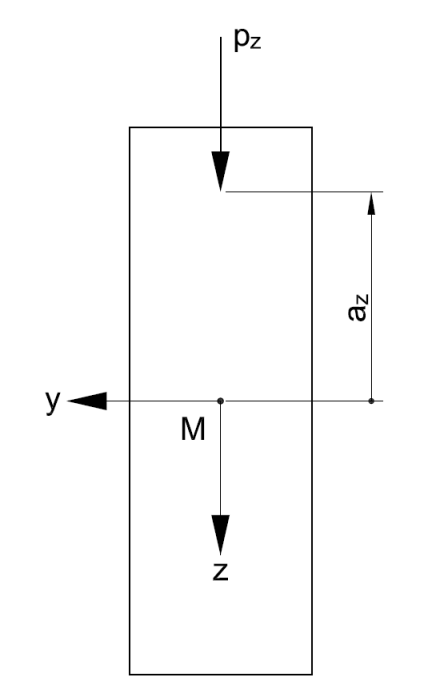
a_z	Distanza dell'applicazione del carico dal centro di taglio
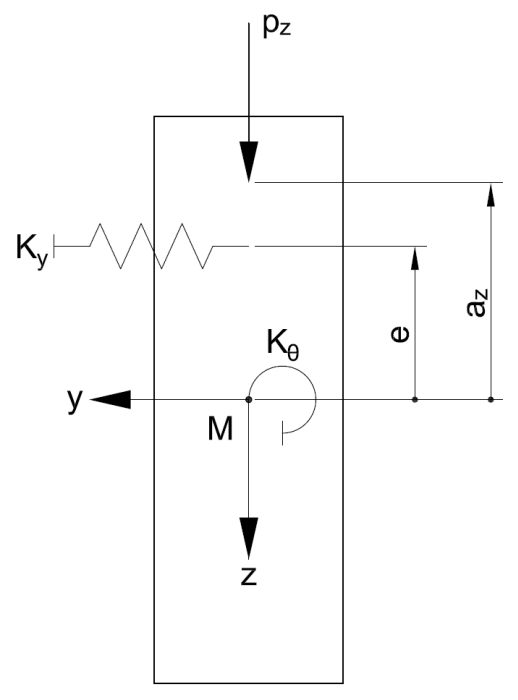
e	Distanza della fondazione elastica dell'asta dal centro di taglio
K_{Kippen eines Einfeldträgers}	molla rotazionale elastica sul vincolo esterno in Nmm
K_θ	vincolo rotazionale elastico in N
K_y	fondazione dell'asta elastica in N/mm²

Determinazione analitica di M_crit

Per determinare il momento flettente in cui una trave diventa instabile, l'ingegnere può utilizzare le soluzioni analitiche della letteratura, ma queste sono limitate nella loro applicazione. In [1], la seguente equazione è derivata per una trave a campata singola con vincoli laterali e torsionali e incernierata su entrambi i lati, con un momento flettente costante e applicazione del carico al centro di taglio.

M_{crit} = \frac{π}{L} \cdot \sqrt{{EI}_{z} \cdot {GI}_{T} \cdot (1 + \frac{{EI}_{ω}}{{GI}_{T}} \cdot \frac{π^{2}}{L^{2}})}

Momento critico

Nel caso di sezioni trasversali non libere di ingobbamento (ad esempio, una sezione trasversale rettangolare stretta in una costruzione in legno), la rigidezza di ingobbamento può essere impostata su zero; quindi, la parte tra parentesi è omessa.

M_{crit} = \frac{π}{L} \cdot \sqrt{{EI}_{z} \cdot {GI}_{T}}

Momento critico senza rigidezza di ingobbamento

Poiché ci sono molti più casi nell'analisi strutturale rispetto a quelli sopra menzionati, sono stati introdotti coefficienti di correzione per tenere conto, ad esempio, delle distribuzioni dei momenti devianti, delle situazioni dei vincoli e di una diversa applicazione del carico. Per questo, la lunghezza della trave viene modificata con i coefficienti e risulta in una lunghezza efficace l_ef. Questo è descritto in [2], tra l'altro, come segue.

l_{ef} = \frac{L}{a_{1} \cdot [1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{{EI}_{z}}{{GI}_{T}}}]}

lunghezza di libera inflessione

a_z è la distanza dell'applicazione del carico dal centro di taglio.

Descrizioni sulla sezione trasversale rettangolare

2 Bezeichnungen am Rechteckquerschnitt

Se il carico agisce sul lato inferiore della trave, si deve considerare una_z con segni negativi. I coefficienti a₁ e a₂ sono mostrati nell'immagine 03.

3 Fattori di instabilità laterale

I diversi sistemi devono essere intesi come segue:

Trave a campata singola con vincoli laterali e torsionali e incernierata su entrambi i lati
Trave vincolata
Sbalzo con vincolo laterale e torsionale all'estremità libera
Trave fissata su entrambi i lati
Trave a campata singola con vincolo su un lato
Trave a due campate
Trave continua con vincolo laterale e torsionale - campata interna
Trave continua con vincolo laterale e torsionale - campata esterna

Le norme suggeriscono il progetto di instabilità laterale secondo il metodo dell'asta equivalente. È necessario calcolare il momento critico con i valori del quantile del 5% delle rigidezze. Pertanto, i seguenti risultati per le strutture in legno:

M_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{z} \cdot G_{0.05} \cdot I_{T}}}{l_{ef}}

Momento critico per strutture in legno

La tensione critica di flessione risulta in:

σ_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{z} \cdot G_{0.05} \cdot I_{T}}}{l_{ef} \cdot W_{y}}

Tensione flettente critica

Se si desidera considerare una molla rotazionale elastica (ad esempio, risultante dalla flessibilità del vincolo laterale e torsionale) sul vincolo esterno, un vincolo rotazionale elastico (ad esempio, da una lamiera trapezoidale) o un vincolo esterno elastico dell'asta (ad esempio , dai controventi), è possibile estendere l'equazione precedente come segue: [2].

l_{ef} = \frac{L}{a_{1} \cdot [1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{{EI}_{z}}{{GI}_{T}}}]} \cdot \frac{1}{α \cdot β}

Lunghezza efficace considerando la molla rotazionale elastica, il vincolo rotazionale o il vincolo esterno elastico dell'asta

dove

α = \sqrt{\frac{1}{1 \frac{3.5 \cdot {GI}_{T}}{K_{G} \cdot L}}}

β = \sqrt{(1 \frac{K_{y} \cdot L^{4}}{{EI}_{z} \cdot π^{4}}) \cdot (1 \frac{(K_{θ} e^{2} \cdot K_{y}) \cdot L^{2}}{{GI}_{T} \cdot π^{2}})} + \frac{e \cdot K_{y} \cdot L^{3}}{\sqrt{{EI}_{z} \cdot {GI}_{T}} \cdot π^{3}}

Calcolo di α e β

Descrizioni sulla sezione trasversale rettangolare con molle elastiche

4 Bezeichnungen am Rechteckquerschnitt mit elastischen Federn

Se la molla rotazionale K_G al vincolo esterno è considerata come infinitamente rigida, il risultato α = 1. Il vincolo rotazionale elastico K_Θ non è generalmente considerato nelle costruzioni in legno, poiché non ci sono studi. Pertanto, il parametro K_Θ è incluso nell'equazione con il valore 0. La fondazione elastica dell'asta elastica K_y, risultante da un controvento o da un pannello di taglio, ha un effetto favorevole sul comportamento di instabilità laterale di una trave. Tuttavia, si noti che l'equazione precedente ha un'applicazione limitata. A rigor di termini, è valido solo se c'è una inflessione in un grande arco sinusoidale. Se la fondazione dell'asta è troppo rigida, questo non è più dato perché la forma modale ha diversi archi lungo la trave. Al momento non c'è una definizione di quando la formula estesa con α e β diventa non valida.

Trovare la soluzione per tali problemi agli autovalori in modo abile sarà descritto con diversi esempi nel prossimo articolo.

Knowledge Base

KB 001625 | Instabilità flesso-torsionale nelle strutture in legno | Teoria

Autore

Il signor Rehm è responsabile dello sviluppo di prodotti per strutture in legno e fornisce supporto tecnico ai clienti.

Link

Software per strutture in legno

Bibliografia

Timoshenko, S., & Gere, JM M.; Theory of Elastic Stability, 2. Auflage. New York: McGraw-Hill, 1961
Appendice nazionale - Eurocodice 5: Progettazione di strutture in legno - Parte 1-1: Generale - Regole e regole comuni per gli edifici; DIN EN 1995-1-1/NA:2013-08

;

Instabilità flesso-torsionale nelle strutture in legno | Metodo di analisi

Determinazione analitica di Mcrit

Determinazione analitica di M_crit