Encurvadura por flexão-torção em estruturas de madeira | Teoria

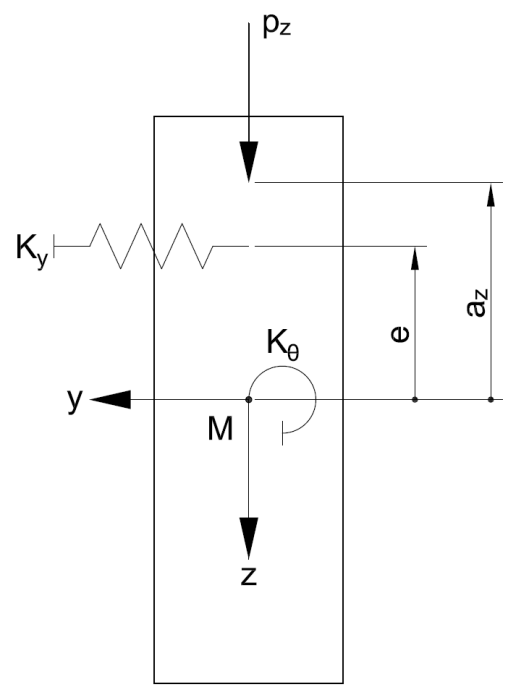
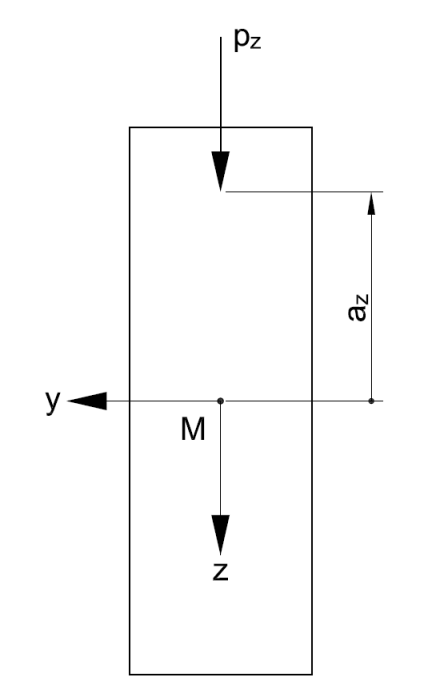
A viga contém um deslocamento lateral com rotação em simultâneo (ver Figura 01). Isso é designado como encurvadura por flexão-torção ou encurvadura por flexão Semelhante à encurvadura por flexão, na qual uma barra encurva repentinamente quando é atingida a carga de encurvadura de Euler, o banzo de compressão diverge de uma carga crítica durante a encurvadura por flexão-torção. Isto resulta num momento de flexão crítico M_crit, o que resulta numa tensão de flexão crítica σ_crit.

Kippen eines Einfeldträgers

Símbolos utilizados:
L = Comprimento da viga
E ... Módulo de Young
G ... módulo de corte
I_Z ... momento de inércia sobre o eixo menor
I_t ... Constante de torção
I_ω ... Resistência ao empenamento
a_z ... distância da aplicação de carga a partir do centro de corte
e ... distância da barra de fundação elástica a partir do centro de corte
K_G ... mola de torção elástica sobre apoio em Nmm
K_Θ ... restrição de rotação elástica em N
k_Y ... barra de fundação elástica em N/mm²

Determinação analítica de M_crit

Para determinar o momento de flexão sob o qual uma viga se torna instável, as soluções analíticas estão disponíveis para o engenheiro na literatura, mas estas são limitadas na sua aplicação. Em [1], a equação seguinte é derivada para uma viga de vão único com restrições à flexão e torção e articuladas nos dois lados com um momento de flexão constante e uma aplicação de carga no centro de corte.

No caso de secções com restrições ao empenamento (por exemplo, uma secção retangular estreita em construções de madeira), a resistência ao empenamento pode ser definida como zero e assim a parte entre parênteses é omitida.

Uma vez que existem muito mais casos em engenharia estrutural do que os mencionados acima, foram introduzidos fatores de correção para ter em conta, por exemplo, distribuições de momentos divergentes, diferentes situações de apoio e aplicações de carga. Para isso, é alterado o comprimento da viga com os fatores e resulta num comprimento efetivo l_ef. Isto é descrito em [2], entre outros, como se segue.

a_z é a distância da aplicação da carga ao centro de corte.

Bezeichnungen am Rechteckquerschnitt

Se a carga atua sobre a parte inferior da viga, deve ser considerado a_z com sinais negativos. Os coeficientes a₁ e a₂ são apresentados na Figura 03.

Coeficientes da encurvadura por flexão

Os diferentes sistemas devem ser entendidos do seguinte modo:

1. Viga de vão único com restrições à flexão e torção e articulada nos dois lados
2. Viga restringida
3. Consola com restrição à flexão-torção na extremidade livre
4. Viga apoiada nos dois lados
5. Viga de um vão com restrição de um lado
6. Viga de dois vãos
7. Viga contínua com restrição à flexão e torção - vão interior
8. Viga contínua com restrição à flexão e torção - vão exterior

Nas normas sugerem o dimensionamento da encurvadura por flexão de acordo com o método de barra equivalente. O utilizador tem de calcular momento crítico com os valores de 5% da rigidez. Portanto, os seguintes resultados para construção em madeira:

A tensão de flexão crítica resulta em:

Se pretende considerar uma mola de rotação elástica (por exemplo resultante da flexibilidade da restrição à flexão-torção) no apoio, uma restrição à rotação elástica (por exemplo a partir da chapa trapezoidal) ou uma fundação elástica de barra elástica (por exemplo contraventamento), pode prolongar a equação anterior do seguinte modo [2].

Bezeichnungen am Rechteckquerschnitt mit elastischen Federn

Se a mola de rotação K_G no apoio é considerada como infinitamente rígida, o resultado é α = 1. A restrição rotacional elástica K_Θ geralmente não é considerada nas estruturas de madeira, uma vez que não existem estudos. Assim, o parâmetro K_Θ é incluído na equação com o valor 0. A barra elástica de fundação elástica K_y, resultante de um contraventamento ou um painel de corte, tem um efeito favorável no comportamento da encurvadura por flexão de uma viga. No entanto, deve ser observado que a equação anterior é limitada na sua aplicação. A rigor, isso só é válido se ocorrer uma deformação num grande arco sinusoidal. Se a barra de fundação é muito rígida, isto não é mais o caso, porque a forma de modo tem vários arcos ao longo da viga. Atualmente, não existe uma definição de quando a fórmula prolongada com α e β se torna inválida.

A forma como resolver esses problemas de valor próprio de forma qualificada é descrita com diferentes exemplos no próximo artigo.

• Encurvadura por flexão-torção em estruturas de madeira | Exemplos 1
• Encurvadura por flexão-torção em estruturas de madeira | Exemplos 2