Балка подвергается боковому смещению одновременно с вращением (см. рисунок 01). Речь идет о продольном изгибе с кручением или боковом выпучивании. Подобно упругому выпучиванию, когда стержень внезапно выгибается при достижении нагрузки Эйлера, при боковом выпучивании сжатый пояс выгибается от критической поперечной нагрузки. Это приводит к возникновению критического изгибающего момента Mcrit, который способствует возникновению критического напряжения при продольном изгибе σcrit.
Используемые символы:
| Длина балки | |
| E | модуль упругости |
| модуль сдвига | |
| iZ | Момент инерции вокруг оси минимальных моментов |
| IT | момент инерции при кручении |
| Iω | Сопротивление депланации |
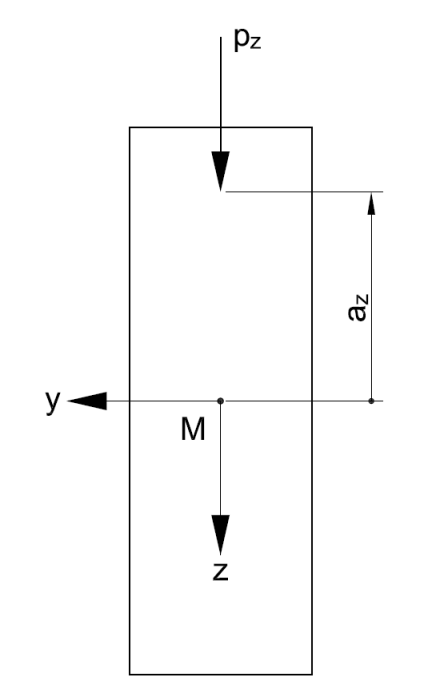
| az | Отступ точки приложения нагрузки от центра сдвига |
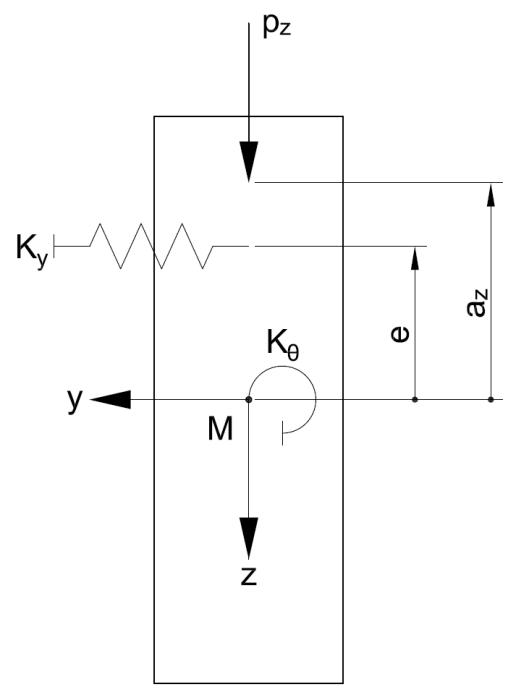
| e | Oтступ упругого основания стержня от центра сдвига |
| K | упругая торсионная пружина на опоре в Нмм |
| Kθ | упругое торсионное основание в Н |
| Ky | упругое основание стержня в Н/мм² |
Аналитический расчет Mcrit
Для того, чтобы найти значение изгибающего момента, при котором балка теряет устойчивость, проектировщик может применить аналитические решения из специальной литературы, однако существуют определенные ограничения для их применения. В [1] для однопролетной балки на шарнирных опорах с обеих сторон и с боковым и торсионным защемлением, у которой изгибающий момент постоянен, а нагрузка приложена в центре сдвига, приведено следующее уравнение.
В случае свободно депланирующих сечений (например, узкого прямоугольного сечения в деревянной конструкции), жесткость на депланацию может быть установлена равной нулю, и, таким образом, часть уравнения в скобках можно опустить.
Поскольку в расчетах конструкций встречается гораздо больше случаев, чем наш случай, описанный выше, были введены поправочные коэффициенты для учета, например, расходящихся эпюр моментов, условий опирания и иных условий приложения нагрузки. Поэтому длина балки изменяется с помощью коэффициентов и в результате мы получим полезную длину lef. Это описано в [2] следующим образом.
при этом az - отступ точки приложения нагрузки от центра сдвига.
Если нагрузка приложена к нижней стороне балки, то в расчете необходимо учитывать az со знаком минус. Коэффициенты a1 и a2 можно найти на рисунке 03.
Различают следующие системы:
- Однопролетная балка на шарнирных опорах с обеих сторон и с боковым и торсионным защемлением
- Защемленная балка
- Консоль с вильчатой опорой на свободном конце
- Балка, защемленная с обеих сторон
- Однопролетная балка с защемлением с одной стороны
- Двухпролетная балка
- Неразрезная балка с вильчатой опорой - внутренний пролет
- Неразрезная балка с вильчатой опорой - наружный пролет
В нормах предлагается выполнять расчет потери устойчивости при изгибе и кручении по методу замены связей. При этом критический момент рассчитывается с помощью 5%-ного квантиля значений жесткости. Таким образом, для деревянной конструкции мы получим:
Критическое напряжение при изгибе равно:
Если требуется учесть упругую торсионную пружину (например, возникающую в результате гибкости вильчатого опирания) на опоре, упругое поворотное основание (например, из профлиста) или упругое основание стержня (например, из связей), предыдущее уравнение можно расширить следующим образом: {%><#Refer [2]]].
Где:
Если поворотная пружина KG в опоре считается бесконечно жесткой, то мы получим α = 1. Упругое поворотное ограничение KΘ в деревянных конструкциях, как правило, не учитывается, так как для этого не требуется никаких исследований. Таким образом, параметр KΘ вводится в уравнение со значением 0. Упругое основание стержня Ky, возникающее в результате связи или сдвигового поля, оказывает благоприятное воздействие на характеристики бокового выпучивания балки. При этом необходимо обратить внимание на то, что предыдущее уравнение имеет ограничения в применении. Строго говоря, формула действительна только в случае прогиба по большой синусоидальной дуге. Если основание стержня слишком жесткое, то мы не получим, поскольку собственная форма вдоль балки содержит несколько дуг. В настоящее время не существует определения, с какого момента расширенная формула с α и β теряет силу.
Как грамотно решить подобную проблему собственных значений, мы покажем на различных примерах в нашей следующей статье.