16704x

001625

Dipl.-Ing. (FH) Gerhard Rehm

2020-02-28

Zwichrzenie w konstrukcjach drewnianych | Metoda analizy

W przypadku smukłych belek zginających o dużym stosunku h/w, obciążonych w kierunku słabej osi bezwładności, występują problemy ze statecznością. Wynika to z ugięcia pasu ściskanego.

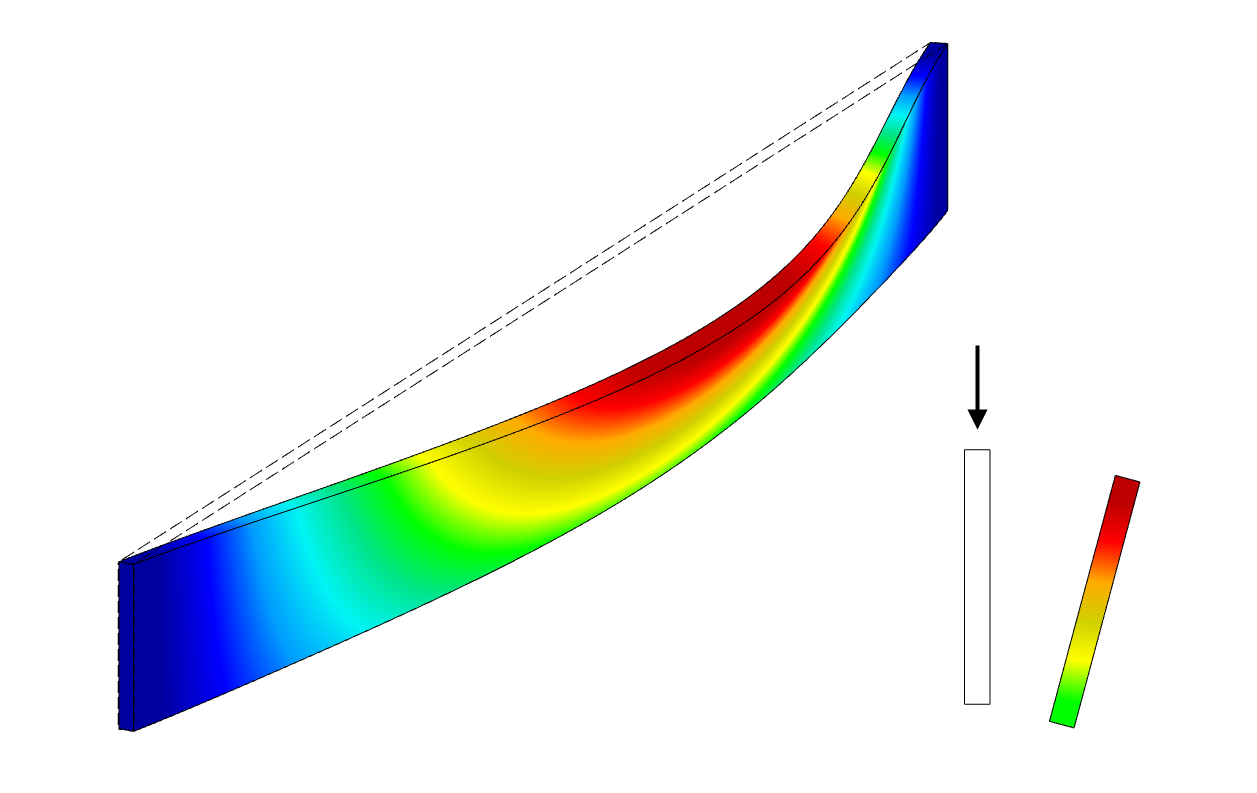
Belka ulega przemieszczeniu bocznemu z jednoczesnym obrotem (patrz Rysunek 01). Nazywa się to wyboczeniem giętno-skrętnym. Podobnie jak w przypadku wyboczenia giętnego, w którym pręt wybrzusza się nagle po osiągnięciu siły krytycznej Eulera, podczas wyboczenia giętno-skrętnego pas ściskany przesuwa się pod wpływem krytycznego obciążenia wyboczeniowego. Skutkuje to powstaniem krytycznego momentu zginającego M_kry , który powoduje naprężenie krytyczne przy wyboczeniu giętnym σ_kryt.

1 Kippen eines Einfeldträgers

Zastosowane symbole:

[CONTACT.E-MAIL-SALUTATION]	Długość belki
E	moduł sprężystości
[SCHOOL.NUMBEROFSINGLEUSERLICENCES]	Moduł ścinania
I_Z	moment bezwładności wokół osi drugorzędnej
I_T	Moment bezwładności przy skręcaniu swobodnym
I_ω	stała deplanacji
a_z	odległość przyłożenia obciążenia od środka ścinania
e	odległość sprężystej podpory pręta od środka ścinania
K_{[SCHOOL.NUMBEROFSINGLEUSERLICENCES]}	sprężyna obrotowa na podporze w Nmm
K_θ	sprężyste utwierdzenie obrotu w N
K_y	sprężyste podparcie pręta w N/mm²

Analityczne oznaczenie M_kryt

Aby określić moment zginający, przy którym belka staje się niestabilna, inżynier może wykorzystać rozwiązania zaczerpnięte z literatury, ale ich zastosowanie jest ograniczone. W [1] dla belki jednoprzęsłowej z utwierdzeniami bocznymi i skrętnymi, połączonej przegubowo po obu stronach ze stałym momentem zginającym i przyłożeniem obciążenia w środku ścinania, wyprowadzono następujące równanie.

M_{crit} = \frac{π}{L} \cdot \sqrt{{EI}_{z} \cdot {GI}_{T} \cdot (1 + \frac{{EI}_{ω}}{{GI}_{T}} \cdot \frac{π^{2}}{L^{2}})}

Moment krytyczny

W przypadku przekrojów, które nie mogą ulec deplanacji (na przykład wąski prostokątny przekrój w konstrukcji drewnianej), sztywność wycinkowa można ustawić jako równą zero, a tym samym pominąć część w nawiasach.

M_{crit} = \frac{π}{L} \cdot \sqrt{{EI}_{z} \cdot {GI}_{T}}

Moment krytyczny bez sztywności deplanacyjnej

Ponieważ w analizie statyczno-wytrzymałościowej jest znacznie więcej przypadków obciążenia i podparcia niż te wymienione powyżej, wprowadzono współczynniki korekcyjne w celu uwzględnienia na przykład różnych rozkładów momentów, sytuacji podporowych i innego układu obciążenia. W tym celu długość belki jest modyfikowana współczynnikami i daje efektywną długość l_ef . Jest to opisane między innymi w [2] poniżej.

l_{ef} = \frac{L}{a_{1} \cdot [1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{{EI}_{z}}{{GI}_{T}}}]}

długość efektywna

a_z jest odległością przyłożenia obciążenia od środka ścinania.

2 Bezeichnungen am Rechteckquerschnitt

Jeżeli obciążenie działa na dolną stronę belki, wartość a_z należy użyć w powyższym wzorze ze znakami ujemnymi. Współczynniki a₁ i a₂ pokazano na rysunku 03.

3 Współczynniki korekcyjne dla wyboczenia giętnego

Poszczególne układy konstrukcyjne należy rozumieć w następujący sposób:

Przegubowa belka jednoprzęsłowa z podparciami bocznymi i skrętnymi
Belka utwierdzona
Belka utwierdzona z podparciem bocznym i skrętnym na wolnym końcu
Belka zamocowana po obu stronach
Belka jednoprzęsłowa z utwierdzeniem po jednej stronie
belka dwuprzęsłowa
Belka ciągła z utwierdzeniem bocznym i skrętnym - przęsło pośrednie
Belka ciągła z utwierdzeniem bocznym i skrętnym - przęsło skrajne

Normy sugerują wymiarowanie wyboczenia bocznego według metody pręta równoważnego. Moment krytyczny należy obliczyć korzystając z 5% kwantyli sztywności. Tak więc dla konstrukcji drewnianych o przekroju prostokątnym otrzymuje się następujący wynik:

M_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{z} \cdot G_{0.05} \cdot I_{T}}}{l_{ef}}

Moment krytyczny w konstrukcjach drewnianych

Krytyczne naprężenia przy zginaniu:

σ_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{z} \cdot G_{0.05} \cdot I_{T}}}{l_{ef} \cdot W_{y}}

Krytyczne naprężenie przy zginaniu

Jeżeli na podporach ma zostać uwzględniona sprężyna obrotowa (na przykład wynikająca z podatności utwierdzenia bocznego i skrętnego), sprężyste utwierdzenie obrotowe (na przykład wynikające z blachy trapezowej) lub sprężyste podłoże pręta (na przykład , ze stężeń) poprzednie równanie można rozszerzyć w następujący sposób: [2].

l_{ef} = \frac{L}{a_{1} \cdot [1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{{EI}_{z}}{{GI}_{T}}}]} \cdot \frac{1}{α \cdot β}

Długość efektywna z uwzględnieniem sprężystej sprężyny obrotowej, ograniczenia obrotu lub sprężystego podłoża pręta

Gdzie

α = \sqrt{\frac{1}{1 \frac{3.5 \cdot {GI}_{T}}{K_{G} \cdot L}}}

β = \sqrt{(1 \frac{K_{y} \cdot L^{4}}{{EI}_{z} \cdot π^{4}}) \cdot (1 \frac{(K_{θ} e^{2} \cdot K_{y}) \cdot L^{2}}{{GI}_{T} \cdot π^{2}})} + \frac{e \cdot K_{y} \cdot L^{3}}{\sqrt{{EI}_{z} \cdot {GI}_{T}} \cdot π^{3}}

Obliczanie α i β

4 Bezeichnungen am Rechteckquerschnitt mit elastischen Federn

Jeżeli sprężyna obrotowa K_G na podporze jest uznana za nieskończenie sztywną, wynik α = 1. Ze względu na brak badań, sprężyste utwierdzenie obrotu K_Θ zazwyczaj nie jest uwzględniane w konstrukcjach drewnianych. Tym samym parametr K_Θ zostaje uwzględniony w równaniu i przyjmuje wartość 0. Sprężyste podparcie sprężyste pręta K_y, wynikające ze stężenia lub panelu usztywniającego, ma korzystny wpływ na wyboczenie giętne belki. Należy jednak pamiętać, że poprzednie równanie ma ograniczone zastosowanie. Ściśle mówiąc, jest ono prawidłowe tylko w przypadku wygięcia w postaci dużego łuku sinusoidalnego. Zbyt sztywne podparcie prętowe nie jest już uwzględniane, ponieważ kształt postaci wyboczeniowej ma kilka łuków wzdłuż belki. Obecnie nie ma definicji, kiedy wzór rozszerzony zawierający α i β staje się nieaktualny.

Jak umiejętnie rozwiązać takie problemy z wartością własną, pokażemy na różnych przykładach w kolejnym artykule.

Baza informacji

KB 001625 | Zwichrzenie w konstrukcjach drewnianych | Teoria

Autor

Pan Rehm jest odpowiedzialny za rozwój produktów do konstrukcji drewnianych i zapewnia wsparcie techniczne dla klientów.

Odnośniki

Oprogramowanie statyczne do konstrukcji drewnianych

Odniesienia

Timoshenko, S. & Gere, JM M.; Theory of Elastic Stability, 2. Auflage. New York: McGraw-Hill, 1961
Załącznik krajowy - Eurokod 5: Projektowanie konstrukcji drewnianych - Część 1-1: Ogólne - Reguły ogólne i reguły dla budynków; DIN EN 1995‑1-1/NA:2013-08

;

Zwichrzenie w konstrukcjach drewnianych | Metoda analizy

Analityczne oznaczenie Mkryt

Analityczne oznaczenie M_kryt