Volver a la base de datos de conocimientos

13792x

001629

Sonja von Bloh, M.Sc.

2020-03-02

Cálculo de una sección en C de pared delgada conformada en frío según EN 1993-1-3

Utilice la ampliación del módulo RF-/STEEL Cold-Formed Sections para realizar cálculos del estado límite último de secciones conformadas en frío según EN 1993-1-3 y EN 1993-1-5. Además de las secciones conformadas en frío de la base de datos de las secciones, también puede calcular las secciones generales realizadas en SHAPE-THIN.

En el siguiente ejemplo del Anuario de estructuras de acero 2009 [3], el cálculo de la sección para una viga de vano simple con una sección en C conformada en frío de pared delgada se realiza bajo carga del esfuerzo normal. La sección en C se modela en SHAPE-THIN y luego se calcula en RF-/STEEL Cold-Formed Sections.

Sistema

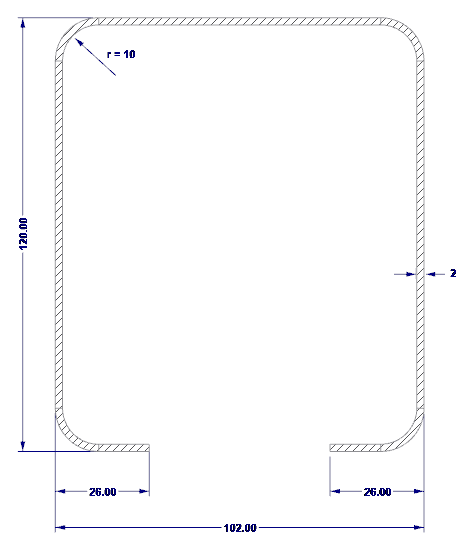
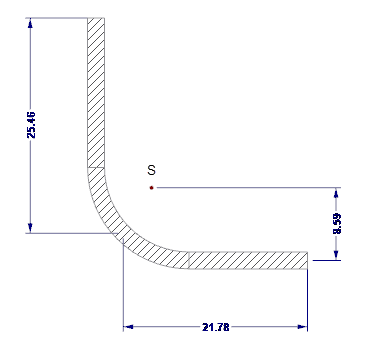
El sistema y la carga se muestran en la figura 01.

1 Sistema y carga (dimensiones en mm, fuerza en kN)

Material

S 355 EN 10025-2
E = 210,000 N/mm²
G = 80,769 N/mm²
ν = 0,3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1,00 (cálculo según CEN)

Dimensiones externas

Las dimensiones externas de la sección se muestran en la figura 02.

2 Außenabmessungen des Querschnitts in mm

H = 102 mm (altura del alma)
b = 120 mm (ancho del cordón)
c = 26 mm (longitud del labio)
t = 2 mm (espesor del núcleo de acero)

Anchuras planas teóricas

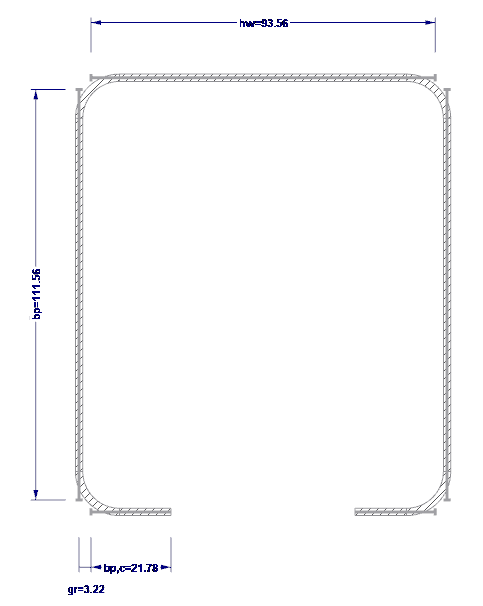
Las anchuras planas teóricas se determinan según [1], 5.1. Las anchuras planas teóricas se muestran en la figura 03.

3 Anchuras planas teóricas en mm

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

Anchuras planas teóricas

Comprobación de la relación anchura-espesor

Las relaciones anchura-espesor se comprueban según [1], 5.2(1).

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

Se cumplen las relaciones anchura-espesor.

Comprobación de las dimensiones de los rigidizadores

Las dimensiones del rigidizador se comprueban según [1], 5.2(2).
0,2 ≤ c/b = 26/120 = 0,22 ≤ 0,6

Los labios se pueden aplicar como rigidizadores.

Comprobación del ángulo entre el rigidizador y el elemento plano

El ángulo entre el rigidizador y el elemento plano es de 90° dentro de los límites de 45° y 135° mencionados en [1], 5.5.3.2(1).

Determinación de la sección eficaz

Para secciones de acero que no están sujetas a una doble simetría y que están sujetas a compresión, la posición del centro de gravedad de la sección eficaz se desplaza en comparación con la sección bruta. El esfuerzo de compresión externo que actúa centralmente en la sección bruta ahora actúa excéntricamente en la sección eficaz y se crea un momento flector adicional. Según [1], se deben tener en cuenta los momentos adicionales resultantes del desplazamiento del centro de gravedad. Posteriormente, además de la sección eficaz para una tensión de compresión pura, se debe determinar la sección eficaz para la tensión de flexión pura.

Determinación de la sección eficaz bajo compresión pura

Según [2], 4.4 (2), el coeficiente da como resultado:

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

Coeficiente ε

Alma

Según [2], tabla 4.1, el valor de pandeo da como resultado:

k_{σ} = 4

coeficiente de pandeo transversal o de alabeo

Según [2], 4.4 (2), la esbeltez de pandeo da como resultado:

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Esbeltez de pandeo del alma

La relación de esbeltez es mayor que el valor límite 0,673 según [2], 4,4(2). Por lo tanto, se requiere una reducción.

Según [2], 4.4 (2), el coeficiente de reducción da como resultado:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

Coeficiente de reducción para el alma

Según [2], tabla 4.1, la altura eficaz del alma resulta de [2], tabla 4.1 en:

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

Altura eficaz del alma

Ala con rigidizador de borde

En el primer paso, se determina una primera aproximación de la sección eficaz del rigidizador con la hipótesis de que la rigidez del borde actúa como un apoyo empotrado y con σ_com,Ed = f_yb / γ_M0.

Ala

Según [2], tabla 4.1, el valor de pandeo da como resultado:

k_{σ} = 4

coeficiente de pandeo transversal o de alabeo

Según [2], 4.4 (2), la esbeltez de pandeo da como resultado:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Esbeltez de pandeo del ala

La relación de esbeltez es mayor que el valor límite 0,673 según [2], 4,4(2). Por lo tanto, se requiere una reducción.

Según [2], 4.4 (2), el coeficiente de reducción da como resultado:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

Coeficiente de reducción para el ala

Según [2], tabla 4.1, la anchura eficaz del ala da como resultado:

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

Anchura eficaz del ala

rigidizador de borde

Según [1], 5.5.3.2 (5), el valor de pandeo da como resultado:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

valor de pandeo del rigidizador de borde

Según [2], 4.4 (2), la esbeltez de pandeo da como resultado:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Esbeltez de pandeo del rigidizador de borde

La relación de esbeltez es menor que el valor límite 0,748 según [1], 4,4(2). Por lo tanto, no es necesaria ninguna reducción, es decir: ρ = 1,0.

La primera aproximación de la anchura eficaz resulta de [1], ec. 5.13a para:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Primera aproximación de la anchura eficaz

En el segundo paso, el coeficiente de reducción para la inestabilidad de la forma de la sección se determina utilizando la primera aproximación eficaz de la sección, teniendo en cuenta la rigidez elástica a traslación.

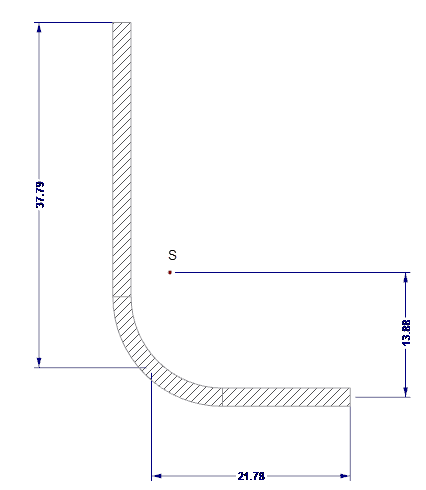
Los valores de la sección eficaz del rigidizador del borde se han calculado con SHAPE-THIN. La rigidez del borde se muestra en la figura 04.

4 Rigidez eficaz del borde

A_s = 122,58 mm ²
I_s = 7.130 mm ⁴
z_s = 13,88 mm

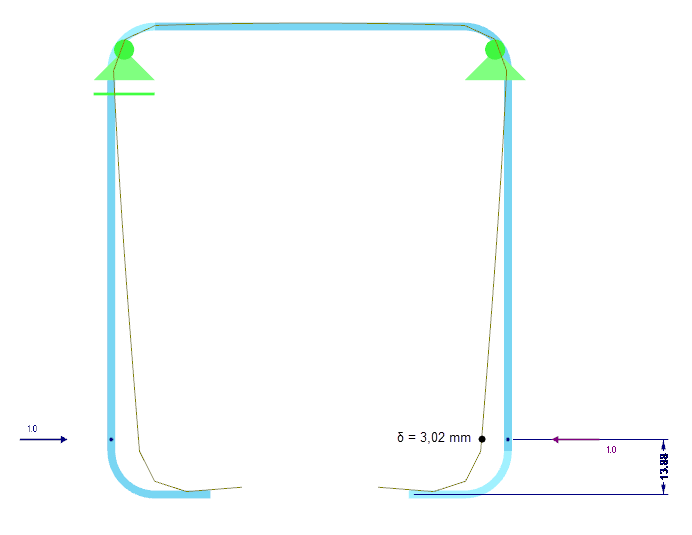
La rigidez elástica K de la rigidez del borde se determina en base al análisis estructural para la sección entera. Con este propósito, se aplica una carga de distancia unitaria u, que actúa en el centro de gravedad del rigidizador eficaz, en la sección y se calcula la deformación correspondiente δ del rigidizador. Para una sección rectangular w/h = t/t = 2/2 mm, la deformación da como resultado δ = 3,02 mm (figura 05).

5 Determinación de la rigidez elástica

La rigidez elástica por unidad de longitud K se puede calcular según [1], ec. 5.9 se puede calcular de la siguiente manera:

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

Rigidez elástica por unidad de longitud

La tensión crítica de la rigidez del borde resulta de [1], ec. 5.15 sobre:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

Tensión crítica crítica del rigidizador de borde

La relación de esbeltez se calcula según [1], ec. 5.12d para:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relación de esbeltez relativa

Según [1], 5.5.3.1 (7), el coeficiente de reducción para la inestabilidad de forma se calcula de la siguiente manera:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

coeficiente de reducción para la inestabilidad de la forma

El área de la sección eficaz reducida de la rigidez del borde se obtiene teniendo en cuenta el pandeo por flexión según [1], ec. 5.17 para:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

Área de la sección eficaz del rigidizador de borde

Propiedades de la sección eficaz bajo compresión pura

La sección se puede optimizar por medio de un cálculo iterativo. Para dos iteraciones, se obtienen los siguientes valores de la sección eficaz:

Área A_eff = 4,62 cm²
Distancia del centro de gravedad desde el alma z_s,eff = 42,18 mm
Desplazamiento del centro de gravedad e_N,y = z_s – * z_s,eff = 8,78 mm

Determinación de la sección eficaz bajo tensión de flexión pura

Alma

El alma se somete a tensión y por lo tanto es totalmente eficaz.

Ala con rigidizador de borde

Ala

Según [2], tabla 4.1, el valor de pandeo da como resultado:

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

Valor de pandeo del cordón

Según [2], 4.4 (2), la esbeltez de pandeo da como resultado:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

Esbeltez de pandeo del ala

La relación de esbeltez es menor que el valor límite 0,856 según [2], 4,4(2). Por lo tanto, no se requiere reducción.

Según [2], tabla 4.1, las anchuras eficaces dan como resultado:

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

Anchuras eficaces del cordón

rigidizador de borde

Según [1], 5.5.3.2 (5), el valor de pandeo da como resultado:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

valor de pandeo del rigidizador de borde

Según [2], 4.4 (2), la esbeltez de pandeo da como resultado:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Esbeltez de pandeo del rigidizador de borde

La relación de esbeltez es menor que el valor límite 0,748 según [1], 4,4(2). Por lo tanto, no es necesaria ninguna reducción, es decir: ρ = 1,0.

La primera aproximación de la anchura eficaz resulta de [1], ec. 5.13a para:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Primera aproximación de la anchura eficaz

Los valores de la sección eficaz del rigidizador del borde se han calculado con SHAPE-THIN. La rigidez del borde se muestra en la figura 06.

6 Wirksamer Steifenquerschnitt

A_s = 97,92 mm²
I_s = 6.271 mm⁴
z_s = 8,59 mm

7 Ermittlung der Federsteifigkeit

La rigidez elástica por unidad de longitud K se puede calcular según [1], ec. 5.9 se puede calcular de la siguiente manera:

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

Rigidez elástica por unidad de longitud

La tensión crítica de la rigidez del borde resulta de [1], ec. 5.15 sobre:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

Tensión crítica crítica del rigidizador de borde

La relación de esbeltez se calcula según [1], ec. 5.12d para:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relación de esbeltez relativa

Según [1], 5.5.3.1 (7), el coeficiente de reducción para la inestabilidad de forma se calcula de la siguiente manera:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

coeficiente de reducción para la inestabilidad de la forma

El área de la sección eficaz reducida de la rigidez del borde se obtiene teniendo en cuenta el pandeo por flexión según [1], ec. 5.17 para:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

Área de la sección eficaz del rigidizador de borde

Propiedades de la sección eficaz bajo tensión de flexión pura

Todas las partes de la sección son totalmente eficaces, de forma que la iteración ya no es necesaria.

Área A_eff = 6,86 cm²
Módulo de sección W_eff,y = 17,01 cm³

Cálculo de la sección de cargas combinadas debida a la compresión y flexión

La resistencia a compresión pura se calcula según [1], 6.1.3 (1) de la siguiente manera:

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

Resistencia a compresión pura

La resistencia a flexión pura se calcula según [1], 6.1.4.1 (1) de la siguiente manera:

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

Resistencia a flexión pura

El momento adicional resultante del desplazamiento del centro de gravedad se determina según [1], 6.1.9(2) de la siguiente manera:

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

Momento adicional del desplazamiento del centro de gravedad

El cálculo para la carga combinada de compresión y flexión según [1], 6.1.9 (1) da como resultado:

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

Comprobación de diseño para cargas combinadas de compresión y flexión

De esta manera, se realiza el cálculo.

Modelo de la sección en C conformada en frío en SHAPE-THIN

Las secciones conformadas en frío generales se pueden modelar en SHAPE-THIN. En los datos generales, active la casilla de verificación "partes c/t y las propiedades de la sección" (figura 08).

8 datos generales

Después, seleccione la opción "EN 1993-1-3 (sección conformada en frío)" en la pestaña "Partes c/t y sección eficaz" (figura 09) del cuadro de diálogo "Parámetros de cálculo".

La sección eficaz se debe determinar por separado para la compresión pura y la flexión pura. Por lo tanto, seleccione la casilla de verificación "Omitir momentos flectores adicionales debido al desplazamiento del centro de gravedad de la sección eficaz".

En el ejemplo, hemos calculado dos iteraciones de forma que estas dos iteraciones también están establecidas en SHAPE-THIN.

Las condiciones geométricas mencionadas en [2], 5.2 para la aplicabilidad de la norma se pueden comprobar opcionalmente. Para hacer esto, seleccione las casillas de verificación correspondientes.

9 Parámetros de cálculo

Primero se deben introducir los elementos de la sección. Las anchuras planas teóricas normalmente se generan de forma automática desde las condiciones geométricas, pero también se pueden crear según la definición del usuario en la tabla "1.7 Anchuras planas teóricas según EN 1993-1-3" (figura 10) o en el cuadro de diálogo correspondiente.

10 Tabla "1.8 Rigidizadores"

Los rigidizadores se pueden definir en la tabla "1.8 Rigidizadores" o en el cuadro de diálogo correspondiente (figura 11).

11 Tabla "1.9 Paneles"

Además, el panel de pandeo se debe especificar en la tabla "1.9 Paneles" (figura 12) o en el cuadro de diálogo correspondiente. Para hacer esto, seleccione los elementos del panel de pandeo. Los rigidizadores ubicados en el panel rigidizado se identifican automáticamente.

12 Tabla "2.1 Casos de carga"

Además, se crea un caso de carga para el esfuerzo de compresión y de flexión en la tabla "2.1 Casos de carga" (figura 13).

13 Tabla "3.1 Esfuerzos internos"

Después, introduzca los esfuerzos internos en la tabla "3.1 Esfuerzos internos" o en el cuadro de diálogo correspondiente (figura 14).

14 Propiedades de la sección eficaz

Los resultados de la sección eficaz están disponibles con el botón "Partes eficaces" (figura 15).

15 datos generales

Cálculo de secciones en C conformadas en frío en RF-STEEL Cold-Formed Sections

Las secciones conformadas en frío se pueden calcular según [1] y [2] con el módulo adicional RF-/STEEL Cold-Formed Sections.

En los datos generales, puede seleccionar primero la barra y caso de carga a calcular. Se selecciona "CEN" Como Anejo Nacional (figura 16).

16 Parameter des nationalen Anhangs

Puede ver y, si es necesario, ajustar los parámetros del Anejo Nacional en la pestaña "Conformación en frío (EN 1993-1-3)" de la ventana correspondiente (figura 17).

17 Detalles, pestaña "Conformación en frío"

En la configuración "Detalles", active la verificación de las secciones conformadas en frío en la pestaña "Conformación en frío" (figura 18).

18 Detalles, pestaña "Estabilidad"

Sólo se debe realizar el cálculo de la sección. Por lo tanto, se debe desactivar la casilla de verificación "Ejecutar análisis de estabilidad" en la pestaña "Estabilidad" de la configuración detallada (figura 19).

19 Figura 20 - Resultados

Después del cálculo, se muestran las siguientes salidas de la tabla, entre otras, las propiedades de la sección eficaz debido al esfuerzo axil N, momento flector M_y, momento flector M_z, esfuerzos internos y el cálculo completo (figura 20).

20 Tabla "1.7 Anchuras planas teóricas | EN 1993-1-3"

Base de datos de conocimientos

KB 001629 | Cálculo de una sección en C de pared delgada conformada en frío según EN 1993-1-3

Autor

Sra. von Bloh proporciona soporte técnico a nuestros clientes y es responsable del desarrollo del programa SHAPE-THIN, así como de las estructuras de acero y aluminio.

Enlaces

Referencias

Eurocódigo 3: Cálculo de estructuras de acero, partes 1‑3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Berlín: Beuth.
Eurocódigo 3: Diseño de estructuras de acero - Parte 1-5: Elementos estructurales enchapados. Editorial Beuth GmbH.
Kuhlmann, U. (2009). Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlín: Ernst y Sohn.

Descargas

Modelo de artículo técnico | Archivo de SHAPE-THIN 9

912 KB

Modelo del artículo técnico | Archivo de RFEM 5

504 KB

Modelo del artículo técnico | Archivo de RSTAB-8

404 KB

;