Voltar para a base de dados de conhecimento

13751x

001629

Sonja von Bloh, M.Sc.

2020-03-02

Dimensionamento de uma secção C de parede fina formada a frio de acordo com a norma EN 1993-1-3

O dimensionamento do estado limite último para secções formadas a frio de acordo com EN 1993-1-3 e EN 1993-1-5 pode ser realizado com a extensão de módulo RF-/STEEL Cold-Formed Sections. Além das secções formadas a frio a partir da base de dados de secções, também é possível dimensionar secções gerais a partir do SHAPE-THIN.

No exemplo seguinte do Steel Structures Yearbook 2009 {%>

Sistema

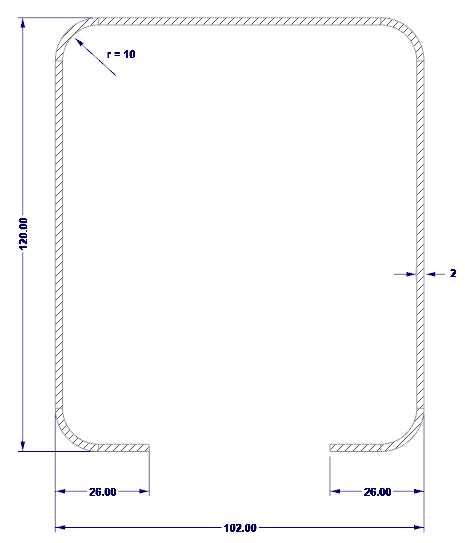
Sistema e carregamento são apresentados na Figura 01.

1 Sistema e carregamento (dimensões em mm, força em kN)

Material

S 355 EN 10025-2
E = 210 000 N/mm²
G = 80 769 N/mm²
ν = 0,3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1,00 (dimensionamento de acordo com o CEN)

Dimensões externas

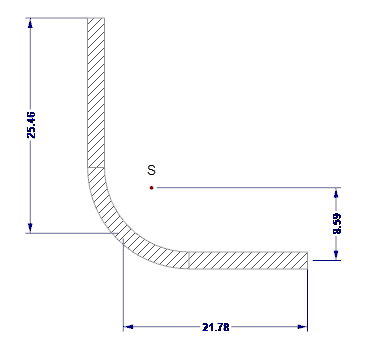
As dimensões externas da secção são apresentadas na Figura 02.

2 Außenabmessungen des Querschnitts in mm

H = 102 mm (altura da alma)
b = 120 mm (largura da corda)
c = 26 mm (comprimento dos rebordos)
t = 2 mm (espessura do núcleo de aço)

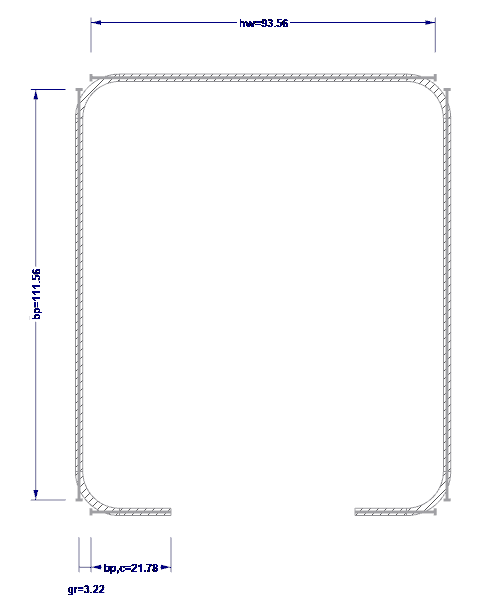
Valor nominal das larguras planas

Os valores nominaos da largura plana são determinados de acordo com {%>

3 Larguras planas nominais em mm

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

Valor nominal das larguras planas

Verificação das relações largura-espessura

As relações largura-espessura são verificadas de acordo com {%>

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

As relações largura-espessura são cumpridas.

Verificação das dimensões do reforço

As dimensões do reforço são verificadas de acordo com {%>0,2 ≤ c/b = 26/120 = 0,22 ≤ 0,6

Os rebordos podem ser aplicados como reforços.

Verificação do ângulo entre o reforço e o elemento plano

O ângulo entre o reforço e o elemento plano é de 90° dentro dos limites de 45° e 135° mencionados em {%>

Determinação da secção efetiva

Para secções de aço que não estão sujeitas a simetria dupla e estão sujeitas a compressão, a posição do centro geométrico da secção efetiva muda em comparação com a secção bruta. A força de compressão externa que atua centralmente na secção bruta atua agora excentricamente na secção efetiva e é criado um momento de flexão adicional. De acordo com {%>

Determinação da secção efetiva sujeita a compressão pura

De acordo com {%>

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

Fator ε

Alma

De acordo com {%>

k_{σ} = 4

coeficiente de encurvadura local

De acordo com {%>

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Esbelteza de encurvadura da alma

A relação de esbelteza é superior ao valor limite 0,673 de acordo com {%>

De acordo com {%>

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

Fator de redução para a alma

De acordo com {%>

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

Altura efetiva da alma

Banzo com reforço de borda

No primeiro passo, é determinada uma primeira abordagem para a secção efetiva do reforço com a assunção de que a rigidez da borda atua como um apoio rígido e que σ_{com, Ed} = f_yb/γ_M0 .

corda

De acordo com {%>

k_{σ} = 4

coeficiente de encurvadura local

De acordo com {%>

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Esbelteza de encurvadura do banzo

A relação de esbelteza é superior ao valor limite 0,673 de acordo com {%>

De acordo com {%>

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

Fator de redução para o banzo

De acordo com {%>

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

Largura efetiva do banzo

reforço de borda

De acordo com {%>

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

valor de encurvadura do reforço de borda

De acordo com {%>

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Esbelteza de encurvadura do reforço de borda

A relação de esbelteza é inferior ao valor limite 0,748 de acordo com [1], 4.4 (2). Assim, não é necessária redução, ou seja: ρ = 1,0.

A primeira abordagem da largura efetiva resulta de {%>

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Primeira abordagem da largura efetiva

No segundo passo, o fator de redução para a forma de instabilidade da secção é determinado utilizando a primeira abordagem eficaz para a secção, tendo em conta a mola de translação elástica.

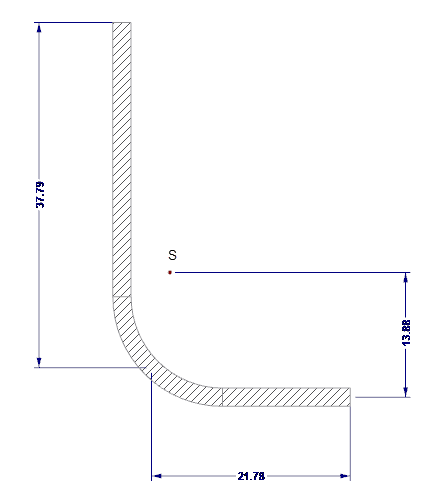
Os valores da secção efetiva da rigidez de borda são calculados com o SHAPE-THIN. A rigidez da borda é apresentada na Figura 04.

4 Rigidez efetiva da borda

A_s = 122,58 mm²
I_s = 7130 mm⁴
z_s = 13,88 mm

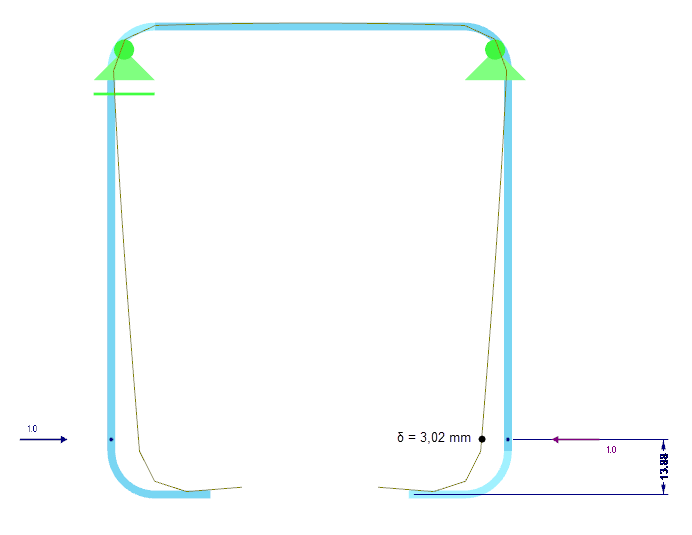
A rigidez da mola K da rigidez da borda é determinada com base numa análise estrutural para toda a secção. Para este efeito, é aplicada uma carga de distância unitária u, atuando no centro geométrico do reforço efetivo, à secção e a correspondente deformação δ do reforço é calculada. Para uma secção retangular w/h = t/t = 2/2 mm, a deformação resulta em δ = 3,02 mm (Figura 05).

5 Determinação da rigidez da mola

A rigidez da mola por unidade de comprimento K pode ser calculada de acordo com {%>

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

Rigidez da mola por unidade de comprimento

A tensão crítica da rigidez da borda resulta de {%>

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

Tensão crítica do reforço de borda

A relação de esbelteza é calculada de acordo com {%>

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relação de esbelteza relativa

De acordo com {%>

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

coeficiente de redução para a instabilidade da forma

A área da secção efetiva reduzida da rigidez da borda é obtida tendo em consideração a encurvadura por flexão de acordo com {%>

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

Área de secção efetiva do reforço de borda

Propriedades da secção efetiva sujeita a compressão pura

A secção pode ser otimizada através de um cálculo iterativo. Para duas iterações, resulta nos seguintes valores de secção efetiva:

Área A_ef = 4,62 cm²
Distância do centro geométrico da alma z_s,ef = 42,18 mm
Deslocamento do centro geométrico e_N,y = z_s - * z_s,ef = 8,78 mm

Determinação da secção efetiva sob tensão por flexão pura

Alma

A alma está sujeita a tração e, portanto, é totalmente eficaz.

Banzo com reforço de borda

No primeiro passo, é determinada uma primeira abordagem para a secção efetiva do reforço com a assunção de que a rigidez da borda atua como um apoio rígido e que σ_{com, Ed} = f_yb/γ_M0 .

corda

De acordo com {%>

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

Valor de encurvadura da corda

De acordo com {%>

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

Esbelteza de encurvadura do banzo

A relação de esbelteza é inferior ao valor limite 0,856 de acordo com {%>

De acordo com {%>

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

Larguras efetivas da corda

reforço de borda

De acordo com {%>

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

valor de encurvadura do reforço de borda

De acordo com {%>

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Esbelteza de encurvadura do reforço de borda

A relação de esbelteza é inferior ao valor limite 0,748 de acordo com [1], 4.4 (2). Assim, não é necessária redução, ou seja: ρ = 1,0.

A primeira abordagem da largura efetiva resulta de {%>

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Primeira abordagem da largura efetiva

Os valores da secção efetiva da rigidez de borda são calculados com o SHAPE-THIN. A rigidez da borda é apresentada na Figura 06.

6 Wirksamer Steifenquerschnitt

A_s = 97,92 mm²
I_s = 6271 mm⁴
z_s = 8,59 mm

7 Ermittlung der Federsteifigkeit

A rigidez da mola por unidade de comprimento K pode ser calculada de acordo com {%>

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

Rigidez da mola por unidade de comprimento

A tensão crítica da rigidez da borda resulta de {%>

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

Tensão crítica do reforço de borda

A relação de esbelteza é calculada de acordo com {%>

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relação de esbelteza relativa

De acordo com {%>

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

coeficiente de redução para a instabilidade da forma

A área da secção efetiva reduzida da rigidez da borda é obtida tendo em consideração a encurvadura por flexão de acordo com {%>

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

Área de secção efetiva do reforço de borda

Propriedades da secção efetiva sob tensão de flexão pura

Todas as partes da secção são totalmente eficazes, pelo que a iteração não é necessária.

Área A_ef = 6,86 cm²
Módulo de secção W_ef,y = 17,01 cm³

Dimensionamento da secção da carga combinada devido à compressão e flexão

A resistência à compressão pura é calculada de acordo com {%>

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

Resistência à compressão pura

A resistência à flexão pura é calculada de acordo com {%>

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

Resistência à flexão pura

O momento adicional resultante do desvio do centróide é determinado de acordo com {%>

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

Momento adicional a partir do deslocamento do centro de gravidade

O dimensionamento para carregamento combinado a partir de compressão e flexão de acordo com {%>

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

Verificação para carregamento combinado a partir de compressão e flexão

O verificação é assim cumprida.

Modelação de uma secção em C formada a frio no SHAPE-THIN

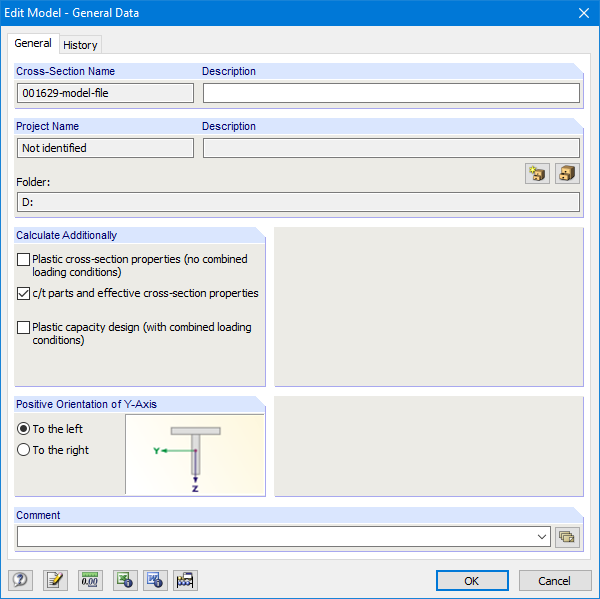
As seções gerais formadas a frio podem ser modeladas no SHAPE-THIN. Nos dados gerais, ative a caixa de seleção "Partes c/t e propriedades da seção efetiva" (Figura 08).

8 Dados gerais

De seguida, selecione a opção "EN 1993-1-3 (secção formada a frio)" no separador "partes c/t e secção efetiva" (Figura 09) da caixa de diálogo Parâmetros de cálculo.

A secção efetiva tem de ser determinada separadamente para compressão pura e flexão pura. Portanto, selecione a caixa de seleção "Negligenciar momentos de flexão adicionais devido ao deslocamento do centro de gravidade da secção efetiva".

No exemplo, calculamos com duas iterações para que também sejam definidas duas iterações no SHAPE-THIN.

As condições geométricas mencionadas em {%>

9 Parâmetros de cálculo

Os elementos da secção tem de ser introduzidos em primeiro lugar. Os valores nominaos das larguras planas são geralmente geradas automaticamente a partir das condições de geometria, mas também pode ser criado pelo utilizador definido na Tabela "1.7 Larguras planas nominais de acordo com EN 1993-1-3" (Figura 10) ou na correspondente caixa de diálogo.

10 Tabela 1.8 Reforços

Os reforços podem depois ser definidos na Tabela "1.8 Reforços" ou na correspondente caixa de diálogo (Figura 11).

11 Tabela 1.9 Painéis

Além do mais, o painel de encurvadura tem de ser especificado na Tabela "1.9 Painéis" (Figura 12) ou na correspondente caixa de diálogo. Para isso, selecione os elementos do painel de encurvadura. Os reforços localizados no painel de encurvadura são identificados automaticamente.

12 Tabela 2.1 Casos de carga

Além disso, é criado um caso de carga para a força de compressão e flexão na Tabela "2.1 Casos de carga" (Figura 13).

13 Tabela 3.1 Esforços internos

De seguida, introduza as forças internas na Tabela "3.1 Forças internas" ou na correspondente caixa de diálogo (Figura 14).

14 Propriedades da secções efetivas

Os resultados da secção efetiva estão disponíveis com o botão "Partes efetivas" (Figura 15).

15 Dados gerais

Verificação do dimensionamento de uma secção C formada a frio em secções formadas a frio RF-/STEEL

As secções formadas a frio podem ser dimensionadas de acordo com {%>

Nos dados gerais, tem de selecionar primeiro a barra e o caso de carga a ser dimensionado. "CEN" é selecionado como anexo nacional (Figura 16).

16 Parameter des nationalen Anhangs

Pode ver e, se necessário, ajustar os parâmetros do Anexo nacional no separador "Formadas a frio (EN 1993-1-3)" da janela correspondente (Figura 17).

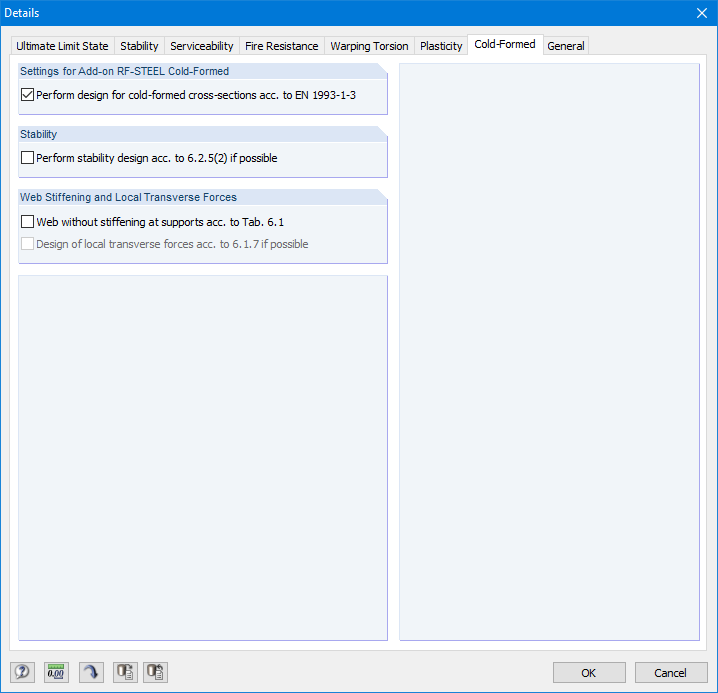
17 Detalhes, separador Secções formadas a frio

Nas configurações de detalhe, ative a verificação do dimensionamento para secções formadas a frio no separador "Formada a frio" (Figura 18).

18 Detalhes, separador Estabilidade

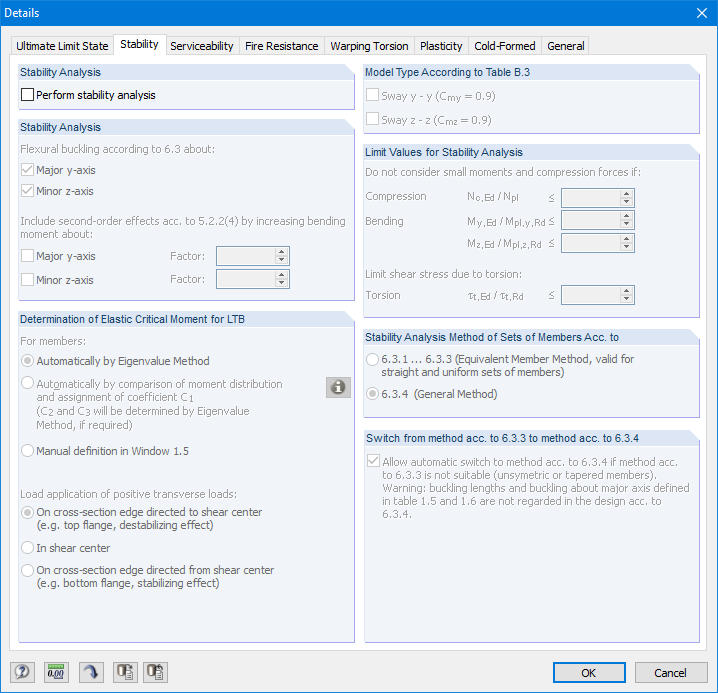
Apenas deve ser realizado o dimensionamento da secção. Portanto, a caixa de seleção "Realizar análise de estabilidade" no separador "Estabilidade" das configurações detalhadas deve ser desativada (Figura 19).

19 Figura 20 - Resultados

Após o cálculo, são apresentadas as tabelas de saída correspondentes, entre outras coisas, as propriedades da secção efetiva devido à força axial N, momento de flexão M_y, momento de flexão M_z, forças internas e todo o dimensionamento (Figura 20).

20 Tabela 1.7 Larguras planas nominais segundo a EN 1993-1-3

Base de dados de conhecimento

KB 001629 | dimensionamento de uma secção C de parede fina formada a frio de acordo com a norma EN 1993-1-3

Autor

A Eng.ª von Bloh fornece apoio técnico a clientes e também é responsável pelo desenvolvimento do programa RSECTION e pelas estruturas de aço e alumínio.

Ligações

Referências

Comité Europeia para a normalização. (2010). Eurocódigo 3: Bemessung und Konstruktion von Stahlbauten – Teil 1-3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Beuth Verlag GmbH, Berlin, 2010
EC 3. (2009). Eurocódigo 3: Dimensionamento de estruturas de aço – Parte 1-5: Elementos estruturais constituídos por placas. Beuth GmbH.
Kuhlmann, U. Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlin: Ernst & Sohn, 2009

Downloads

Modelo de artigo técnico | Ficheiro do SHAPE-THIN 9

912 KB

Modelo do artigo técnico | Ficheiro do RFEM 5

504 KB

Modelo de artigo técnico | Ficheiro do RSTAB-8

404 KB

;