13637x

001629

Sonja von Bloh, M.Sc.

2020-03-02

Wymiarowanie przekroju ceowego cienkościennego zgodnie z EN 1993-1-3

Obliczenia stanu granicznego nośności przekrojów formowanych na zimno zgodnie z EN 1993-1-3 i EN 1993-1-5 można przeprowadzić za pomocą rozszerzenia RF-/STEEL Cold-Formed Sections. Oprócz profili formowanych na zimno z bazy danych przekrojów, SHAPE-THIN umożliwia także obliczanie przekrojów uogólnionych.

W poniższym przykładzie z Steel Structures Yearbook 2009 [3], obliczenia przekroju dla belki jednoprzęsłowej o cienkościennym, formowanym na zimno przekroju ceowym są przeprowadzane zgodnie z obciążenie siłą normalną. Belka poddana jest działaniu siły osiowej. Ceownik jest modelowany w SHAPE-THIN, a następnie wymiarowany w RF-/STEEL Cold-Formed Sections.

System

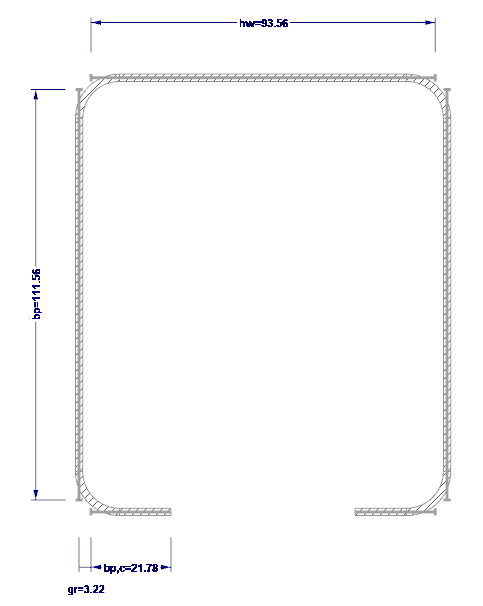
Układ i obciążenie są pokazane na rysunku 01.

1 Układ i obciążenie (wymiary w mm, siła w kN)

Materiał

S 355 EN 10025-2
E = 210 000 N/mm²
G = 80 769 N/mm²
ν = 0,3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1,00 (wymiarowanie zgodne z CEN)

Wymiary zewnętrzne

Zewnętrzne wymiary przekroju pokazano na rysunku 02.

2 Außenabmessungen des Querschnitts in mm

H = 102 mm (wysokość środnika)
b = 120 mm (szerokość pasa)
c = 26 mm (długość zagięcia krawędzi)
t = 2 mm (grubość rdzenia stalowego)

Umowne szerokości części płaskich przekroju

Umowne szerokości części płaskich są określane zgodnie z [1], 5.1. oraz przedstawione na rysunku 03.

3 Nominalne szerokości części płaskich w mm

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

Umowne szerokości części płaskich przekroju

Sprawdzanie proporcji szerokości do grubości

Stosunki szerokości do grubości są sprawdzane zgodnie z [1], 5.2(1).

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

Proporcje szerokości do grubości są spełnione.

Kontrola wymiarów elementów usztywniających

Wymiary usztywnienia są sprawdzane zgodnie z [1], 5.2(2).
0,2 ≤ c/b = 26/120 = 0,22 ≤ 0,6

Zagięcia krawędzi mogą pełnić rolę elementów usztywniających.

Sprawdzenie kąta pomiędzy elementem usztywniającym a przyległą ścianką przekroju

Kąt pomiędzy elementem usztywniającym i płaskim wynosi 90° i mieści się w granicach 45° do 135°, o których mowa w [1], 5.5.3.2(1).

Określenie przekroju efektywnego

W przypadku ściskanych przekrojów stalowych, które nie są bisymetryczne, środek ciężkości efektywnego przekroju ulega przesunięciu w stosunku do przekroju brutto. Zewnętrzna siła ściskająca, oddziałująca centralnie na przekrój brutto, działa teraz mimośrodowo na przekrój efektywny, co powoduje powstanie dodatkowego momentu zginającego. Zgodnie z [1] należy uwzględnić dodatkowe momenty wynikające z przesunięcia środka ciężkości. W związku z powyższym oprócz przekroju efektywnego dla czystych naprężeń ściskających, należy określić przekrój efektywny dla czystych naprężeń przy zginaniu.

Określenie efektywnego przekroju przy czystym ściskaniu

Zgodnie z [2], 4.4 (2) współczynnik ten wynosi:

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

Współczynnik ε

środnik

Zgodnie z [2], tabela 4.1, wartość współczynnika niestateczności miejscowej wynosi:

k_{σ} = 4

współczynnik wyboczenia płyty

Zgodnie z [2], 4.4 (2) smukłość wyboczeniowa wynosi:

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Smukłość przy wyboczeniu środnika

Współczynnik smukłości jest większy niż wartość graniczna 0,673 zgodnie z [2], 4.4(2). Z tego względu wymagana jest redukcja.

Zgodnie z [2], 4.4 (2) współczynnik redukcyjny wynosi:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

Współczynnik redukcyjny dla środnika

Zgodnie z [2], Tabela 4.1, efektywna wysokość środnika wynika z [2], Tabela 4.1:

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

Efektywna wysokość środnika

Pas z usztywnieniem krawędzi

W pierwszym podejściu efektywny przekrój elementu usztywniającego wyznaczany jest przy założeniu, że element ten stanowi sztywną podporę dla krawędzi przekroju oraz, że σ_{com, Ed} = f_yb/γ_M0 .

pas

Zgodnie z [2], tabela 4.1, wartość współczynnika niestateczności miejscowej wynosi:

k_{σ} = 4

współczynnik wyboczenia płyty

Zgodnie z [2], 4.4 (2) smukłość wyboczeniowa wynosi:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Smukłość wyboczeniowa pasa

Współczynnik smukłości jest większy niż wartość graniczna 0,673 zgodnie z [2], 4.4(2). Z tego względu wymagana jest redukcja.

Zgodnie z [2], 4.4 (2) współczynnik redukcyjny wynosi:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

Współczynnik redukcyjny dla pasa

Zgodnie z [2], tabela 4.1, efektywna szerokość półki wynosi:

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

Szerokość efektywna półki

usztywnienie brzegowe

Zgodnie z [1], 5.5.3.2 (5), wartość współczynnika niestateczności miejscowej wynosi:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

wartość wyboczenia usztywnienia krawędzi

Zgodnie z [2], 4.4 (2) smukłość wyboczeniowa wynosi:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Smukłość wyboczeniowa usztywnienia krawędzi

Współczynnik smukłości jest mniejszy niż wartość graniczna 0,748 zgodnie z [1], 4.4(2). Nie ma więc konieczności redukcji, to znaczy: ρ = 1,0.

Pierwsze podejście szerokości efektywnej wynika z [1], równ. 5.13a do:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Pierwsze podejście szerokości efektywnej

W kolejnym kroku określany jest współczynnik redukcyjny z uwagi na niestateczności postaciowe z wykorzystaniem efektywnego przekroju wyznaczonego w pierwszym podejściu. Na tym etapie uwzględnia się sprężyste podparcie translacyjne.

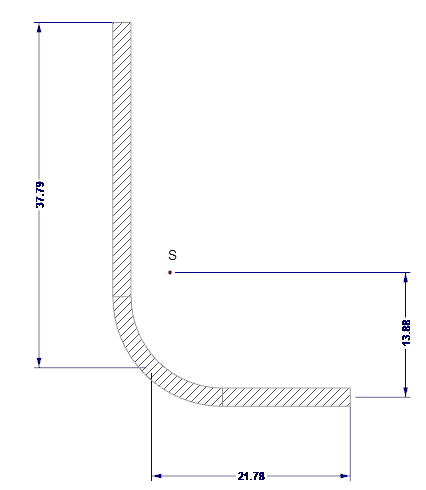
Własności efektywne przekroju elementu usztywniającego krawędź są obliczane za pomocą SHAPE-THIN. Sztywność krawędzi pokazano na rysunku 04.

4 Efektywna sztywność krawędzi

A_s = 122,58 mm ²
I_s = 7.130 mm ⁴
z_s = 13,88 mm

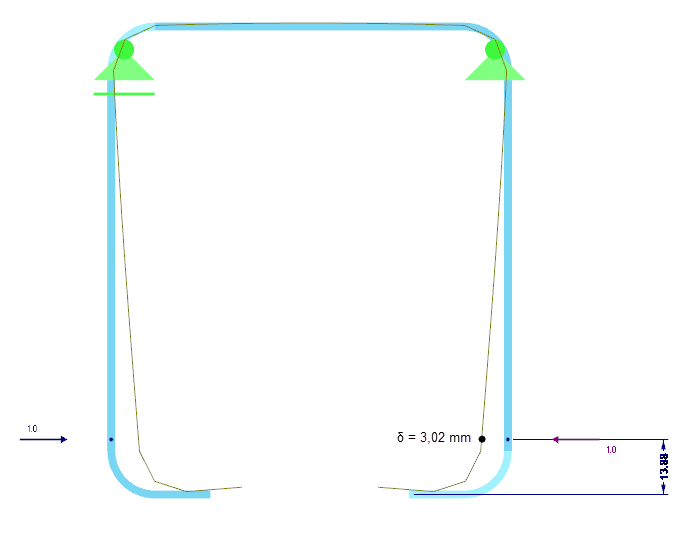
Sztywność sprężysta K elementu usztywniającego krawędź jest określana na podstawie analizy statyczno-wytrzymałościowej dla całego przekroju. W tym celu do przekroju przykłada się jednostkowe obciążenie działające w środku ciężkości efektywnego elementu usztywniającego i obliczane jest odpowiadające temu odkształcenie δ. W przypadku przekroju prostokątnego w/h = t/t = 2/2 mm odkształcenie wynosi δ = 3,02 mm (Rysunek 05).

5 Określanie sztywności sprężyny translacyjnej

Sztywność sprężystą na jednostkę długości K można obliczyć według [1], równ. 5.9 można obliczyć w następujący sposób:

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

Sztywność sprężysta na jednostkę długości

Naprężenie krytyczne sztywności krawędzi wynika z [1], równ. 5.15 w dniu:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

Naprężenie krytyczne usztywnienia krawędzi

Współczynnik smukłości obliczany jest według [1], równ. 5.12d do:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Smukłość względna

Zgodnie z [1], 5.5.3.1 (7), współczynnik redukcji z uwagi na niestateczność kształtu jest obliczany w następujący sposób:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

współczynnik redukcji niestateczności kształtu

Zredukowane efektywne pole przekroju sztywności krawędzi uzyskuje się poprzez uwzględnienie wyboczenia giętnego zgodnie z [1], równ. 5.17 do:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

Efektywne pole przekroju usztywnienia krawędzi

Efektywne właściwości przekroju przy czystym ściskaniu

Przekrój efektywny można zoptymalizować powtarzając procedurę iteracyjnie. W przypadku dwóch iteracji uzyskuje się następujące efektywne własności przekroju:

Pole przekroju A_eff = 4,62 cm²
Odległość środka ciężkości od środnika z_{s, eff} = 42,18 mm
Przemieszczenie środka ciężkości e_{N, y} = z_s – * z_{s, eff} = 8,78 mm

Określenie przekroju efektywnego dla naprężeń od czystego zginania

środnik

Środnik jest poddawany rozciąganiu, a zatem jest w pełni efektywny.

Pas z usztywnieniem krawędzi

pas

Zgodnie z [2], tabela 4.1, wartość współczynnika niestateczności miejscowej wynosi:

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

Wartość wyboczenia pasa

Zgodnie z [2], 4.4 (2) smukłość wyboczeniowa wynosi:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

Smukłość wyboczeniowa pasa

Współczynnik smukłości jest mniejszy niż wartość graniczna 0,856 zgodnie z [2], 4.4(2). Dzięki temu nie ma konieczności redukcji.

Zgodnie z [2], tabela 4.1, szerokości efektywne wynoszą:

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

Szerokości efektywne pasa

usztywnienie brzegowe

Zgodnie z [1], 5.5.3.2 (5), wartość współczynnika niestateczności miejscowej wynosi:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

wartość wyboczenia usztywnienia krawędzi

Zgodnie z [2], 4.4 (2) smukłość wyboczeniowa wynosi:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Smukłość wyboczeniowa usztywnienia krawędzi

Współczynnik smukłości jest mniejszy niż wartość graniczna 0,748 zgodnie z [1], 4.4(2). Nie ma więc konieczności redukcji, to znaczy: ρ = 1,0.

Pierwsze podejście szerokości efektywnej wynika z [1], równ. 5.13a do:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Pierwsze podejście szerokości efektywnej

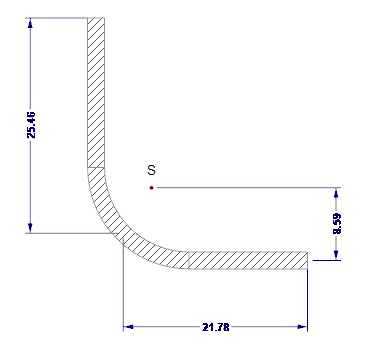
Własności efektywne przekroju elementu usztywniającego krawędź są obliczane za pomocą SHAPE-THIN. Sztywność krawędzi pokazano na rysunku 06.

6 Wirksamer Steifenquerschnitt

A_s = 97,92 mm ²
I_s = 6 271 mm ⁴
z_s = 8,59 mm

7 Ermittlung der Federsteifigkeit

Sztywność sprężystą na jednostkę długości K można obliczyć według [1], równ. 5.9 można obliczyć w następujący sposób:

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

Sztywność sprężysta na jednostkę długości

Naprężenie krytyczne sztywności krawędzi wynika z [1], równ. 5.15 w dniu:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

Naprężenie krytyczne usztywnienia krawędzi

Współczynnik smukłości obliczany jest według [1], równ. 5.12d do:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Smukłość względna

Zgodnie z [1], 5.5.3.1 (7), współczynnik redukcji z uwagi na niestateczność kształtu jest obliczany w następujący sposób:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

współczynnik redukcji niestateczności kształtu

Zredukowane efektywne pole przekroju sztywności krawędzi uzyskuje się poprzez uwzględnienie wyboczenia giętnego zgodnie z [1], równ. 5.17 do:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

Efektywne pole przekroju usztywnienia krawędzi

Efektywne właściwości przekroju przy czystym naprężeniu zginającym

Wszystkie części przekroju są w pełni efektywne, dzięki czemu iteracja nie jest konieczna.

Obszar A_eff = 6,86 cm²
Moduł przekroju W_{eff, y} = 17.01 cm³

Wymiarowanie przekroju w złożonym stanie obciążenia: ściskanie i zginanie

Nośność na czyste ściskanie jest obliczana zgodnie z [1], 6.1.3 (1) w następujący sposób:

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

Nośność na czyste ściskanie

Nośność na czyste zginanie jest obliczana zgodnie z [1], 6.1.4.1 (1) w następujący sposób:

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

Czysta nośność na zginanie

Dodatkowy moment wynikający z przesunięcia środka ciężkości jest określany zgodnie z [1], 6.1.9(2) w następujący sposób:

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

Dodatkowy moment z przesunięcia środka ciężkości

Obliczenia dla obciążeń złożonych od ściskania i zginania zgodnie z [1], 6.1.9 (1):

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

Warunek projektowy dla złożonego obciążenia od ściskania i zginania

Warunek nośności jest zatem spełniony.

Modelowanie ceownika w SHAPE-THIN

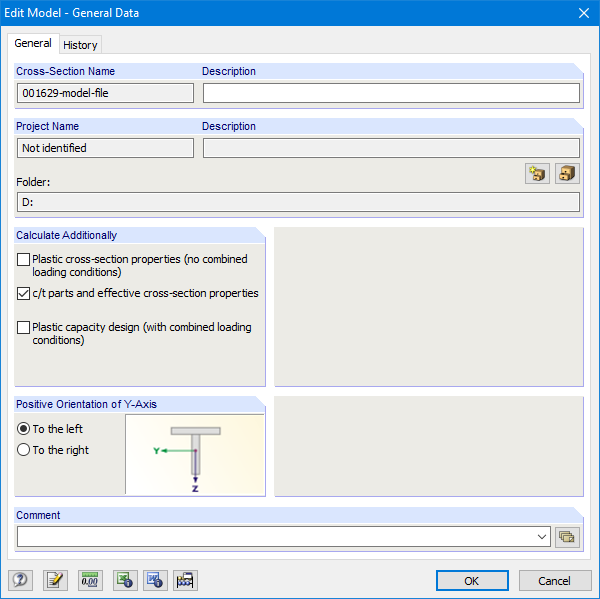
Uogólnione przekroje formowane na zimno można modelować w SHAPE-THIN. W danych ogólnych należy zaznaczyć opcję „Części c/t i efektywne właściwości przekroju” (Rysunek 08).

8 Ogólne dane

Następnie w zakładce „Części c/t i przekrój efektywny” (Rysunek 09) w oknie dialogowym Parametry obliczeń należy wybrać opcję „EN 1993-1-3 (Przekrój formowany na zimno)”.

Przekrój efektywny należy określać osobno dla czystego ściskania i czystego zginania. Z tego względu należy zaznaczyć opcję „Zignorować dodatkowe momenty zginające ze względu na przesunięcie środka ciężkości przekroju efektywnego”.

W przykładzie tym, obliczenia przeprowadzono przy użyciu dwóch iteracji, dlatego też w SHAPE-THIN ustawione są dwie iteracje.

Opcjonalnie można sprawdzić warunki geometryczne, o których mowa w [2], 5.2., czy mają one zastosowanie do normy. W tym celu należy zaznaczyć odpowiednie pola wyboru.

9 Parametry obliczeń

Najpierw należy wprowadzić elementy przekroju. Umowne szerokości części płaskich są zazwyczaj generowane automatycznie na podstawie zdefiniowanej geometrii, ale można je również zadać w tabeli „1.7 Nominalne szerokości płaskie zgodnie z EN 1993-1-3” (Rysunek 10) lub w odpowiednim oknie dialogowym.

10 Tabela 1.8 Elementy usztywniające

Elementy usztywniające można zdefiniować w tabeli "1.8 Usztywnienia" lub w odpowiednim oknie dialogowym (Rysunek 11).

11 Tabela 1.9 Panele

Dodatkowo należy zaznaczyć panel do określenia wyboczenia w tabeli "1.9 Panele" (Rysunek 12) lub w odpowiednim oknie dialogowym. W tym celu należy wybrać elementy panelu wyboczeniowego. Elementy usztywniające znajdujące się w usztywnionym panelu są rozpoznawane automatycznie.

12 Tabela 2.1 Przypadki obciążeń

Dodatkowo w tabeli "2.1 Przypadki obciążeń" (Rysunek 13) tworzony jest przypadek obciążenia dla siły ściskającej i zginania.

13 Tabela 3.1 Siły wewnętrzne

Następnie należy wprowadzić siły wewnętrzne w tabeli "3.1 Siły wewnętrzne" lub w odpowiednim oknie dialogowym (Rysunek 14).

14 Charakterystyki przekroju efektywnego

Wyniki dla przekroju efektywnego są dostępne po naciśnięciu przycisku "Części efektywne" (Rysunek 15).

15 Ogólne dane

Wymiarowanie ceowników formowanych na zimno w RF/STEEL Cold-Formed Sections

Profile zimnogięte można wymiarować zgodnie z [1] i [2] za pomocą modułu dodatkowego RF-/STEEL Cold-Formed Sections.

W Danych ogólnych należy najpierw wybrać pręt i przypadek obciążenia, które mają zostać obliczone. Jako załącznik krajowy wybrano „CEN” (rysunek 16).

16 Parameter des nationalen Anhangs

Parametry załącznika krajowego można wyświetlić, a w razie potrzeby dostosować, w zakładce "Formowane na zimno (EN 1993-1-3)" w odpowiednim oknie (Rysunek 17).

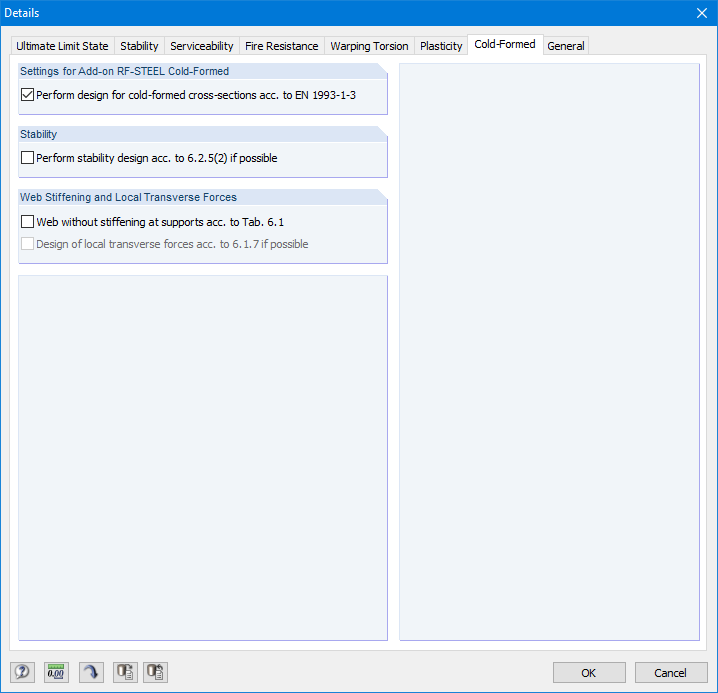
17 Szczegóły, zakładka Przekroje formowane na zimno

W Ustawieniach szczegółowych należy aktywować kontrolę obliczeń przekrojów formowanych na zimno w zakładce "Formowane na zimno" (Rysunek 18).

18 Szczegóły, zakładka Stateczność

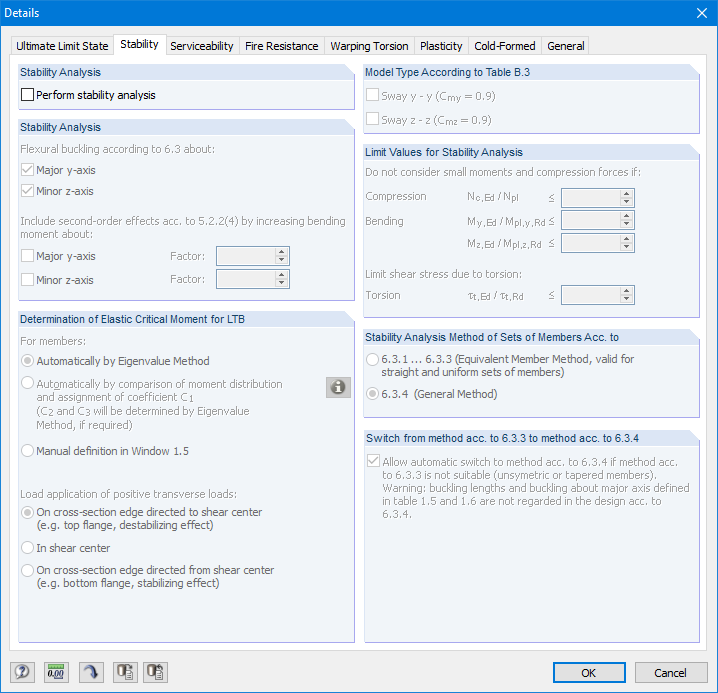
Należy przeprowadzać tylko obliczenia dla wymiarowania przekroju. Z tego względu należy dezaktywować pole wyboru „Przeprowadzić analizę stateczności” w zakładce „Stateczność“ w ustawieniach szczegółowych (Rysunek 19).

19 Rysunek 20 - Wyniki

Po zakończeniu obliczeń odpowiednie tabele wyników przedstawiają, między innymi, efektywne właściwości przekroju wywołane siłą osiową N, momentem zginającym M_y, momentem zginającym M_z, siłami wewnętrznymi oraz podsumowanie obliczeń (Rysunek 20).

20 Tabela 1.7 Nominalne szerokości części płaskich | EN 1993-1-3

Baza informacji

KB 001629 | Wymiarowanie przekroju ceowego cienkościennego zgodnie z EN 1993-1-3

Autor

Pani von Bloh zapewnia naszym klientom wsparcie techniczne i jest odpowiedzialna za rozwój programu SHAPE‑THIN oraz konstrukcji stalowych i aluminiowych.

Odnośniki

Odniesienia

Eurokod 3: Projektowanie konstrukcji stalowych - Część 1-3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Berlin: Beuth.
Eurokod 3: Projektowanie konstrukcji stalowych - Część 1-5: Platerowane elementy konstrukcyjne. Wydawnictwo Beuth GmbH.
Kuhlmann, U. (2009). Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlin: Ernst & Sohn.

Pobrane

Model do artykułu technicznego | Plik SHAPE-THIN 9

912 KB

Model do artykułu technicznego | Plik RFEM 5

504 KB

Model do artykułu technicznego | Plik RSTAB-8

404 KB

;