返回知识库

4126x

001606

Dipl.-Ing. （FH）Robert Fogl

2019-11-04

在RFEM中平滑地面内力

在计算面模型时，内力对每个有限元单元都是单独计算的。由于逐个单元的结果通常不连续分布，因此 RFEM 会考虑相邻单元的影响对内力进行平滑处理。随着内力的不连续分布通过这种方法进行调整。结果评估可以更加清晰和简单。

您可以在程序中选择不同的选项来显示未平滑或平滑的结果。在RFEM 用户手册中有详细的介绍。

RFEM 5 在线手册

在这篇技术文章中也介绍了用于分析面内力的平滑选项。

知识库 001571 | 内力图/面应力 - 平滑选项

下面通过一个示例来说明有限元单元中的内力值的确定方法。除了有限元的位置外，板块理论 - Mindlin 或 Kirchhoff - 在这个过程中也起作用。

示例：按照 Mindlin 和 Kirchhoff 板

1 示例

创建尺寸为 4 m ⋅ 3 m 的二维模型板。板件在短边界线上铰接。较大边界线的旋转受到约束。为避免横向应变效应，材料泊松比应设置为零。为了根据 Kirchhoff 和 Mindlin 的板弯曲理论对内力的确定进行比较，选择 80 cm 厚的板。两种弯矩理论的分界线比值 d/L = 0.2（见 FAQ 003158）。

常见问题和解答 (FAQ) | 计算使用面单元是否足够,还是使用实体单元更好?

这里有限元网格的网格尺寸设置为1 m。因此，有 4 ⋅ 3 个有限元单元。

板件上作用荷载 p = 5 kN/m²。自重不适用于该荷载工况。

未平滑的内力

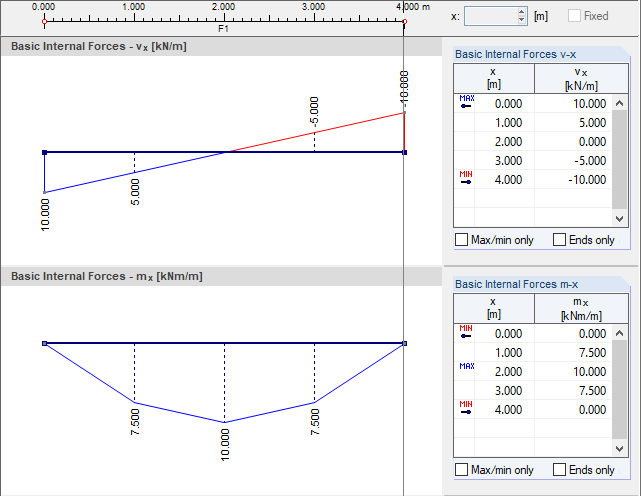
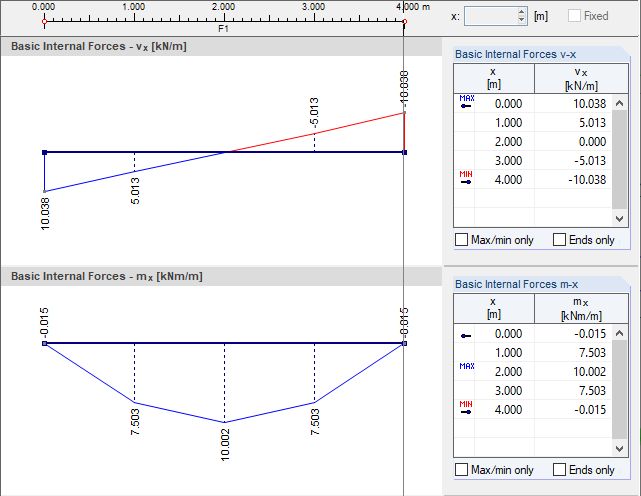
内力 v_x和 m_x的计算内核的结果是针对在板中心的纵向截面进行考虑。通过选择“不连续”可以查看各个单元单元的未平滑内力。根据 Mindlin 和 Kirchhoff 弯曲理论，可以得到如图 02 中所示的图形。

2 结果未平滑，据Mindlin（左）和Kirchhoff（右）

内部节点标准平滑

对于位于面上的有限元节点，首先由相邻有限元单元的节点值得出其算术平均值。对于这种方法，单元必须位于一个面上，并且在同一侧。该节点不能是面中用户自定义的节点。

对于 x = 1.00 m 处的不连续位置，这些值在输出中为下表（这一步的结果不适用于输出）。

明德林：

$v_{x} (1) = \frac{7.5 \cdot 2.5}{2} = 5$
$m_{x} (1) = \frac{8.772 \cdot 5.351}{2} = 7.061$

根据 Mindlin，内部节点标准平滑
基尔霍夫：

$v_{x} (1) = \frac{7.785 \cdot 2.595}{2} = 5.19$
$m_{x} (1) = \frac{7.954 \cdot 7.904}{2} = 7.929$

标准内部节点平滑（根据基尔霍夫）

端节点平滑

在面（“面内连续”平滑选项）或模型（“连续总计”）的边缘处没有可用于平均节点值的相邻有限元单元。因此，需要使用另一种分两步执行的方法。

第一步是计算那些不在面或模型边缘的节点的平均值。计算边缘节点数值时，有限元单元中心为原始值。第二步，计算边缘节点的平均值。

以下值是针对边缘节点在 x = 0.00 m 时的值。

明德林：

$v_{x} (0) = 7.5 \cdot (7.5 - 5) = 10$
$m_{x} (0.5) = \frac{5.351 \cdot 2.982}{2} = 4.167$
$m_{x} (0) = 4.167 \cdot (4.167 - 7.061) = 1.272$

按照 Mindlin 平滑边缘节点
基尔霍夫：

$v_{x} (0) = 7.785 \cdot (7.785 - 5.19) = 10.381$
$m_{x} (0.5) = \frac{7.954 \cdot 0.379}{2} = 4.167$
$m_{x} (0) = 4.167 \cdot (4.167 - 7.929) = 0.404$

根据基尔霍夫平滑边缘节点

剪力

根据 Mindlin 理论，剪力的计算采用挠度的一阶导数。

v_{x} = \frac{5 \cdot G \cdot h}{6} \cdot (\frac{\partial w}{\partial x} Φ_{y})

v_{y} = \frac{5 \cdot G \cdot h}{6} \cdot (\frac{\partial w}{\partial y} Φ_{x})

Mindlin 剪力计算

该值由计算内核确定并直接使用。根据面中有限元节点的位置，如上所述对剪力进行平滑。

在基尔霍夫弯曲理论中，剪力采用挠度的三阶导数。

v_{x} = - \frac{E \cdot h^{3}}{12 \cdot (1 - μ^{2})} \cdot (\frac{\partial^{3} w}{\partial x^{3}} \frac{\partial^{3} w}{\partial x \partial y^{2}})

v_{y} = - \frac{E \cdot h^{3}}{12 \cdot (1 - μ^{2})} \cdot (\frac{\partial^{3} w}{\partial y^{3}} \frac{\partial^{3} w}{\partial x^{2} \partial y})

剪力按照 Kirchhoff

这种使用三阶导数的数值确定导致相当大的精度损失。因此，不使用计算内核的剪力，而是通过改进的方法由弯矩的推导得出。

v_{x} = \frac{\partial m_{x}}{\partial x} \frac{\partial m_{xy}}{\partial y}

v_{y} = \frac{\partial m_{y}}{\partial y} \frac{\partial m_{xy}}{\partial x}

弯矩的推导

公式中的弯矩 m_x 、m_y和 m_xy表示根据上述方法确定的平滑值。与使用计算内核计算得出的剪力值更精确。

v_{x} {(0)}^{} = v_{x} {(1)}^{-} = 7.929 - 0.404 = 7.525

v_{x} {(1)}^{} = v_{x} {(2)}^{-} = 10.429 - 7.929 = 2.5

v_{x} (1) = \frac{7.525 2.5}{2} = 5.013

v_{x} (0) = 7.525 7.525 - 5.013 = 10.038

剪力数值

弯矩

虽然积分点处的弯矩值与理论值相对应，但是当使用双曲抛物面函数进行平滑时，外推法会导致精度下降。双曲抛物面只是在单元中近似弯矩分布。出于这个原因，使用了一种改进的算法，用先进的剪力积分法代替外推法。由于面单元中的剪力分布被假定为双曲抛物面（二阶曲面），因此该面的积分表示为三阶曲面，它可以更准确地显示弯矩分布。

该方法相当于上述通过弯矩的导数确定剪力的公式。该弯矩的计算公式如下：

m_{x} = \int (v_{x} - \frac{\partial m_{xy}}{\partial y}) dx m_{x, 0}

m_{y} = \int (v_{y} - \frac{\partial m_{xy}}{\partial x}) dy m_{y, 0}

弯矩的推导

积分常数 m_x,0和 m_y,0是根据杆件中心的值计算的。

m_{x, C} = \frac{\int_{S} m_{x} dS}{S}

m_{y, C} = \frac{\int_{S} m_{y} dS}{S}

[THESIS.THESISTITLE]

单元的面

杆件中心-数值条件

内力的数值按照上述方法计算；的积分，通过数值积分。然后对由此得出的弯矩按照用于内部节点或者边缘节点的方法进行平滑。

在 Mindlin 的弯矩理论中，得出该示例中的值为以下数值。

第一个单元:

$v_{x} (x) = 10 - 5 x$
$m_{x} (x) = \int v_{x} dx m_{x, 0} = 10 x - \frac{5}{2} x^{2} m_{x, 0}$
$m_{x, C} = m_{x} (0.5) = 4.167 = \int_{0}^{1} 10 x - \frac{5}{2} x^{2} m_{x, 0} = {[\frac{10}{2} x^{2} - \frac{5}{6} x^{3} m_{x, 0} x]}_{0}^{1} = 4.167 m_{x, 0}$
$m_{x, 0} = m_{x} (0) = 4.167 - 4.167 = 0$
$m_{x} {(1)}^{-} = 10 - \frac{5}{2} 0 = 7.5$

根据 Mindlin 的弯曲理论
第二个元素：

$v_{x} (x) = 5 - 5 x$
$m_{x} (x) = \int v_{x} dx + m_{x, 0} = 5 x - \frac{5}{2} x^{2} + m_{x, 0}$
$m_{x, C} = m_{x} (1.5) = 9.167 = \int_{0}^{1} 5 x - \frac{5}{2} x^{2} + m_{x, 0} = {[\frac{5}{2} x^{2} - \frac{5}{6} x^{3} + m_{x, 0} x]}_{0}^{1} = 1.667 + m_{x, 0}$
$m_{x, 0} = m_{x} (1)^{+} = 9.167 - 1.667 = 7.5$
$m_{x} (1) = \frac{m_{x} (1)^{-} + m_{x} (1)^{+}}{2} = \frac{7.5 + 7.5}{2} = 7.5$

第二单元使用 Mindlin 的弯曲理论

3 按照Mindlin平滑内力vx和mx分布

以下是基于基尔霍夫弯曲理论的值。

第一个单元:

$v_{x} (x) = 10.038 - 5.025 x$
$m_{x} (x) = \int v_{x} dx m_{x, 0} = 10.038 x - \frac{5.025}{2} x^{2} m_{x, 0}$
$m_{x, C} = m_{x} (0.5) = 4.167 = \int_{0}^{1} 10.038 x - \frac{5.025}{2} x^{2} m_{x, 0} = {[\frac{10.038}{2} x^{2} - \frac{5.025}{6} x^{3} m_{x, 0} x]}_{0}^{1} = 4.182 m_{x, 0}$
$m_{x, 0} = m_{x} (0) = 4.167 - 4.182 = - 0.015 m_{x} {(1)}^{-} = 10.038 - \frac{5.025}{2} - 0.015 = 7.511$

第一个单元 Kirchhoff 弯曲理论
第二个元素：

$v_{x} (x) = 5.013 - 5.013 x$
$m_{x} (x) = \int v_{x} dx + m_{x, 0} = 5.013 x - \frac{5.013}{2} x^{2} + m_{x, 0}$
$m_{x, C} = m_{x} (1.5) = 9.167 = \int_{0}^{1} 5.013 x - \frac{5.013}{2} x^{2} + m_{x, 0} = {[\frac{5.013}{2} x^{2} - \frac{5.013}{6} x^{3} + m_{x, 0} x]}_{0}^{1} = 1.671 + m_{x, 0}$
$m_{x, 0} = m_{x} (1)^{+} = 9.167 - 1.671 = 7.496$
$m_{x} (1) = \frac{m_{x} (1)^{-} + m_{x} (1)^{+}}{2} = \frac{7.511 + 7.496}{2} = 7.503$

第二单元使用Kirchhoff弯曲理论