Сглаживание внутренних сил поверхности в программе RFEM

Программа содержит различные параметры для отображения сглаженных или не сглаженных результатов. Подробнее данные параметры описываются в Руководстве пользователя RFEM.

• Онлайн-руководство RFEM 5

Некоторые варианты сглаживания для расчета поверхностных внутренних сил и напряжений описаны также в данной технической статье.

• КБ 001571 | Диаграмма внутренних сил/Напряжения на поверхности - опции сглаживания

В настоящей статье приводится пример, показывающий использование сглаживания внутренних сил в конечных элементах для более простого определения значений. Кроме расположения конечного элемента, в данном процессе важную роль также играет выбор теории пластин - Миндлина или Кирхгофа.

Пример: Пластина по Миндлину и Кирхгофу

1 Пример:

Сначала создадим двумерную модель пластины размером 4 м ⋅ 3 м. Пластина должна быть с обеих сторон шарнирно закреплена по более коротким граничным линиям. Более длинные граничные лини защемлены против кручения. Чтобы ограничить действие поперечной деформации, установим для материала нулевой коэффициент Пуассона. Для сравнения внутренних сил, определенных с помощью теории изгиба пластин по Кирхгофу либо по Миндлину, зададим толщину пластины 80 см. Таким образом, в предельной области между двумя теориями изгиба получается отношение d/L = 0,2 (см. FAQ 003158).

• faq | Достаточно ли выполнить расчет с элементами поверхности или лучше использовать элементы тел?

Для простоты шаг сетки КЭ задан равным 1 м. Таким образом мы получим 4 ⋅ 3 конечных элемента.

На пластину действует нагрузка p = 5 кН/м². Собственный вес в нагружении не учитывается.

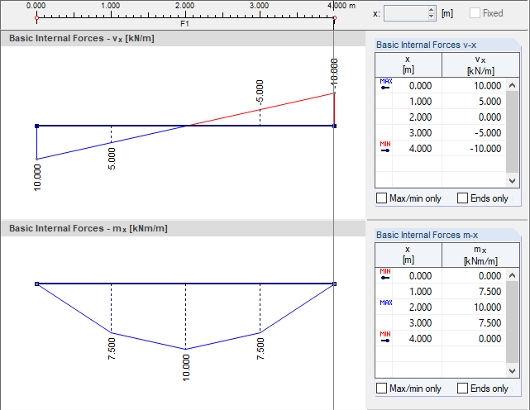
Не сглаженные внутренние силы

Результаты, полученные решателем для внутренних сил, v_x и m_x относятся к продольному сечению, проходящему через центр пластины. Распределение не сглаженных внутренних сил по элементам можно отобразить с помощью функции «Не непрерывно». Распределение по теориям пластин Миндлина и Кирхгофа показано на рисунке 02.

2 Несглаженные результаты по Миндлину (слева) и Кирхгофу (справа)

Стандартное сглаживание для внутренних узлов

Для узлов сетки КЭ, лежащих внутри поверхности, сначала определяется среднее арифметическое из узловых значений смежных конечных элементов. В данном подходе элементы должны лежать на поверхности и на одной и той же стороне потенциальной внутренней линии. Узел не должен быть узлом поверхности, заданным пользователем.

При положении разрыва в точке x = 1,00 м данные внутренние значения являются следующими (результат данного шага недоступен для вывода).

• Миндлин:

  $${\mathrm{v}}_{\mathrm{x}}\left(1\right) = \frac{7.5 · 2.5}{2} = 5$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{8.772 · 5.351}{2} = 7.061$$

  Стандартное сглаживание для внутренних узлов по Миндлину
• Кирхгоф:

  $${\mathrm{v}}_{\mathrm{x}}\left(1\right) = \frac{7.785 · 2.595}{2} = 5.19$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{7.954 · 7.904}{2} = 7.929$$

  Стандартное сглаживание для внутренних узлов по Кирхгофу

Сглаживание для краевых узлов

На краях поверхности (функция сглаживания «Непрерывно внутри поверхности») или модели («Непрерывно в целом») нет смежных конечных элементов, которые можно было бы применить для усреднения узловых значений. Поэтому используется другой метод, который выполняется в два этапа.

На первом этапе рассчитываются средние значения тех узлов, которые не расположены на краях поверхности или модели. Значения узлов, расположенных на краях, рассчитываются таким образом, чтобы исходные значения оставались в центре конечных элементов. На втором этапе определяются усредненные значения краевых узлов.

Значения краевых узлов в x = 0,00 м являются следующими.

• Миндлин:

  $${\mathrm{v}}_{\mathrm{x}}\left(0\right) = 7.5 · (7.5 - 5) = 10$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}(0.5) = \frac{5.351 · 2.982}{2} = 4.167$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 · (4.167 - 7.061) = 1.272$$

  Сглаживание краевых узлов по Миндлину
• Кирхгоф:

  $${\mathrm{v}}_{\mathrm{x}}\left(0\right) = 7.785 · (7.785 - 5.19) = 10.381$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}(0.5) = \frac{7.954 · 0.379}{2} = 4.167$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 · (4.167 - 7.929) = 0.404$$

  Сглаживание краевых узлов по Кирхгофу

Поперечные силы

По Миндлину сдвигающие силы рассчитываются через первую производную прогиба.

Эти значения определяются решателем и используются напрямую. Затем выполняется сглаживание сдвигающих сил, как описано выше, в зависимости от положения узла сетки конечных элементов внутри поверхности.

В теории изгиба пластин по Кирхгофу сдвигающие силы рассчитываются через третью производную прогиба.

Такое определение значения с помощью третьей производной приводит к значительной потере точности. По этой причине сдвигающие силы, рассчитанные решателем, не используются, а определяются по улучшенному методу с помощью дифференцирования моментов.

Моменты m_x, m_y и m_xy в уравнениях представляют собой сглаженные значения, которые определяются по методам, описанным выше. В результате получены более точные значения сдвигающих сил, чем из расчета с помощью решателя.

Моменты

Несмотря на то, что значения моментов в точках интегрирования соответствуют теоретическим значениям, экстраполяция при сглаживании с применением функции гиперболического параболоида приводит к потере точности. Гиперболический параболоид только приблизительно отражает распределение моментов в элементе. По этой причине используется улучшенный алгоритм, который заменяет экстраполяцию расширенным методом интеграции сил сдвига. Поскольку предполагается, что распределение сил сдвига в поверхностном элементе имеет форму гиперболического параболоида (поверхность второго порядка), интеграл данной поверхности представляет собой поверхность третьего порядка, которая с большей точностью отображает распределение моментов.

Данный подход соответствует указанным выше уравнениям для вычисления сдвигающих сил через производные моментов. Затем моменты определяются с помощью следующих уравнений.

Константы интегрирования m_x,0 и m_y,0 рассчитываются по условиям значения в центре стержня.

Значения внутренних сил определяются описанными выше методами, а интегралы рассчитываются численным интегрированием. Определенные данным образом моменты затем сглаживаются по методу внутренних узлов или краевых узлов.

По теории изгиба пластин Миндлина в нашем примере мы получим следующие значения.

• Первый элемент:

  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 10 - 5 \mathrm{x}$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} {\mathrm{m}}_{\mathrm{x},0} = 10 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(0.5) = 4.167 = {\int }_0^{1}10 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{10}{2} {\mathrm{x}}^2 - \frac{5}{6} {\mathrm{x}}^3 {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 4.167 {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 - 4.167 = 0$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}{\left(1\right)}^{-} = 10 - \frac{5}{2} 0 = 7.5$$

  Первый элемент с помощью теории изгиба по Миндлину
• Второй элемент:

  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 5 - 5 \mathrm{x}$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} + {\mathrm{m}}_{\mathrm{x},0} = 5 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(1.5) = 9.167 = {\int }_0^{1}5 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{5}{2} {\mathrm{x}}^2 - \frac{5}{6} {\mathrm{x}}^3 + {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 1.667 + {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}(1{)}^{+} = 9.167 - 1.667 = 7.5$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{{\mathrm{m}}_{\mathrm{x}}(1{)}^{-} + {\mathrm{m}}_{\mathrm{x}}(1{)}^{+}}{2} = \frac{7.5 + 7.5}{2} = 7.5$$

  Второй элемент на основе теории изгиба по Миндлину

3 Сглаженное распределение внутренних сил v-x и m-x по Миндлину

По теории изгиба пластин Кирхгофа мы получим следующие значения.

• Первый элемент:

  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 10.038 - 5.025 \mathrm{x}$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} {\mathrm{m}}_{\mathrm{x},0} = 10.038 \mathrm{x} - \frac{5.025}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(0.5) = 4.167 = {\int }_0^{1}10.038 \mathrm{x} - \frac{5.025}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{10.038}{2} {\mathrm{x}}^2 - \frac{5.025}{6} {\mathrm{x}}^3 {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 4.182 {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 - 4.182 = - 0.015 {\mathrm{m}}_{\mathrm{x}}{\left(1\right)}^{-} = 10.038 - \frac{5.025}{2} - 0.015 = 7.511$$

  Первый элемент с помощью теории изгиба по Кирхгофу
• Второй элемент:

  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 5.013 - 5.013 \mathrm{x}$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} + {\mathrm{m}}_{\mathrm{x},0} = 5.013 \mathrm{x} - \frac{5.013}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(1.5) = 9.167 = {\int }_0^{1}5.013 \mathrm{x} - \frac{5.013}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{5.013}{2} {\mathrm{x}}^2 - \frac{5.013}{6} {\mathrm{x}}^3 + {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 1.671 + {\mathrm{m}}_{\mathrm{x},0}$$

  
  

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}(1{)}^{+} = 9.167 - 1.671 = 7.496$$

  
  

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{{\mathrm{m}}_{\mathrm{x}}(1{)}^{-} + {\mathrm{m}}_{\mathrm{x}}(1{)}^{+}}{2} = \frac{7.511 + 7.496}{2} = 7.503$$

  Второй элемент с помощью теории изгиба по Кирхгофу

4 Сглаженное распределение внутренних сил v-x и m-x по Кирхгофу

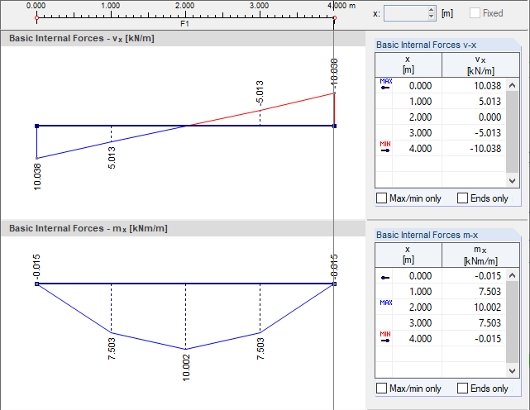
В процессе сглаживания в программе последовательно выполняются описанные выше шаги. Сглаженные значения можно отобразить графически с помощью функции отображения «Непрерывно внутри поверхности».

База знаний

KB 001606 | Сглаживание внутренних сил поверхности в программе RFEM