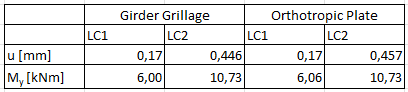
例如, [2]通常建议定义一个梁式栅格。 该格栅结构很好地体现了组合梁混凝土板的双轴结构行为。 但是,在这种情况下建模工作量较大,并且栅格在局部离散点上不准确。 下面将梁栅格的建模与正交各向异性板的建模进行比较。
首先,我们使用一个简单的结构来定义梁的格栅结构。然后定义正交各向异性板。 最后,解释了结果和差异。
系统
- 截面钢筋: HE-A 200
- 钢材: S235
- 截面混凝土: d = 100 mm
- 材料混凝土: C30/37
- 荷载: 5 kN/m²
- 横向应变: nu = 0.2
在 SHAPE-MASSIVE 中创建组合截面,并按照定义的截面到混凝土板的偏心导入到 RFEM 中。 假设截面的有效宽度为60 cm。 截面的重心在混凝土和钢筋之间的连接处向上移动了 0.8 cm。 因此在计算时需要考虑连接节点。 向下移动了 5 cm。
选择支座方案本身时,不会因为约束变形而产生约束。
两个体系的荷载作用相同。
- LC1 = 5 kN/m²
- LC2 = 10 kN(x 方向 = 跨中,y 方向 = 外侧边缘)
梁式格栅结构
梁式栅格格栅的要求(来自[1] ):
- 恒定施工高度
- 直线梁桥
- 简单对称截面
- 两根主梁都支撑在每个支撑轴上,该轴垂直于桥的纵轴。
- 支座轴上几乎刚性的横向加劲
- 支座坐标轴无约束翘曲
- 用于桁架分析的结构软件必须能够计算杆件单元。
抗弯刚度的计算值(来自 [2]):
抗扭刚度计算值:
截面性质:
- IT = 0 cm 4
- Iy = (100cmx (10cm)³)/12 = 8333.3 cm 4
- A = 1000 cm²
- Ay = 833 cm²
在程序中使用有效的截面属性进行输入。 此处考虑了杆件的剪切刚度。 计算混凝土板的横向刚度(宽度 = 1 m)。
正交各向异性板结构
在正交各向异性板结构中,主梁的建模方法与梁栅格相同。 然后将这些梁集成到混凝土翼缘中。 刚度传递全部由主梁传递,横向由混凝土翼缘传递。 有限元网格大小的定义与次梁的距离相同,均为50 cm。
正交各向异性板的刚度矩阵是对称的,并且只应用于主对角线。 板的纵向抗弯刚度和抗扭刚度与梁格栅的横向钢筋相同,几乎为零。
抗弯刚度计算值:
抗扭刚度计算值:
在程序中,使用用户自定义的刚度输入数据。
小结