Tak jako například v [2] se často setkáme s doporučením použít nosníkový rošt, kterým lze také dobře modelovat dvouosé chování nosné betonové desky spřaženého nosníku. Modelování je ovšem náročnější a nepřesné v lokálních diskrétních bodech. Níže porovnáme modelování nosníkového roštu a ortotropní desky.
Nejdříve uvedeme parametry konstrukce. Poté pomocí jednoduchého systému popíšeme nosníkový rošt a následně zadáme ortotropní desku. Nakonec porovnáme výsledky a všimneme si případných odchylek.
Systém
- Průřez Ocel: HE-A 200
- Materiál Ocel: S235
- Průřez Beton: d = 100 mm
- Materiál Beton: C30/37
- Zatížení: 5 kN/m²
- Příčné protažení: nu = 0,2
Spřažený průřez se vytvoří v programu SHAPE-THIN a načte se v programu RFEM se zadanou excentricitou průřezu k betonové desce. Spolupůsobící šířka se přitom nastaví obecně na 60 cm. Těžiště průřezu se posune vzhledem ke spáře mezi betonem a ocelí o 0,8 cm směrem nahoru. V případě podpor se tak bude počítat se spárou. Podpory se proto posunou o 5 cm směrem dolů.
Rozmístění podpor bylo navrženo tak, aby nedocházelo k žádnému vynucenému přetvoření vlivem omezení deformace.
U obou systémů se bude uvažovat stejné zatížení.
- ZS1 = 5 kN/m²
- ZS2 = 10 kN (směr x = střed pole, směr y = vnější okraj)
Konstrukce nosníkového roštu
Předpoklady u nosníkového roštu (z [1]):
- konstantní výška konstrukce
- rovný trámový most
- jednoduše symetrický průřez
- hlavní nosníky jsou podepřeny v každé ose podpory, přičemž osa podpory je kolmá na podélnou osu mostu
- téměř tuhé příčné vyztužení v osách podpor
- neomezená deplanace v osách podpor
- použitý program pro výpočty prutových konstrukcí musí umět počítat prutové prvky poddajné ve smyku
Výpočtová hodnota tuhosti v ohybu (z [2]):
Výpočtová hodnota tuhosti v kroucení:
Průřezové charakteristiky:
- IT = 0 cm4
- Iy =(100cmx(10cm)³)/12= 8333,3 cm4
- A = 1 000 cm²
- Ay = 833 cm²
Jako vstupní údaje se v programu zadají účinné průřezové hodnoty. Zohledňuje se přitom tuhost prutů ve smyku. Tuhost se stanoví pro betonovou desku v příčném směru (šířka = 1 m).
Ortotropní desková konstrukce
V ortotropním deskovém systému se hlavní nosníky modelují stejně jako u nosníkového roštu. Tyto nosníky se dále integrují do betonové desky. Tuhost v podélném směru zcela přebírají hlavní nosníky a v příčném směru betonová deska. Velikost sítě konečných prvků přitom odpovídá vzdálenosti mezi příčnými nosníky, která činí 50 cm.
Matice tuhosti ortotropní desky je symetrická a je obsazena pouze na hlavních diagonálách. Hodnoty tuhosti pro ohyb v podélném směru desky a kroucení byly nastaveny stejně jako u příčných prutů nosníkového roštu téměř na nulu.
Výpočtová hodnota tuhosti v ohybu:
Výpočtová hodnota tuhosti v kroucení:
Jako vstupní údaje se v programu zadají uživatelem stanovené hodnoty tuhosti.
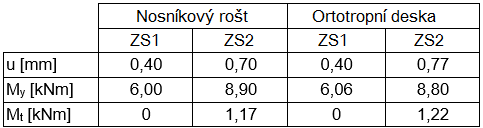
Závěr