在 RFEM 中使用肋杆件类型表示的优点
需要考虑下立梁的刚度或柔性。 由此可以看出它对内力分布和变形的影响。
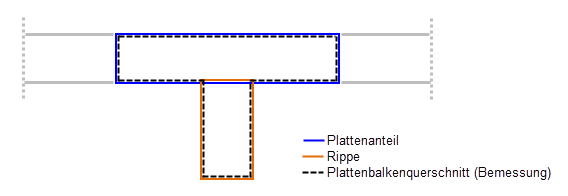
肋参数
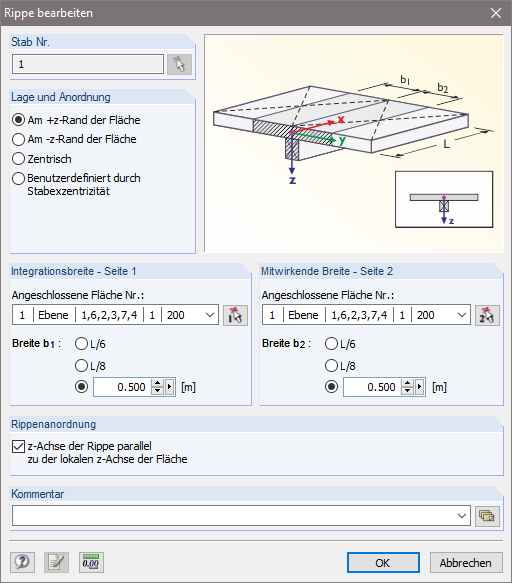
对于三维位置的肋,有两个基本参数。 首先是积分宽度,它定义了内力积分的面积。 为此 ,每侧的积分面积不得超过多个面。 其次,必须定义肋的排列方式。 位置数据参照面(包括肋)的局部坐标系。
肋截面
作为肋的截面部分,需要在面附加定义这样的截面部分。 对于 T 形梁的设计,程序会生成 T 形梁的总截面。
内力计算
在进行设计之前,要确定内力以及与 T 形梁(通常是 T 形截面或 L 形截面)的重心的关系。 为此,集成了板的内力分量和肋部分的内力。 内力垂直于肋轴的方向进行积分。
对于板构件,以下内力来自于面中的内力积分。 假设肋部和面的局部坐标系相同。 如果内力不同,则必须事先将内力变换到肋的局部坐标系上。
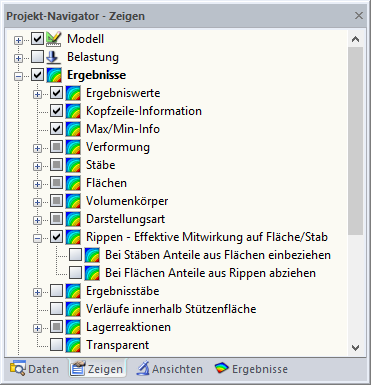
肋部分的内力与包括肋截面在内的杆件的内力相对应。 在 RFEM 中,可以在不显示内力计算的面分量的情况下显示内力。 您可以在项目导航器 - 显示中的“结果” - “肋 - 面/杆件上的有效贡献”中进行调整。
得出的 T 形梁内力总和是由板和肋部分的内力参照 T 形梁截面的重心得出的。
对于 T 形截面,可以得到生成的 T 形梁的弯矩,例如,如下所示:
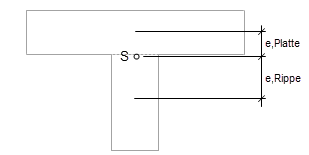
My = My,板+ My,rib - e板∙ N板+ e肋∙ N肋
程序始终按照默认设置确定 T 形梁截面的等效内力。
二维肋
对于 T 形梁,这基本上不是一个纯二维问题。 用户需要注意的是,在二维环境中考虑肋部必然会受到简化。 因为在二维环境中不可能对齐偏心单元,所以T型梁截面的重心轴在面的平面上。 这种方法在考虑结构的刚度时需要额外的步骤。
除了三维肋的参数外,为了考虑 T 形梁截面的刚度,还必须应用二维肋的其他参数。 通过在二维内部考虑肋部,叠加刚度得到集成宽度区域b1和b2。 根据肋参数的默认设置,在集成宽度区域内降低面刚度是激活的。 但是需要注意的是,该应用程序会导致肋沿轴的刚度集中,因此在现实中不会出现这种情况,也不会在 3D 模型中显示肋部。
因为在二维中不能显示偏心,所以要考虑偏心对刚度(即附加的施泰纳分量)的影响。 对于抗扭刚度,T 形梁截面和面的一部分被叠加。 T 形梁截面的抗扭刚度活动可以手动进行折减。 通常,不可能为有效的抗扭刚度指定折减系数或百分比值,因为这取决于截面的几何形状。
因此最好使用 3D 版本的 RFEM 代替 2D 版本的软件来表示下部横梁。

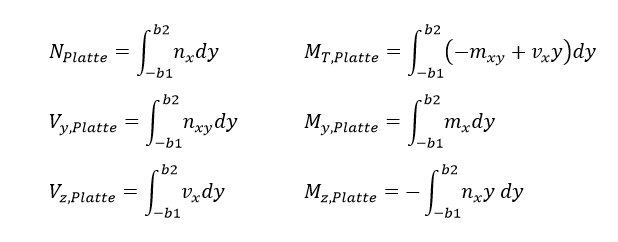


































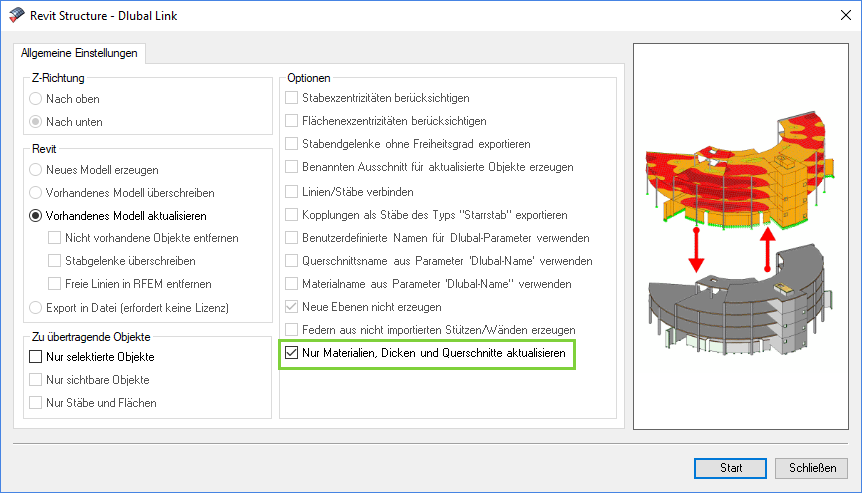








_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)