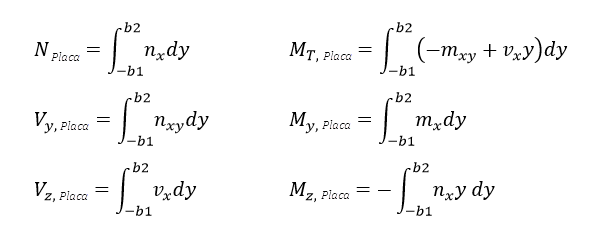Ventajas de la representación mediante el tipo de barra nervio en RFEM
Se considera la rigidez o flexibilidad de una viga de cuelgue. Por lo tanto, se puede representar su influencia en la distribución de esfuerzos internos y la deformación.
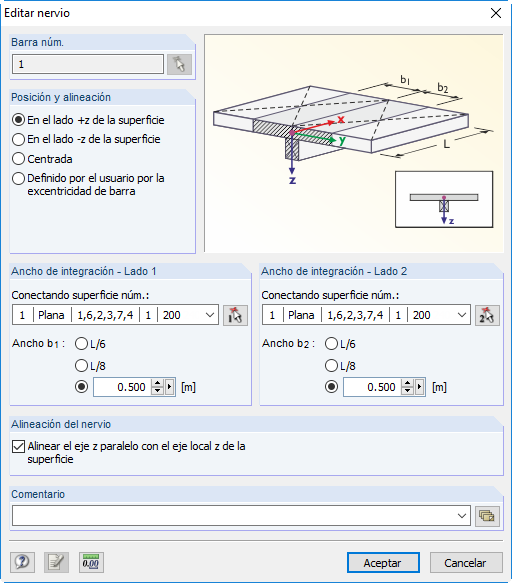
Parámetros de la nervadura
Hay dos parámetros principales para la nervadura en una posición tridimensional. Por un lado, el ancho de integración, que define el área de integración de los esfuerzos internos. Debe tenerse en cuenta que el área de integración en cada lado no puede extenderse sobre varias superficies. Por otro lado, es necesario especificar dónde se colocará el nervio. La información relativa a la posición se refiere al sistema de ejes local de la superficie a la que está conectado el nervio.
Sección transversal de la nervadura
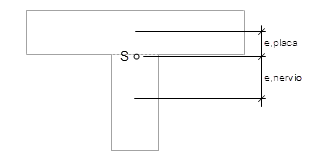
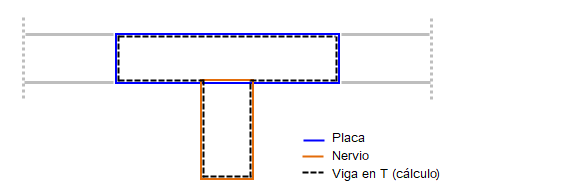
La sección transversal del nervio debe definirse como la parte de la sección transversal que está presente además de la superficie. Para el diseño, la sección transversal total de la viga en T se crea internamente.
Determinación de esfuerzos internos para el cálculo.
Antes del cálculo, los esfuerzos internos para la sección transversal de la viga en T, generalmente una sección transversal en T o en L, se determinan internamente por integración y referencia al centro de gravedad de la sección transversal de la viga en T. El componente de fuerzas internas de la losa y el componente del nervio están integrados. Los esfuerzos internos están integrados en ángulo recto con el eje del nervio.
Para la parte de losa, los siguientes esfuerzos internos resultan de la integración de los esfuerzos internos de la superficie. Se supone que los sistemas de ejes locales del nervio y la superficie coinciden. Si estos no coinciden, los esfuerzos internos deben transformarse primero en el sistema de ejes local del nervio.
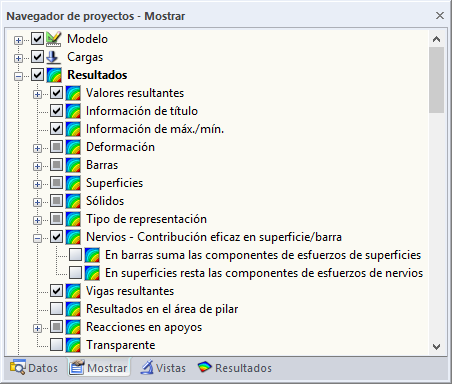
Los esfuerzos internos de la parte del nervio corresponden a los del miembro con una sección transversal del nervio. En RFEM, estos se pueden generar al no incluir los componentes de la superficie para la evaluación de los esfuerzos internos. Los ajustes se pueden realizar en el navegador de proyectos - Mostrar en "Resultados" -> "Nervios - Contribución efectiva a la superficie/barra".
Los esfuerzos internos de la viga en T resultantes del cálculo se obtienen relacionando los esfuerzos internos de la placa y la parte del nervio con el centro de gravedad de la sección transversal de la viga en T.
Por ejemplo, el momento flector de la viga en T resultante sería el siguiente:
My = My,placa + My,nervio - eplaca ∙ Nplaca + enervio ∙ Nnervio
De acuerdo con la configuración predeterminada, los tamaños de paso resultantes de la sección transversal de la viga en T siempre se emiten en el programa.
Nervio en 2D
Básicamente, las vigas en T no son un problema puramente bidimensional. El usuario debe tener en cuenta que la visualización de nervios en 2D va acompañada necesariamente de una simplificación. Dado que la disposición de los elementos excéntricos no es posible en 2D, el eje centroidal de la sección transversal de la viga en T corre en el plano de la superficie. Este enfoque requiere consideraciones adicionales al considerar la rigidez del sistema.
Además de los parámetros del nervio en 3D, existen otros parámetros en 2D para tener en cuenta la rigidez de la sección transversal de la viga en T. La consideración interna del nervio en 2D da como resultado una rigidez solapada en el área de los anchos de integración b1 y b2. Por tanto, una reducción en la rigidez de la superficie en el área del ancho de integración está activa desde el preajuste de los parámetros del nervio. Sin embargo, cabe señalar que debido a este enfoque, la rigidez se concentra a lo largo del eje del nervio, lo que no ocurre en la realidad o cuando el nervio se muestra en 3D.
Dado que una excentricidad no se puede representar en 2D, se tiene en cuenta la influencia de la excentricidad a través de la rigidez, es decir, componentes Steiner adicionales. Para la rigidez a torsión, se superponen la parte de la sección transversal de la viga en T y la superficie. El usuario puede reducir la rigidez a torsión efectiva de la sección transversal de la viga en T. Sin embargo, en principio, no es posible especificar un factor de reducción o un valor porcentual para la rigidez a torsión efectiva, ya que esto depende de la geometría de la sección transversal.
Si está disponible una versión 3D de RFEM, es preferible la versión 2D para la representación de vigas.