此页面有帮助吗？ 1x

238x

009017

2020-06-27

连续荷载作用下薄板的塑性弯曲

项目介绍

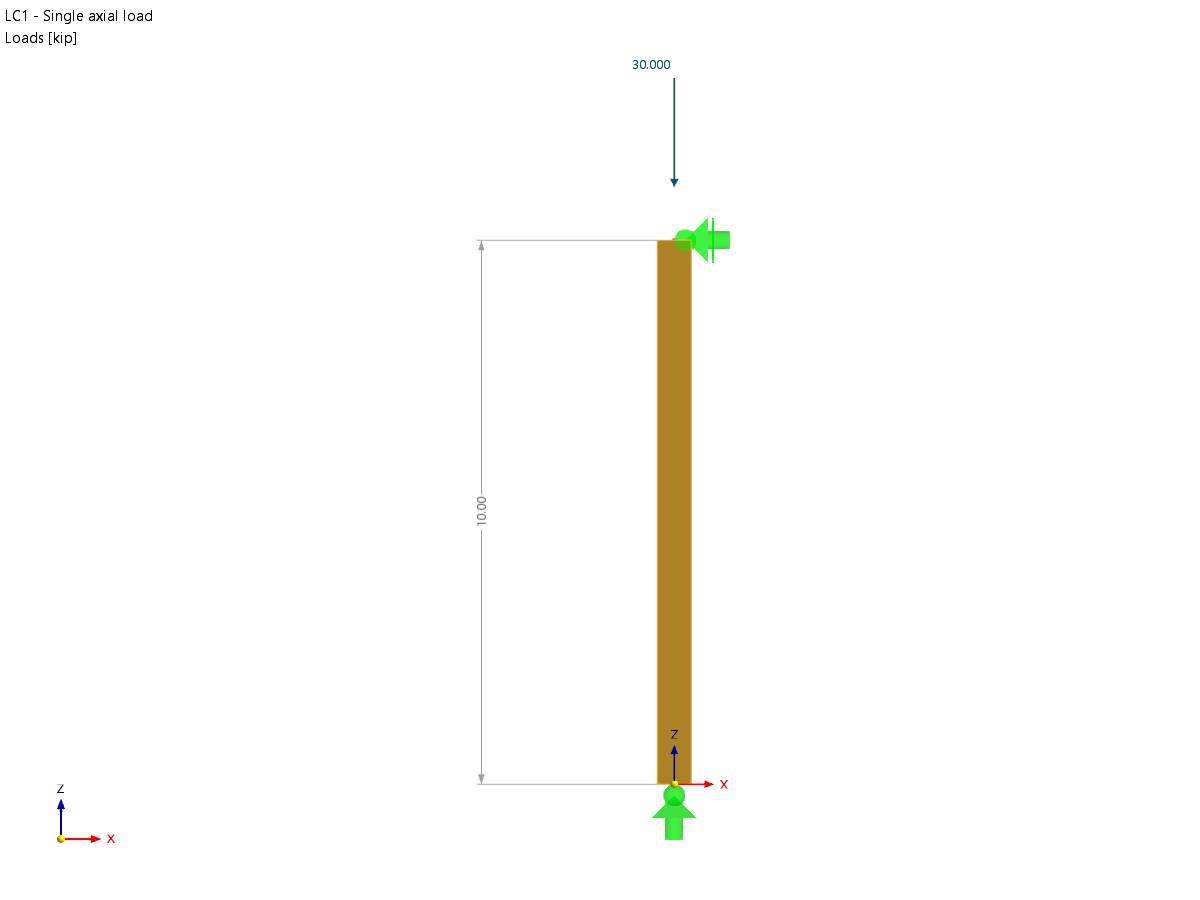
实验中固定一块薄板，左端固定并施加均布压力。这里考虑了小变形，并且自重忽略不计。下面的参数集描述了该问题。计算最大挠度 u_z,max 。

材料	弹塑性	弹性模量	E	210000.000	MPa
		泊松比	ν	0.000	-
		剪切模量	G	105000.000	MPa
		屈服强度	_fy	40,000	MPa
几何尺寸	墙板	周长	L	1.000	m
		宽度	w	0.050	m
		厚度	t	0.005	m
荷载		均匀压力	p	2.750	kPa

塑性弯曲 – 连续荷载

解析解

讨论了荷载的数量。首次屈服时的弯矩 M_e和塑性铰发展时的极限弯矩 M_p计算如下：

M_{e} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w dz = \frac{f_{y} {wt}^{2}}{6}

弹性弯矩

M_{p} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} f_{y} zw dz = \frac{f_{y} {wt}^{2}}{4}

极限塑性弯矩

板在压力 p 作用下进入弹塑性状态。弯曲应力按照下面的公式定义：

σ_{x} (x, z) = - κ (x) Ez

弯曲应力

式中 ka 是曲率。弹塑性区的长度用参数_xp描述。面的弯曲应力等于面上的塑性强度 f_y在点 x_p ，见下面的示意图。

弯曲应力分布

弹塑性弯矩 M_ep （内力）必须等于弯矩 M（外力）。弹塑性区中的曲率 k_p 。

κ_{p} = \frac{1}{E} \sqrt{\frac{\frac{f_{y}^{3} w}{3}}{- \frac{q (L - x)^{2}}{2} + \frac{f_{y} t^{2} w}{4}}}

弹塑性区的曲率

u_{z, \max} = \int_{0}^{x_{p}} κ_{p} (L - x) dx + \int_{x_{p}}^{L} κ_{e} (L - x) dx = 83.117 + 83.117 = 166.234 mm

悬臂梁最大挠度

RFEM 设置

在 RFEM 5.26 和 RFEM 6.01 中建模
单元尺寸 l_FE =0.020 m
实体模型沿厚度方向进行网格细化（每个厚度6个单元）
考虑几何线性分析
增量数目为 5
忽略杆件的抗剪刚度

结果

模型	解析解	RFEM 5		RFEM 6
模型	u_z,max [mm]	u_z,max [mm]	比值 [-]	u_z,max [mm]	比值 [-]
一维各向同性塑性	166,234	166.214	1.000	166.018	0.999
二维/三维各向同性塑性，板		162.987	0.980	162.960	0.980
二维/三维各向同性非线性弹性，板，von Mises		165.730	0.997	165.700	0.997
二维/三维，板，Tresca		166.998	1.005	166.969	1.004
二维/三维各向同性塑性，实体		160.601	0.966	162.429	0.977
各向同性非线性弹性二维/三维，实体，von Mises		163.003	0.981	165.593	0.996
各向同性非线性弹性二维/三维, Solid, Tresca		168.725	1.015	169.691	1.021
一维各向同性非线性弹性		166.214	1.000	166.018	0.999

注释: 解析得出的扭转常数和数值计算得出的扭转常数也是导致结果偏差的原因。

428x

验算示例 0017 | 1

参考

Lubliner, J. (1990)。 塑性理论。纽约： Macmillan 公司。

视频

知识库

KB 001653 | 将第四个节点移动到由三个节点定义的平面中

持续: 00:02:20 min

活动

网络课堂 | 从 RFEM 5 切换到 RFEM 6 | 板件 2

持续: 01:19:08 min

活动

网络课堂 | 从 RFEM 5 切换到 RFEM 6 | 板件 1

持续: 01:06:17 min

常见问题和解答 (FAQ)

FAQ 005343 | 我的旧模型突然变得不稳定。可能是什么原因？

持续: 00:00:21 min

常见问题和解答 (FAQ)

FAQ 005338 | 将模型从 RFEM 导出到 RWIND 时，出现“警告编号...

持续: 00:01:00 min

知识库 001780 | 在 RFEM & RWIND 中进行防风墙多孔织物结构的结构设计

持续: 00:00:47 min

基本

仿生结构是什么意思？

持续: 00:02:14 min

客户项目

CP 001247 | 悬挂和安装 AOD 反应釜的装置的研究

持续: 00:00:20 min

常见问题和解答 (FAQ)

FAQ 005284 | 如何显示或隐藏打印报告导航器？

持续: 00:00:13 min

播放列表

下载模型

61x

3S 缆车上的山顶站

40x

3S 索道 - 中转站 CP 1338

35x

3S 缆车 - 海拔 1600 米的始发站

46x

滑翔机气动性能

156x

San Francisco 教堂虚拟分析

Paintball 场地 ISO 集装箱 RFEM 模型 | © Modular Structural Consultants, LLC.

132x

体育公园集装箱结构

519x

219x

带看台的钢结构大厅

500x

BORA 杜塞尔多夫旗舰店

346x

2025 年世博会捷克国家馆支撑结构

知识库文章

本文着重介绍了膜结构设计的一些具体方面，例如找形和生成裁剪式样。设计这些结构的一个重要步骤是找到合适的预应力形状并生成裁剪式样。本文简要介绍了膜结构设计中的两个基本过程。目的是对其物理性质进行说明，并结合示例进行阐述。

了解更多

本文阐述并解释了索的抗弯刚度对其内力的影响。本文还介绍了如何减少这种影响的方法。

了解更多

知识库 001848 | 在 RFEM 6 中按照 2018 NDS 标准进行木柱设计

使用“木结构设计”模块，可以按照 2018 NDS 标准 ASD 方法进行木柱设计。准确计算木杆件的抗压承载力和调整系数对于安全考虑和设计非常重要。下面的文章将按照 NDS 2018 标准，使用逐步的解析方程验证“木结构设计”模块计算的最大临界屈曲强度，包括受压调整系数、调整后的抗压设计值和最终设计比率。