Пользовательская история
В первом примере мы приступим к предварительному проектированию, уделяя особое внимание расчету общей силы. Выбран квадрат в двумерной плоскости. Он относится к группе 1 WTG-Merkblatt-M3:
- G1: Качественные значения с низкими требованиями к точности для использования в основных исследованиях или предварительном проектировании. Усилия и требования к уровню детализации снижены, так как часто не все граничные условия полностью проясняются.
- R1: Солитарное (без окружающих зданий), анализ отдельных важных направлений ветра.
- Z1: Статистические средние значения, при условии, что они касаются стационарных процессов потока, где колебания (например, из-за приближающейся турбулентности потока) могут быть достаточно учтены другими мерами.
- S1: Статические эффекты. Достаточно представить структурную модель с необходимой механической детализацией, но без учета массы и демпфирующих свойств.
Размеры примера показаны на Рисунке 1, а предположение ввода иллюстрировано в Таблице 1:
Таблица 1: Входные данные примера проверки 2D квадратной плоскости
| Модель | Двумерная квадратная плоскость |
|---|---|
| Размеры | a = 1 м |
| Основная скорость ветра | V = 30 м/с |
| Плотность воздуха | ρ = 1.225 кг/м³ |
| Солвер | На основе давления |
| Модель турбулентности | Стационарная k-ω SST |
| Категория местности | 2 |
| Тип профиля скорости ветра в RFEM | Пиковый |
| Численный алгоритм | SIMPLE алгоритм |
| Дискретизация | Второго порядка |
| Остаточное давление | 10⁻⁴ |
| Кинематическая вязкость | ν = 1.5 × 10⁻⁵ |
В этом примере мы сравним значения силы ветра между EN 1991-1-4 и RWIND. Формула силы ветра в разделе 5.3 Еврокода определяется как:
|
cscd |
Structural factor |
|
cf |
Force coefficient for the structure or structural element |
|
qp(ze ) |
Peak velocity pressure at reference height ze |
|
Aref |
Reference area of the structure or structural element |
Коэффициенты силы (d=b=1 → Cf,0=2.10) прямоугольных сечений с острыми углами и без свободного потока на концах можно получить на Рисунке 7.23 в EN 1991-1-4, а фактор редукции (ψr) для квадратного сечения с закругленными углами (r/b=0 → ψ r=1) можно получить с Рисунка 7.24 в EN 1991-1-4. Указательные значения фактора концевого эффекта ψλ=0.63 как функция отношения плотности φ=1 относительно гибкости λ=2 можно получить на Рисунке 7.36 в EN 1991-1-4.
Коэффициент силы cf элементов конструкции прямоугольного сечения с ветром, дующим нормально на плоскую поверхность, должен быть определен по Выражению (7.9) из EN 1991-1-4:
|
cf,0 |
The force coefficient of rectangular sections with sharp corners and without free-end flow |
|
ψr |
The reduction factor for square sections with rounded corners |
|
ψλ |
The end-effect factor for elements with free-end flow |
- Средняя скорость ветра
Средняя скорость ветра vm (ze) на высоте отсчета z_e зависит от шероховатости местности, орографии местности и основной скорости ветра vb. Она определяется с использованием уравнения EN1991-1-4 (4.3):
- Турбулентность ветра
Интенсивность турбулентности Iv (ze) на высоте отсчета ze определяется как стандартное отклонение турбулентности, деленное на среднюю скорость ветра. Оно вычисляется в соответствии с уравнением EN1991-1-4 4.7. В рассматриваемом случае ze меньше, чем zmin:
- Основное давление скорости
Основное давление скорости q_b — это давление, соответствующее импульсу ветра, определяемое при основной скорости ветра vb. Основное давление скорости вычисляется по основной зависимости, описанной в EN1991-1-4 §4.5(1):
где ρ — это плотность воздуха в соответствии с EN1991-1-4 §4.5(1). В этом расчете рассматривается следующее значение ρ=1.225 кг/м3.
- Пиковое давление скорости
Пиковое давление скорости qp (ze) на высоте отсчета ze включает средние и краткосрочные колебания скорости. Оно определяется согласно уравнению EN1991-1-4 4.8:
Затем сила ветра может быть рассчитана:
Изображение 2 показывает исследование чувствительности сетки в RWIND для 2D плиты. С увеличением плотности сетки от 10% до 40% коэффициент силы Cf уменьшается и стабилизируется на уровне 1.23 от 30% и выше, что указывает на независимость результатов от сетки и обеспечивает точность моделирования без излишней детальной прорисовки.
Также необходимо провести исследование численной сетки в соответствии со следующей ссылкой:
WTG-Merkblatt M3 предлагает два ключевых метода для проверки результатов моделирования. Метод процент попаданий Оценивает, сколько из моделированных значений Pi правильно совпадают с эталонными значениями Oi в пределах заданной погрешности, используя бинарный классификационный подход (успех или промах). Этот подход оценивает надежность моделирования, рассчитывая процент попаданий q, аналогично функциям доверия, используемым в теории надежности. В отличие от этого, метод нормализованной средней квадратичной ошибки (e2) предлагает более подробную оценку точности, количественно оценивая среднее квадратичное отклонение между моделированными и эталонными значениями, нормализованное для учета масштабных различий. Вместе эти методы предоставляют как качественные, так и количественные меры для валидации моделирования.
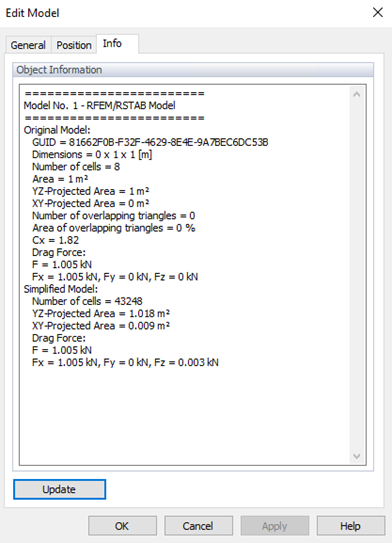
Результаты в RWIND и сравнение с Еврокодом
В RWIND результаты общих сил (на Рисунках 3 и 4) доступны в вкладке Информация в редактировании модели. Разница между RWIND и Еврокодом составляет около Wrel = 2.45% (меньше, чем упомянутые критерии в WTG); тогда процент попаданий может быть получен как q=100%, что показывает хорошее согласие. Низкая нормализованная средняя квадратичная ошибка e2=0.0005 подтверждает сильное согласие между симуляцией и измерениями, что эффективно соответствует стандартам валидации.
Здесь предоставлена 3D модель 2D плиты: