Используемые символы
| h | Высота сечения |
| пролет | |
| E | Модуль упругости |
| модуль сдвига | |
| κ | Поправочный коэффициент сдвига |
| одного | Площадь сечения |
| W | Деформация |
Это связано с низким модулем сдвига и соотношением G/E. Например у хвойных пород из-за анизотропии мы получим 1/16 по {%ref#Refer [1]]]. У изотропных материалов соотношение значительно выше. Для стали, например, соотношение G/E равно 1/2,6.
Теория балок
Тогда как в классической теории изгиба балок Бернулли предполагается, что при деформации сечение стержня остается перпендикулярным оси стержня, то теория балок Тимошенко учитывает скольжение в результате сдвига (балка, подверженная сдвигу). В результате, при деформации сечение стержня уже не будет перпендикулярно оси стержня (см. рисунок 01). Предположим, что сечение остается плоским, тогда мы получим равномерное распределение напряжения сдвига по высоте балки. Поскольку распределение является параболическим, в расчете площадей сдвига учитывается поправочный коэффициент сдвига. Для прямоугольного сечения он составляет 5/6. Таким образом, жесткость прямоугольного стержня при сдвиге равна:
Нормативы
Норма не содержит указаний относительно того, нужно ли учитывать деформации сдвига у стержней или по какому критерию. Следовательно, решение должен принять инженер-проектировщик.
Пример
На простом примере мы покажем влияние деформаций сдвига. Рассмотрим шарнирно опертую однопролетную балку, которая является балкой перекрытия. Подробности показаны на рисунке 02.
Сначала определим только деформацию кривизны момента. У показанной конструкции характерная деформация равна:
Составляющая деформации сдвига может быть получена, например, с помощью данного рабочего метода или принята упрощенно из расчетов {%://#Refer [2]]] или [3]. У однопролетной шарнирно опертой балки мы получим:
Таким образом, общая деформация равна:
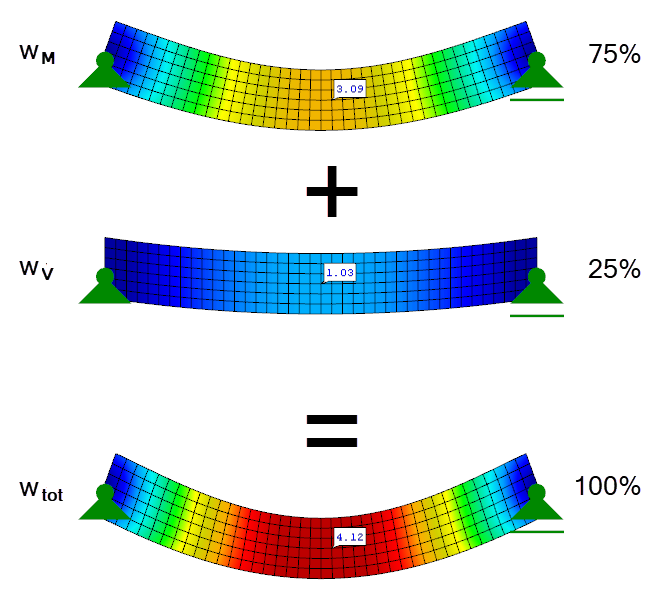
В нашем примере доля сдвиговой деформации уже составляет 25% от общей деформации. На рисунке 03 графически изображены отдельные составляющие деформации.
Гибкость
Гибкость стержня является определяющей для составляющей деформации сдвига. Хотя у продолговатых стержней с высоким соотношением L/h сдвиговые деформации незначительны, они оказывают значительное влияние на компактные стержни с невысоким отношением L/h.
На рисунке 04 на графике показано влияние деформации сдвига на общую деформацию. У шарнирно опертых однопролетных балок с прямоугольным сечением деформация сдвига преобладает при отношении L/h, меньшем или равном 4. После этого преобладает составляющая кривизны момента. После соотношения L/h 12 влияние деформации сдвига на общую деформацию составляет всего лишь 10%.
Статически неопределимые системы
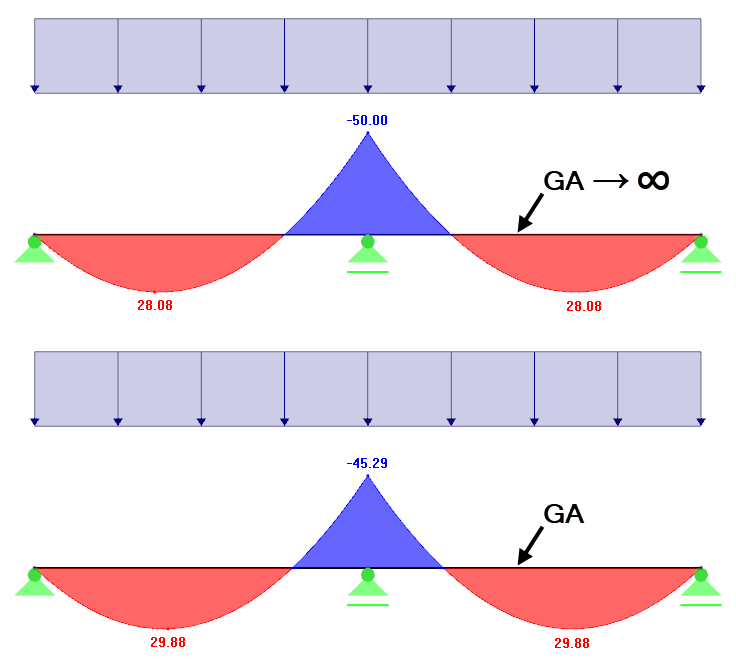
На статически неопределимые системы деформация сдвига оказывает более сильное влияние, чем на статически определимые системы. В данном случае деформации, вызванные силой сдвига, оказывают влияние на изгибающий момент, и соответственно на изгибные деформации. Такое перераспределение может, например, оказать положительное влияние на опорные моменты (см. рисунок 05).
Деформации сдвига в программах RFEM и RSTAB
Деформации сдвига у стержней учитываются в RFEM и RSTAB автоматически. Однако для контрольных расчетов ими можно пренебречь с помощью функции, показанной на рисунке 06. Если отмечено окно флажка, то учитываются деформации сдвига. Если окно не отмечено, то учитываются только составляющие изгибающего момента.
Заключение
Во многих практических случаях деформациями сдвига можно пренебречь, поскольку они не оказывают существенного влияния на общую деформацию. У компактных стержней деформацией сдвига пренебрегать нельзя. В программах RFEM и RSTAB деформация сдвига всегда учитывается по умолчанию, для расчётов вручную необходимо применять инструменты (см. {%ref#Refer [2]]] и {%ref#Refer [3]]]).