Descrição
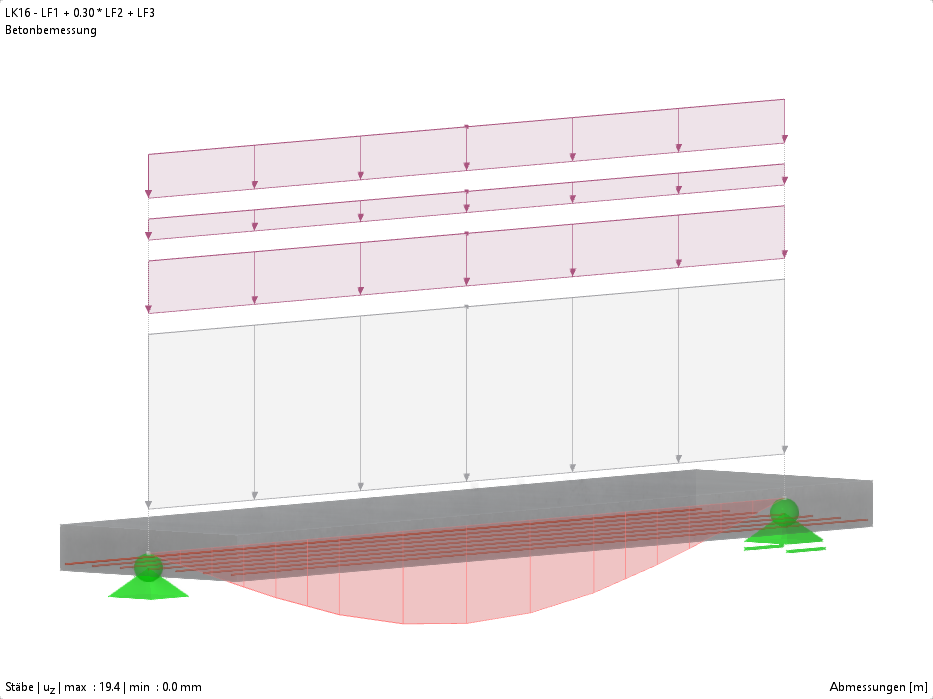
Uma viga em consola feita de um material com diferente resistência plástica à tração e à compressão está completamente fixada na extremidade esquerda e carregada por um momento fletor de acordo com o esboço seguinte. O problema é descrito pelo seguinte conjunto de parâmetros. São consideradas pequenas deformações e o peso próprio não é considerado neste exemplo. Determinar a flecha máxima uz,máx.
| Material | Elástico-plástico | Módulo E | E |
|
MPa |
| Deformação transversal | ν | 0,000 | - | ||
| módulo de corte | G |
|
MPa | ||
| Resistência à tração plástica | bt | 200,000 | MPa | ||
| Resistência plástica à compressão | fC | 280,000 | MPa | ||
| Geometria | Viga em consola | perímetro | L | 2,000 | m |
| Largura | al | 0,005 | m | ||
| Espessura | T | 0,005 | m | ||
| Carga, | Momento fletor | M | 6,000 | Nm | |
Solução analítica
A consola é carregada por um momento fletor M. Devido à diferente resistência plástica à tracção e à compressão o eixo neutro não é necessário coincidir com o eixo da simetria de acordo com a seguinte figura. O parâmetro z0 é introduzido e é definido de modo que σx (x,z0 )=0, tenha em atenção que muda durante o carregamento, bem como os parâmetros zt e zc. A tensão de flexão é definida pela seguinte fórmula:
Para obter a flecha máxima uz,max a curvatura κ tem de ser resolvida. O momento elástico-plástico Mep (força interna) tem de ser igual ao momento fletor M (força externa).
por causa dos parâmetros zt desconhecidos , zc e z0 é necessário escrever outras equações. As tensões na interface entre as zonas elástica e plástica são definidas da seguinte forma:
A última condição é definida pelo equilíbrio das forças axiais.
Resolvendo estas equações numericamente, pode ser calculada a curvatura κ e a deformação máxima uz,max. O resultado pode ser encontrado na seguinte tabela.
Configuração do RFEM
- Modelado no RFEM 5.16 e no RRFEM 6.06
- O tamanho do elemento é lFE = 0,020 m
- A análise geometricamente linear é considerada
- O número de incrementos é 5
- A rigidez ao corte das barras é desprezada
Resultados
| Modelo de material | Solução analítica | RFEM 6 | RFEM 5 | ||
| uz,máx [m] | uz,máx [m] | Relação [-] | uz,máx [m] | Relação [-] | |
| Ortotrópico plástico 2D | 1,272 | 1,277 | 1,004 | 1,277 | 1,004 |
| Isotrópico não linear elástico 1D | 1,272 | 1,000 | 1,272 | 1,000 | |
| Não linear elástico 2D/3D,Mohr - Coulomb, Placa | 1,283 | 1,009 | 1,283 | 1,009 | |
| Não linear elástico 2D/3D,Drucker - Prager, Placa | 1,283 | 1,009 | 1,283 | 1,009 | |
| Isotrópico plástico 2D/3D,Mohr - Coulomb, placa | 1,284 | 1,009 | 1,284 | 1,009 | |
| Isotrópico plástico 2D/3D,Drucker - Prager, Placa | 1,272 | 1,000 | 1,272 | 1,000 | |
| Não linear elástico 2D/3D,Mohr - Coulomb, sólido | 1.308 | 1,028 | 1.307 | 1,028 | |
| Não linear elástico 2D/3D,Drucker - Prager, sólido | 1313 | 1,032 | 1.312 | 1,031 | |
| Isotrópico plástico 2D/3D,Mohr-Coulomb, sólido | 1,302 | 1,024 | 1.293 | 1,017 | |
| Isotrópico plástico 2D/3D,Drucker - Prager, sólido | 1,283 | 1,009 | 1,283 | 1,009 | |










..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)









































_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)





-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)