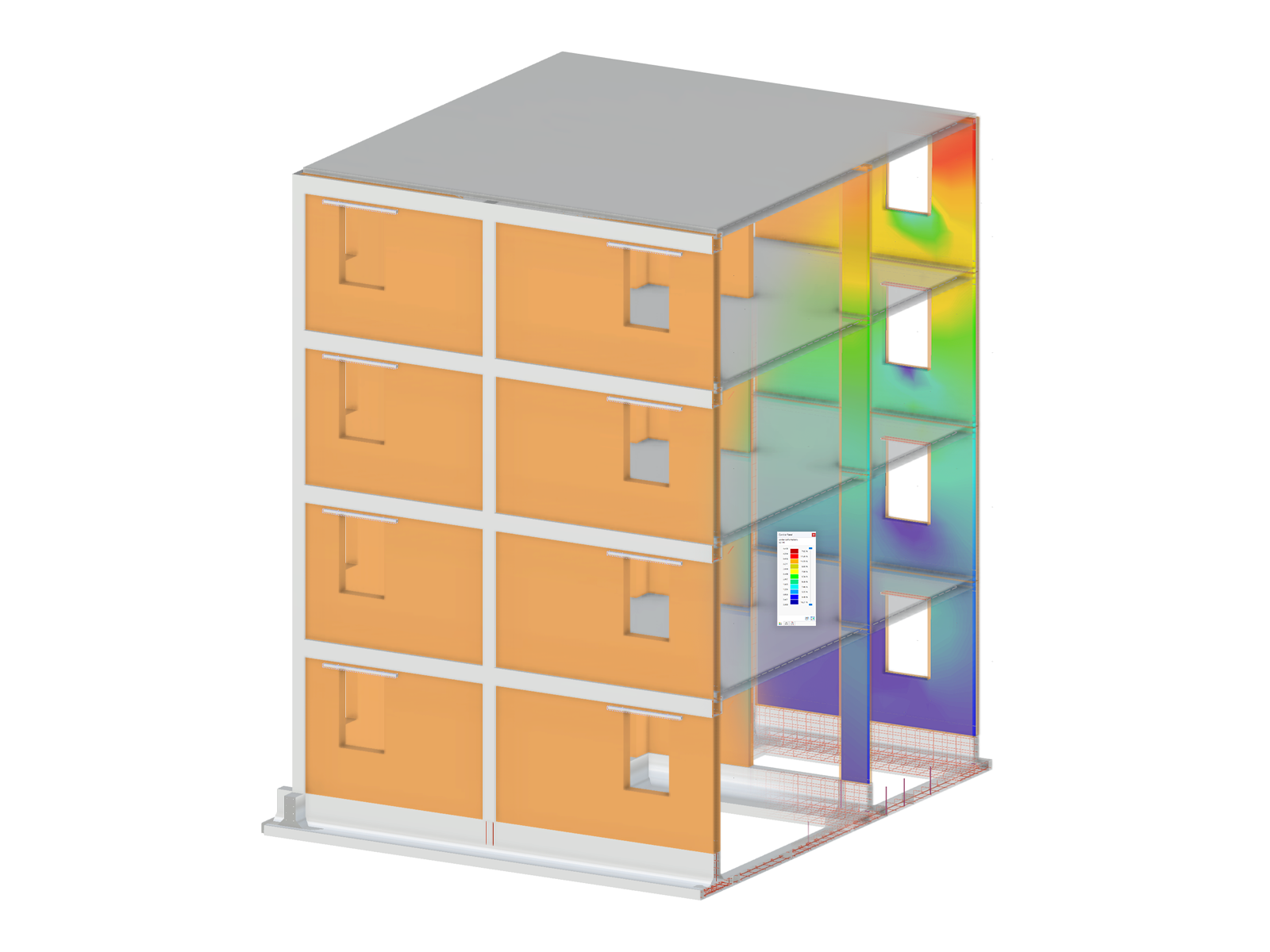
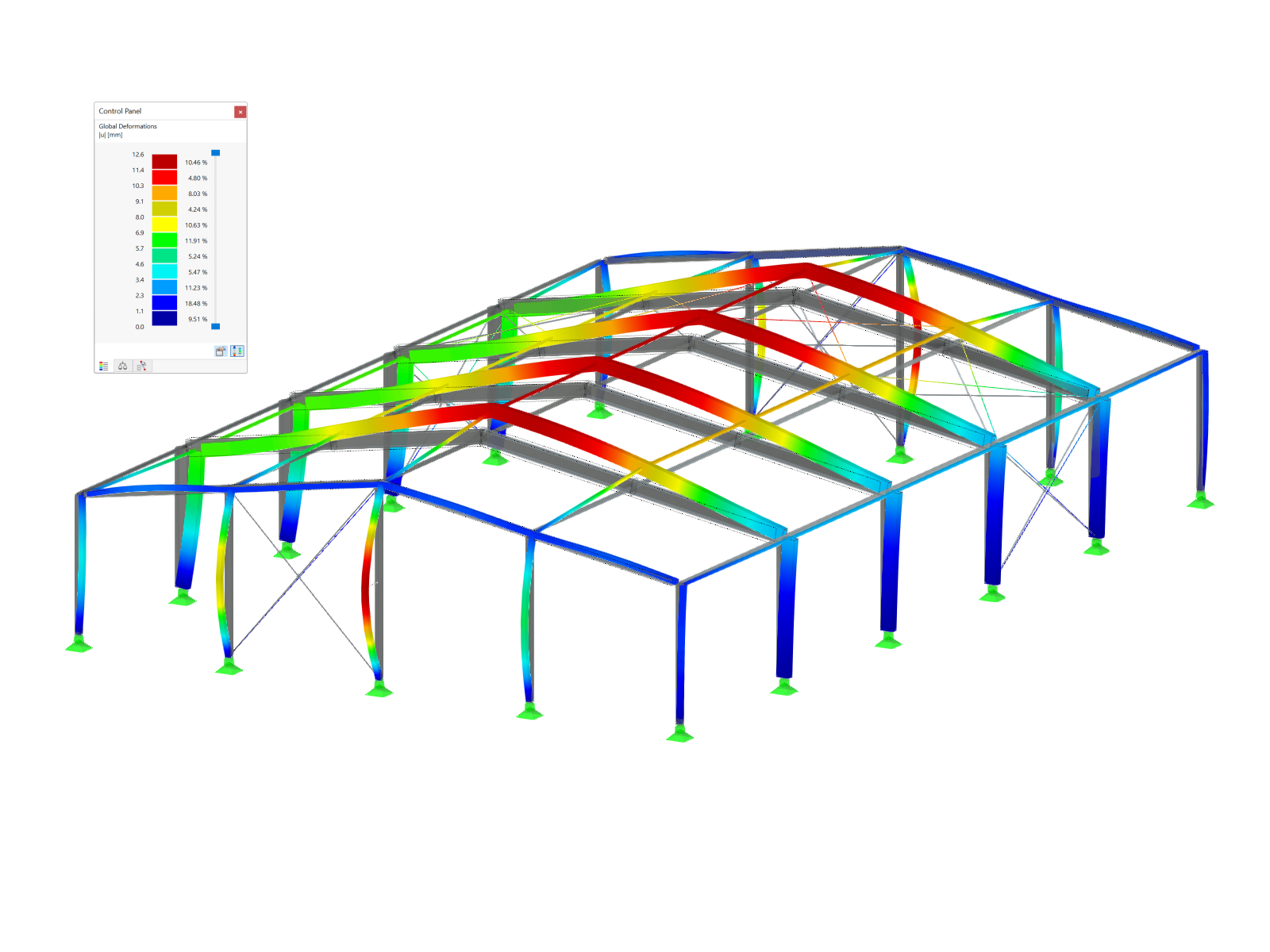
U tenkostěnných ocelových prvků je třeba kromě celkového porušení stability (vzpěr, vzpěr zkroucením, klopení) přezkoumat také lokální stabilitní chování průřezu. V EN 1993-1-3 [1] se rozlišují dva typy:
- Lokální boulení: vyznačuje se boulením jednotlivých částí průřezu mimo jejich rovinu, přičemž se předpokládá kloubové uložení rohů průřezu. Tento typ ohrožení stability je popsán v EN 1993-1-5 [2] jako boulení stěn.
- Boulení celého pole / distorzní boulení: Vyznačuje se vybočením okrajového ztužení průřezu. V sousedních částech průřezu současně dochází k deformacím v rovině a mimo ni.
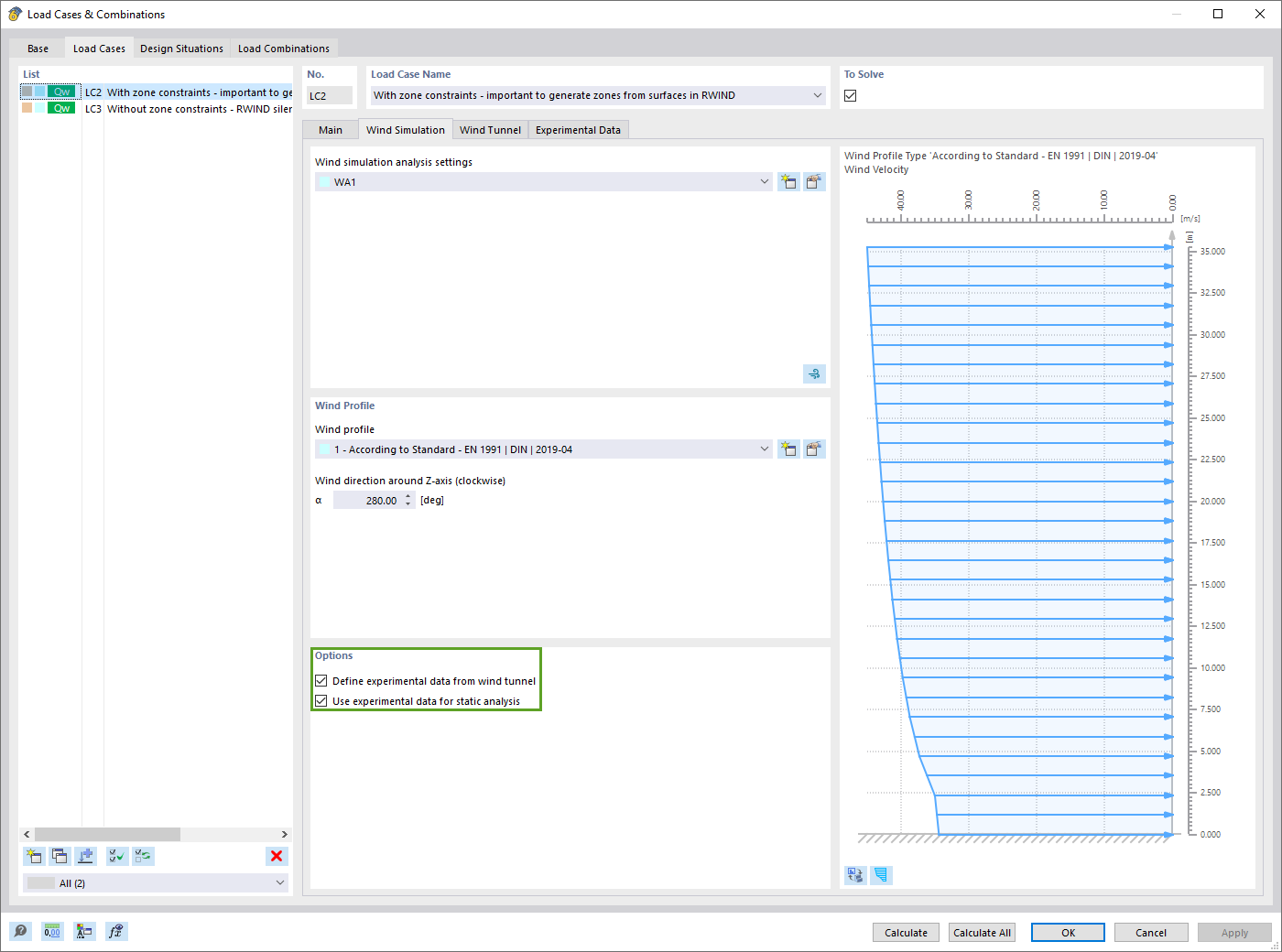
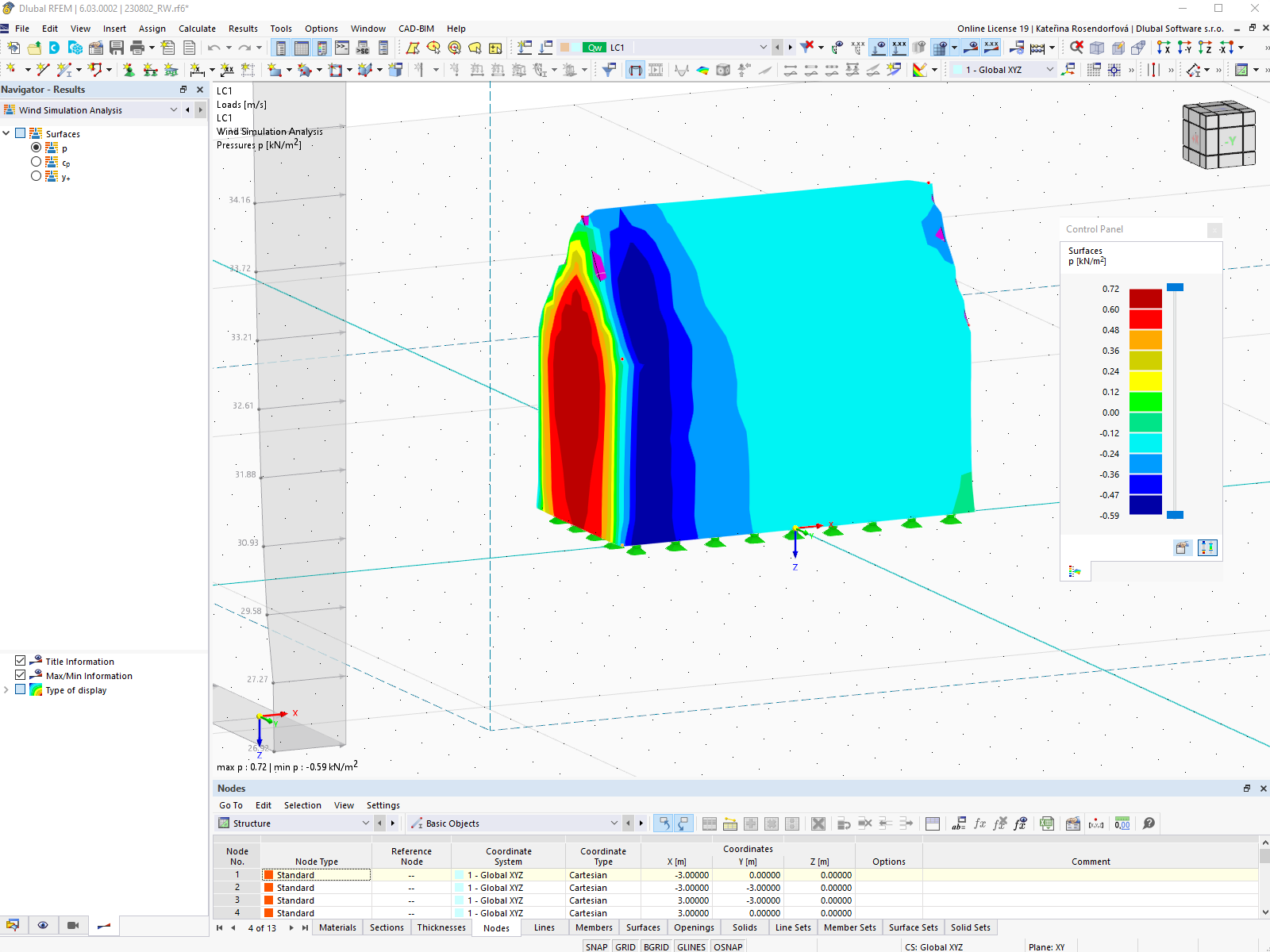
V programech RFEM 6 a RSTAB 9 lze počítat součinitele kritického zatížení a vlastní tvary pro uvedené lokální stabilitní jevy při jednotkovém zatížení. Při výpočtu je použita lineární stabilitní analýza založená na "Metodě omezených konečných pásů (constrained Finite Strip Method - cFSM)" [3]. Výsledky výpočtu metodou konečných pásů lze zobrazit pro všechny tenkostěnné průřezy v dialogu "Upravit průřezy". Kromě jednotkových napětí a dalších průřezových funkcí lze vybrat tvary vybočení v důsledku jednotkového zatížení také z rozbalovací nabídky pod zobrazením průřezu (obrázek 1).
Pokud je zvoleno jedno z jednotkových zatížení, otevře se interaktivní diagram "Výsledky metody konečných pásů". Modrá křivka ukazuje minimální kritickou sílu v závislosti na příslušné poloviční vlnové délce boulení. Výsledky lze také zobrazit odděleně pro různé stabilitní tvary lokálního boulení, distorzního boulení a globálního porušení stability (za předpokladu vidlicově podepřeného prostého nosníku) (obrázek 2).
Je třeba poznamenat, že se v analýze stability zohlední pouze první (jednovlnný) vlastní tvar příslušného stabilitního tvaru. Zjištěné kritické síly však platí také pro násobky příslušných polovičních vlnových délek. To lze doložit srovnáním s výpočtem se skořepinovými prvky v addonu Stabilita konstrukce. Pro analyzovaný C-profil o délce 0,141 m z toho vyplývá kritická síla -90,47 kN, což velmi dobře souhlasí s výsledkem FSM -89,85 kN (viz obrázek 2). Pokud se délka zdvojnásobí na 0,282 m, zdvojnásobí se také počet vyboulení při víceméně stejném kritickém zatížení (-91,68 kN). Pro stanovení rozhodujících kritických zatížení pro lokální stabilitní jevy (lokální a distorzní boulení) by se proto měla vždy zohlednit příslušná minima zjištěných mezních křivek.
Deformace průřezu související s vypočteným kritickým zatížením lze zobrazit v obrázku průřezů. Standardně se zobrazí vlastní tvar, který náleží prvnímu lokálnímu minimu křivky kritického zatížení. Kliknutím na libovolný bod křivky v grafu se zobrazení automaticky aktualizuje. Vlastní tvary na obrázku 4 jasně ukazují vliv příslušných stabilitních tvarů na stanovené kritické zatížení. Zatímco v bodě a dominuje lokální boulení, tvar v bodě b se vyznačuje distorzním boulením. V bodě c je naopak vidět pohyb tuhého tělesa průřezu, který je spojen s globálním porušením stability (zde klopením).
Výsledky FSM umožňují prvotní posouzení stabilitního chování štíhlých průřezů a poskytují informace o tom, zda při porušení stability převládá lokální, globální nebo interakce obou stabilitních tvarů. Ze zjištěných součinitelů kritického zatížení lze také vypočítat mezní únosnost štíhlých průřezů podle EN 1993-1-3 [1] nebo AISI S100-16 [4].
.png?mw=350&hash=b2324c4db119938012b5490afaa56e9aa826cdcc)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
