V tomto příspěvku si ukážeme, jak parametrizovat ztužující prvek buňky příhradové konstrukce znázorněné v modelu.
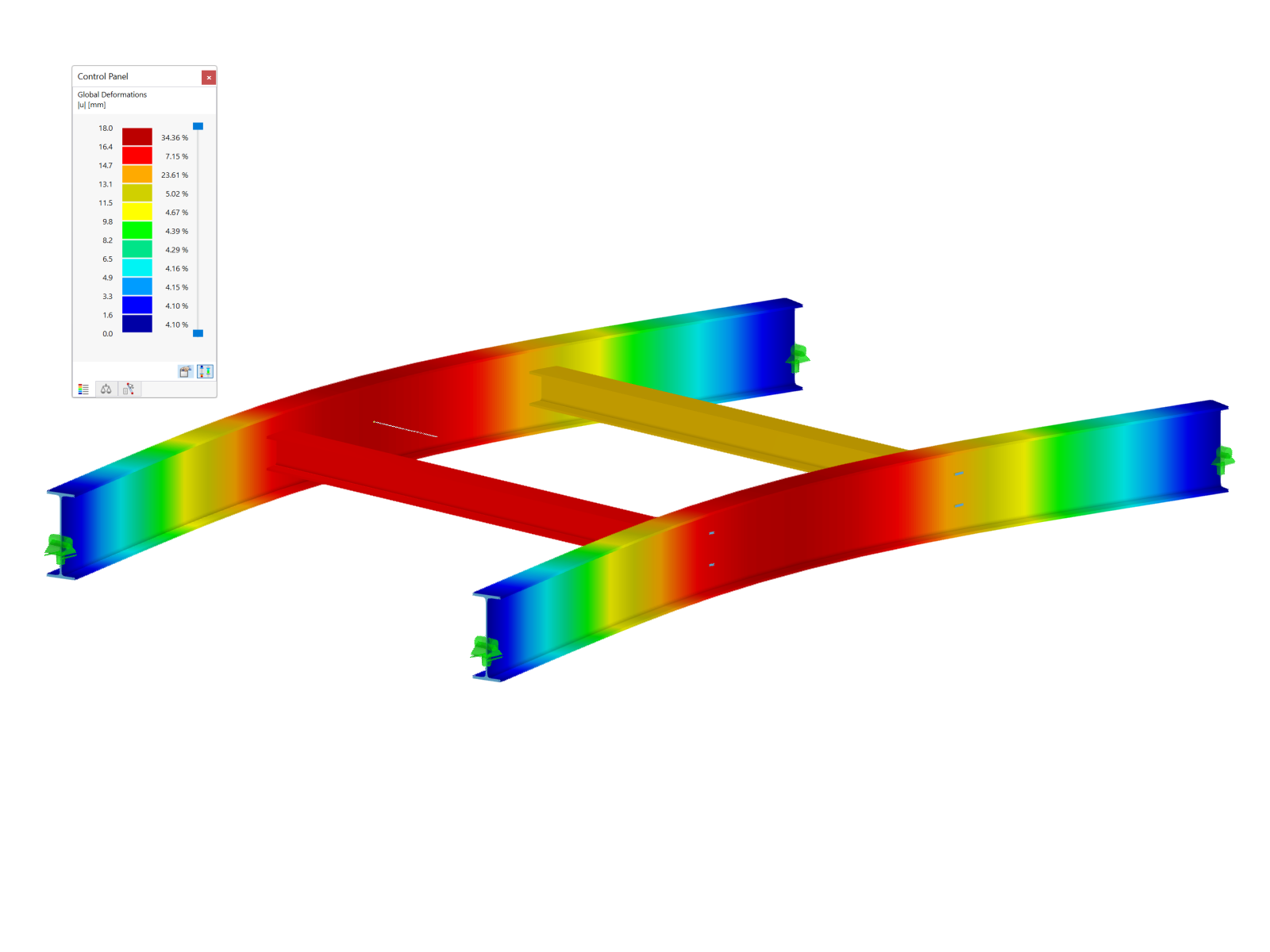
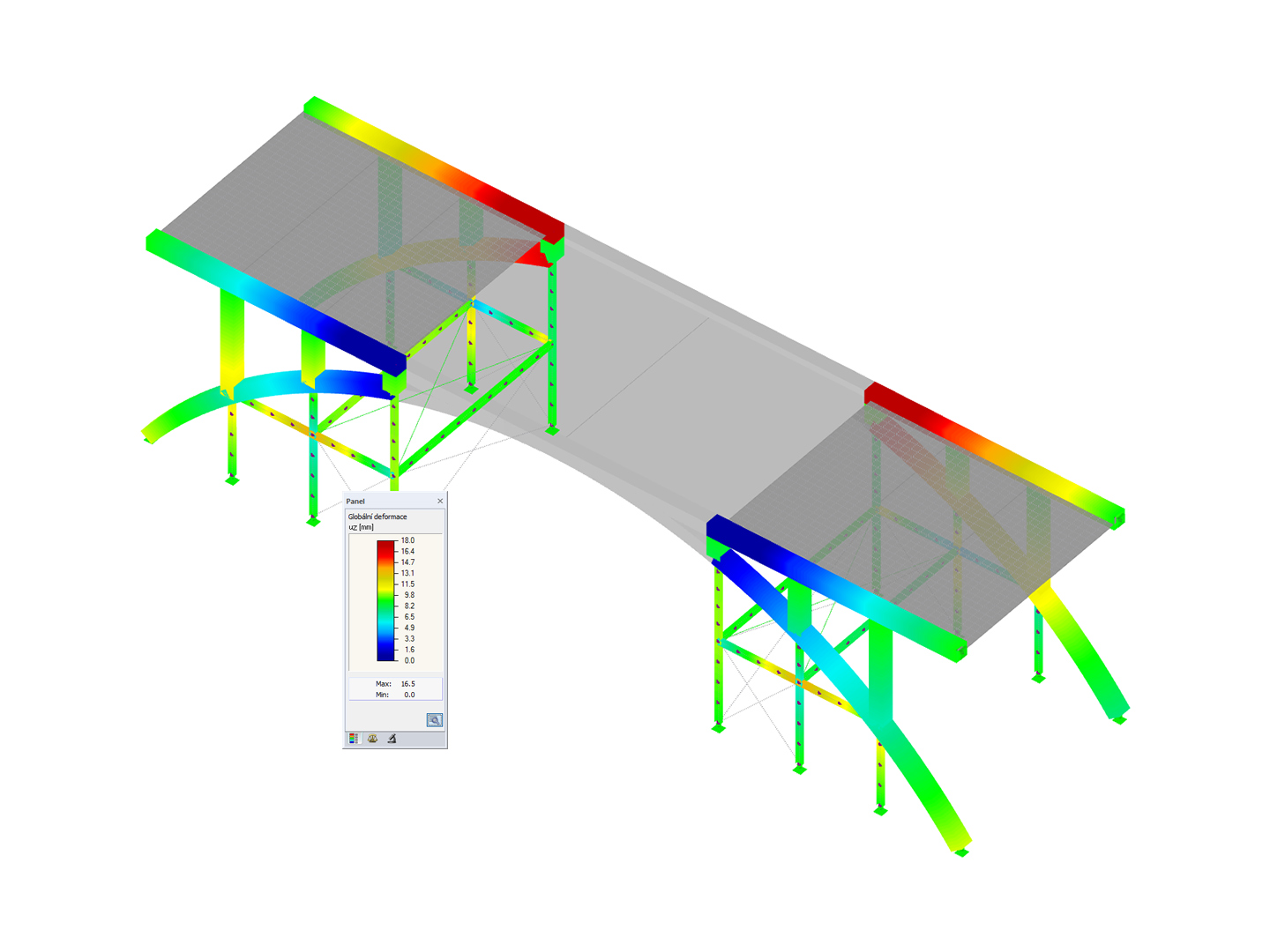
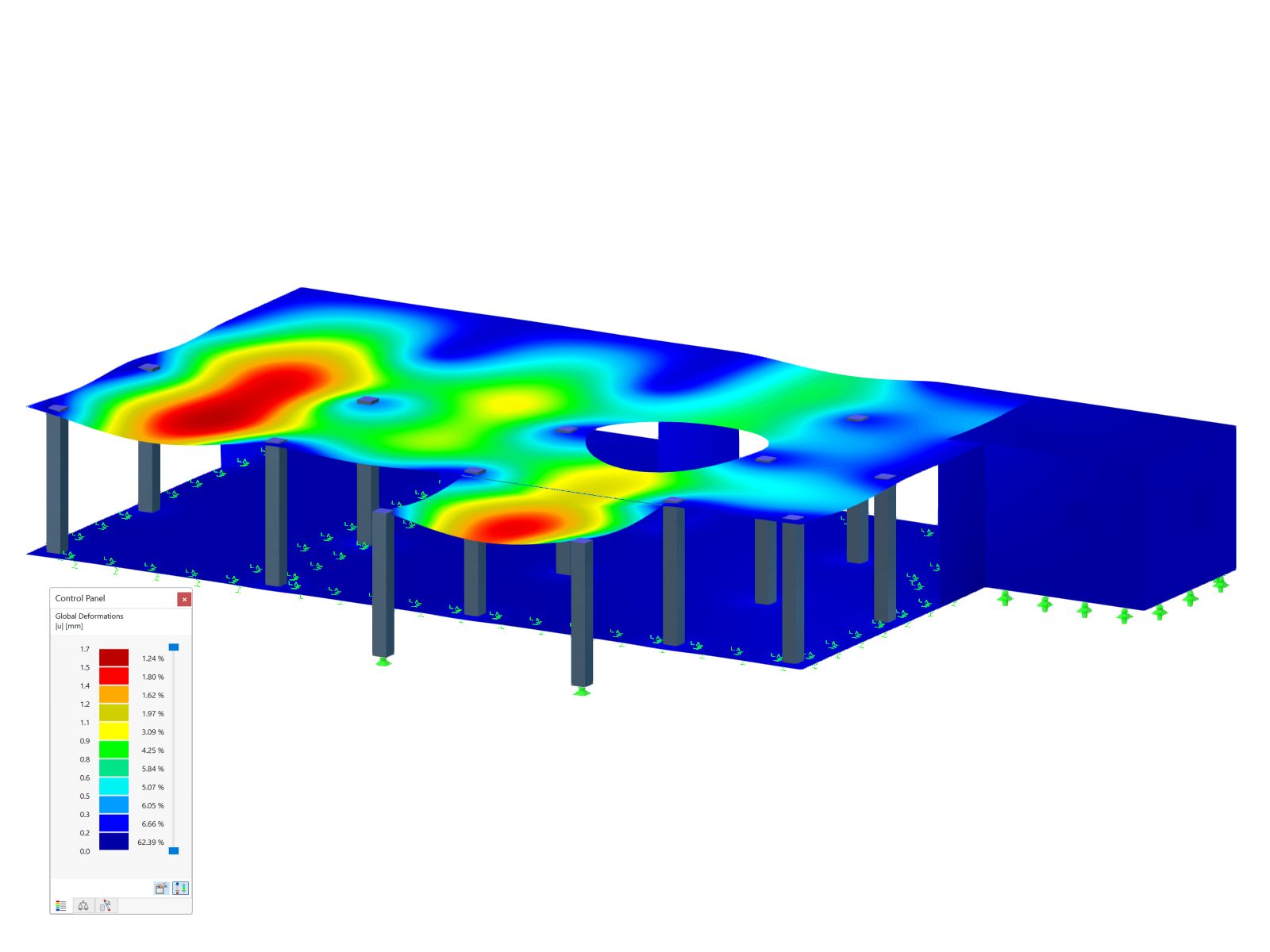
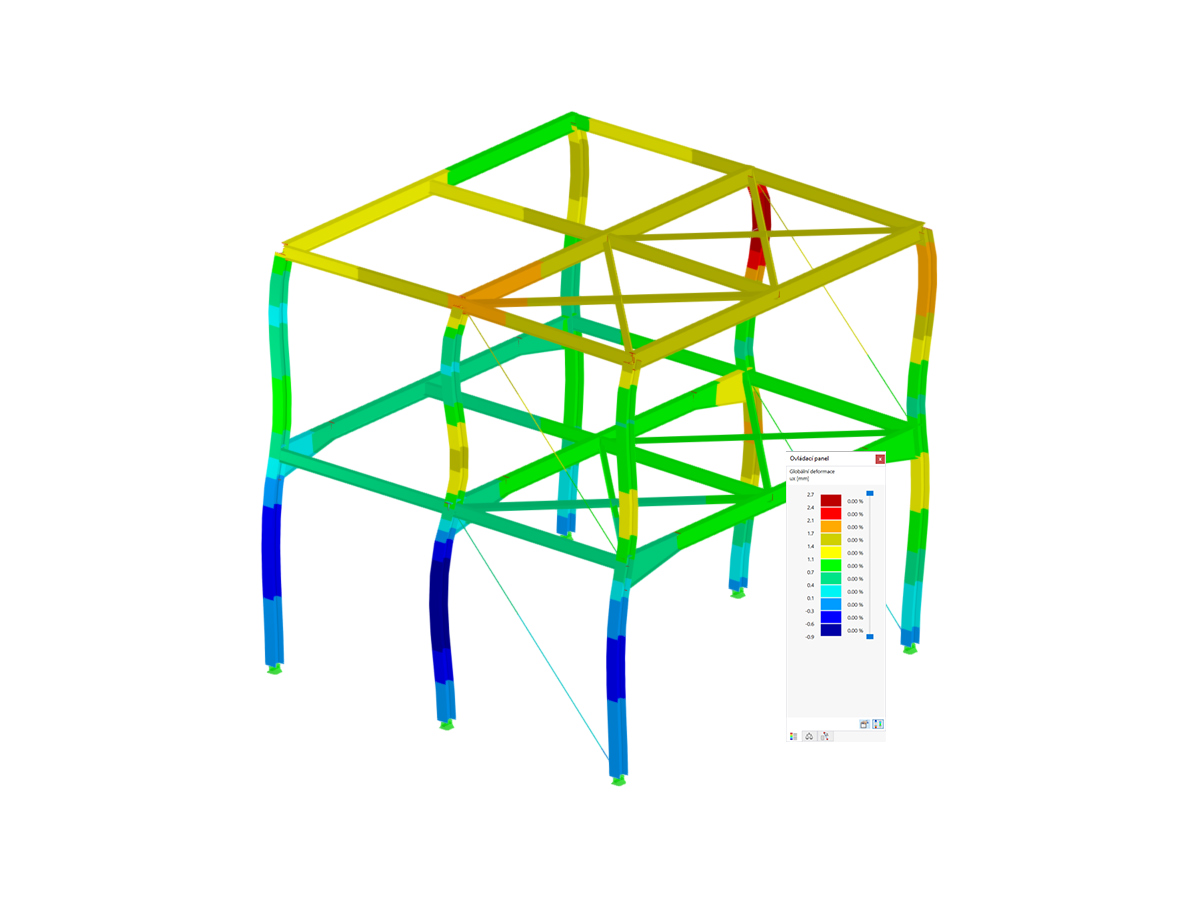
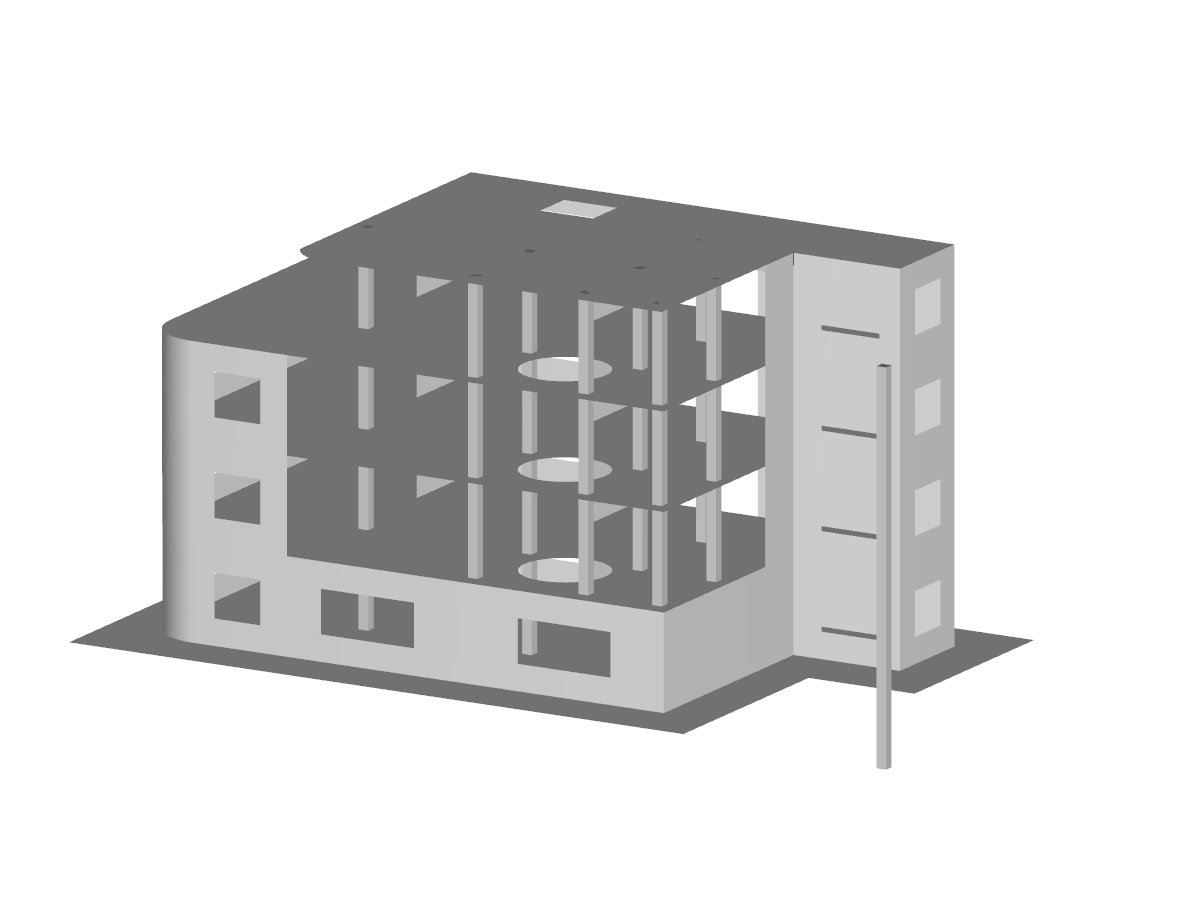
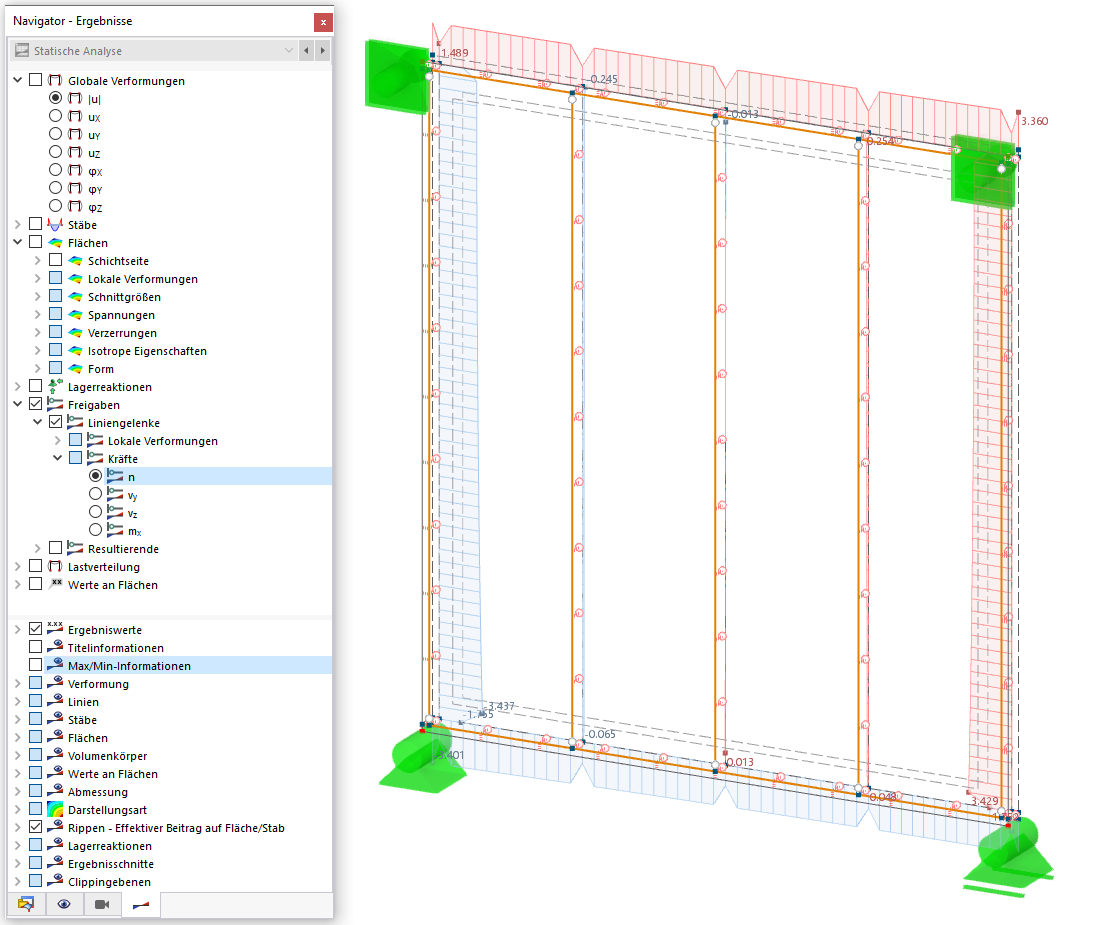
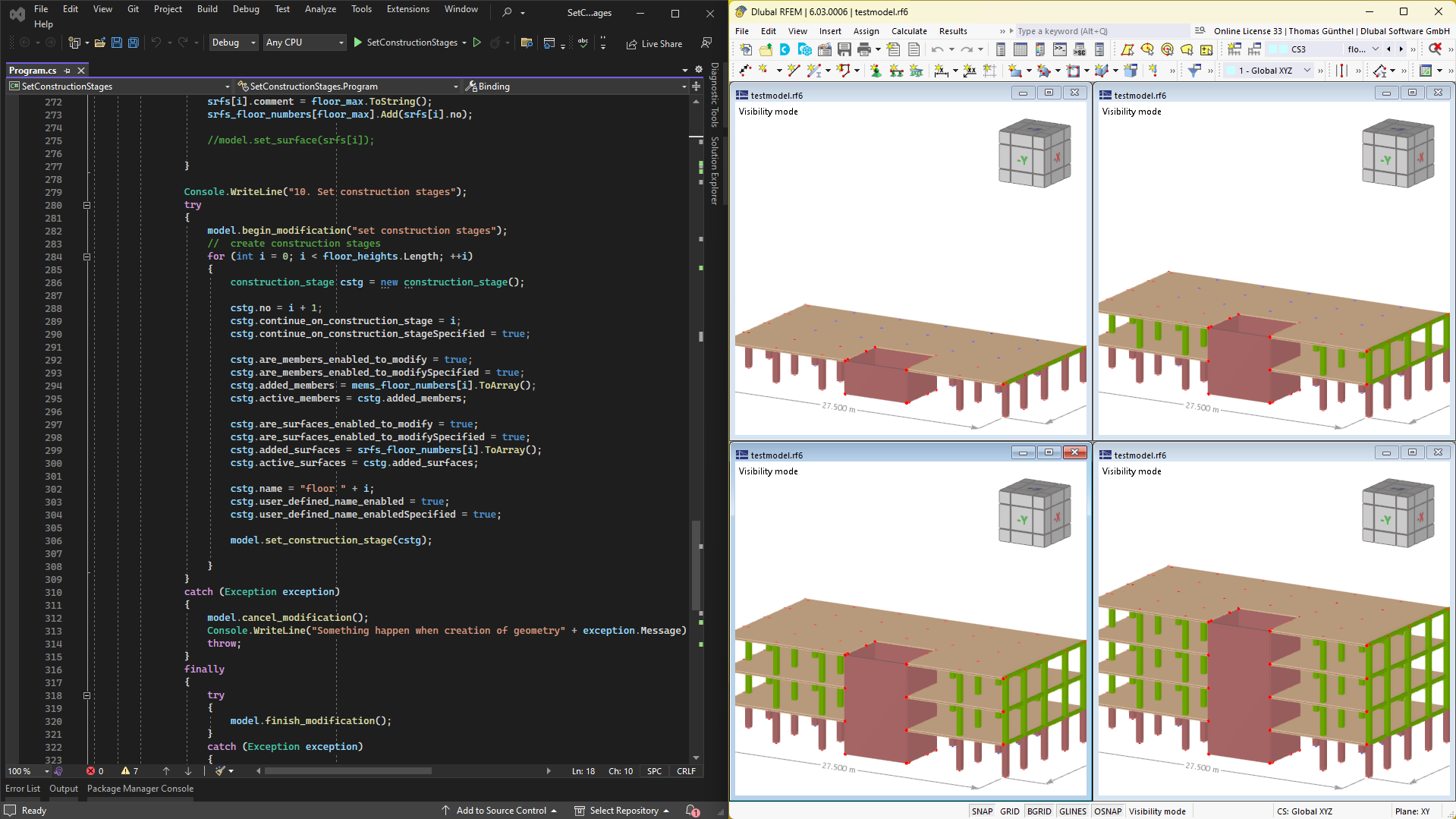
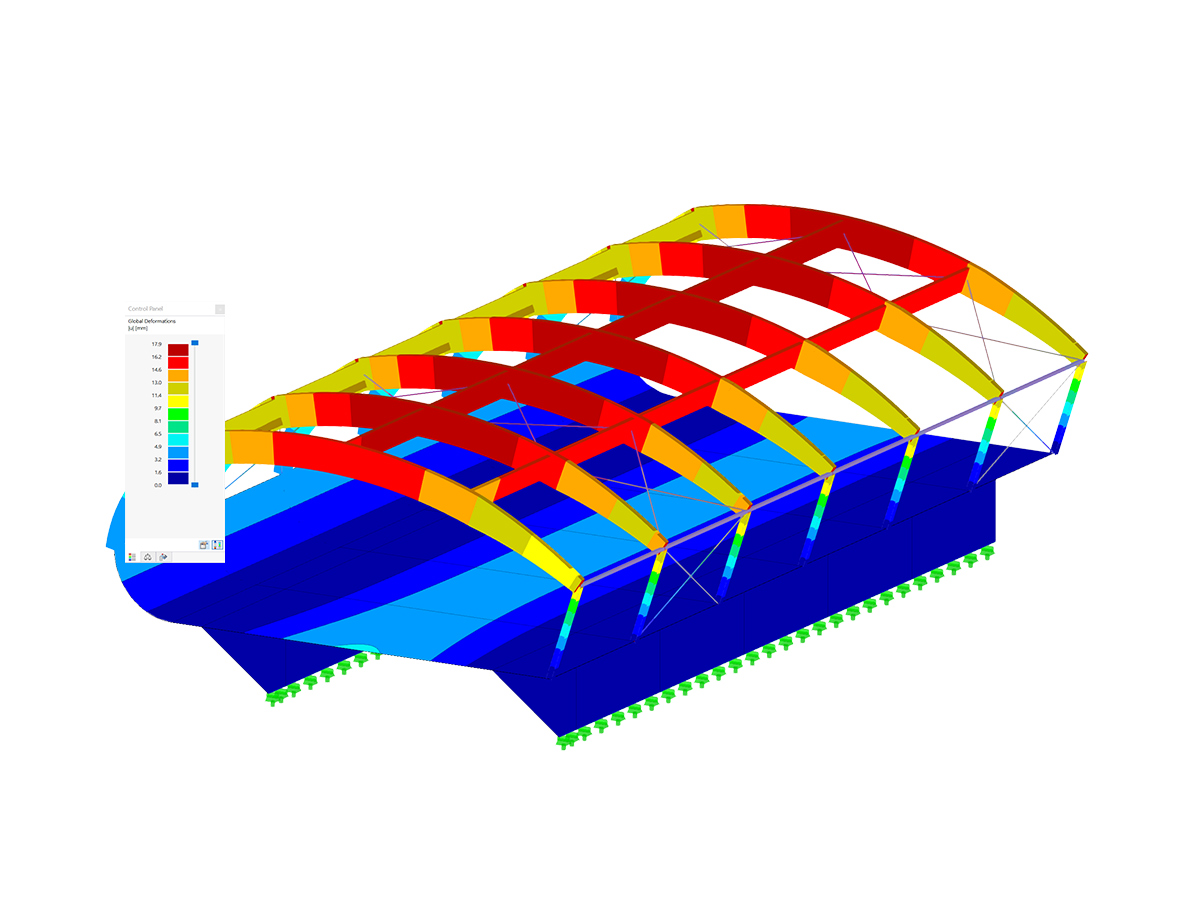
Assuming that the structure has already been modeled in RFEM 6 by assigning members and defining boundary conditions as shown in Image 1, the next step is to define the bracing. Jak jsme již zmínili, definujeme tento prvek pomocí parametrického zadání. Později tak půjde optimalizovat parametry a program automaticky stanoví optimální polohu prvku.
First, you can create intermediate nodes on both the top (Member 2) and bottom (Member 3) chords and connect them with a simple line. Tyto uzly zadáme tak, že klikneme pravým tlačítkem myši na jednotlivý prut a vybereme Dělit prut → n vnitřních uzlů. It is important to create the nodes without literally dividing the members; therefore, you should select the associated check box as shown in Image 2.
Tak je pak ve vlastnostech uzlu vidět, že je typu „Na prutu“ a prut zůstává jedním celým prvkem. Protože byl prut rozdělen jedním vnitřním uzlem, činí relativní vzdálenost mezi vytvořeným uzlem a počátečním a koncovým uzlem prutu 50%. Tato vstupní pole jsou ovšem interaktivní a kromě této relativní specifikace lze hodnotu zadat také v absolutní vzdálenosti (tedy délkou).
Nyní můžeme začít přiřazovat parametry pomocí nabídky Úpravy → Globální parametry. Proměnné, které definujeme, jsou ze skupiny jednotek "Délky", protože nás zajímá umístění ztužujícího prvku, který je reprezentován polohou svých uzlů na horním a dolním pásu.
Hence, you can define the parameters as shown in Image 4; one for the upper (Xtop), and another for the lower chord (Xbottom). Tímto způsobem se stanoví poloha uzlů daná určitými hodnotami přiřazenými těmto parametrům.
Jakmile jsou parametry definovány, lze je použít ve vzorcích pro stanovení číselných hodnot. To je možné provést v dialogu "Upravit" jednotlivých uzlů, kde můžete pomocí editoru vzorců zadat vzorec pro stanovení vzdálenosti uzlu od počátečního uzlu prutu.
For instance, the equation shown in Image 5 indicates that this length will be calculated as the value of the parameter Xtop added to 0.5 m. Given that Xtop was initially set to 0, the equation results in 0.5, meaning that the node will stay at a distance of 0.5 m (Image 6).
Výhodou parametrického zadávání je, že pokud se změní parametr v seznamu parametrů, změní se výsledky všech vzorců, které tento parametr používají. Thus, if you reopen the Global Parameters list and set the value of Xtop as 0.1, the distance of the node with respect to the start node of the member will automatically change to 0.6 (Xtop + 0.5) and the node will be moved as shown in Image 7.
You can go a step further and utilize other advantages of the formula editor, such as inserting an object property in the equation, as shown in Image 8.
Pomocí příslušné ikony otevřeme rozsáhlý seznam vlastností objektů a jejich podkategorií a vybereme tu, která nás zajímá. Například můžeme vybrat coordinate_1, což je kartézská souřadnice X uzlu. You can indicate the associated node in the formula text box, as shown in Image 9.
In this example, we are interested in calculating the distance of Node 5 with respect to the X coordinate of Node 3. This means that if Node 3 is displaced and its X coordinate is changed, the position of Node 5 will be automatically modified, since this object property is included in the formula.
V tomto článku jsme ukázali, jak lze definovat globální parametry a jak je používat ve vzorcích pro stanovení číselných hodnot. I tyto parametry lze optimalizovat podle různých kritérií, což bude námětem pro náš další článek databáze znalostí.
Databáze znalostí