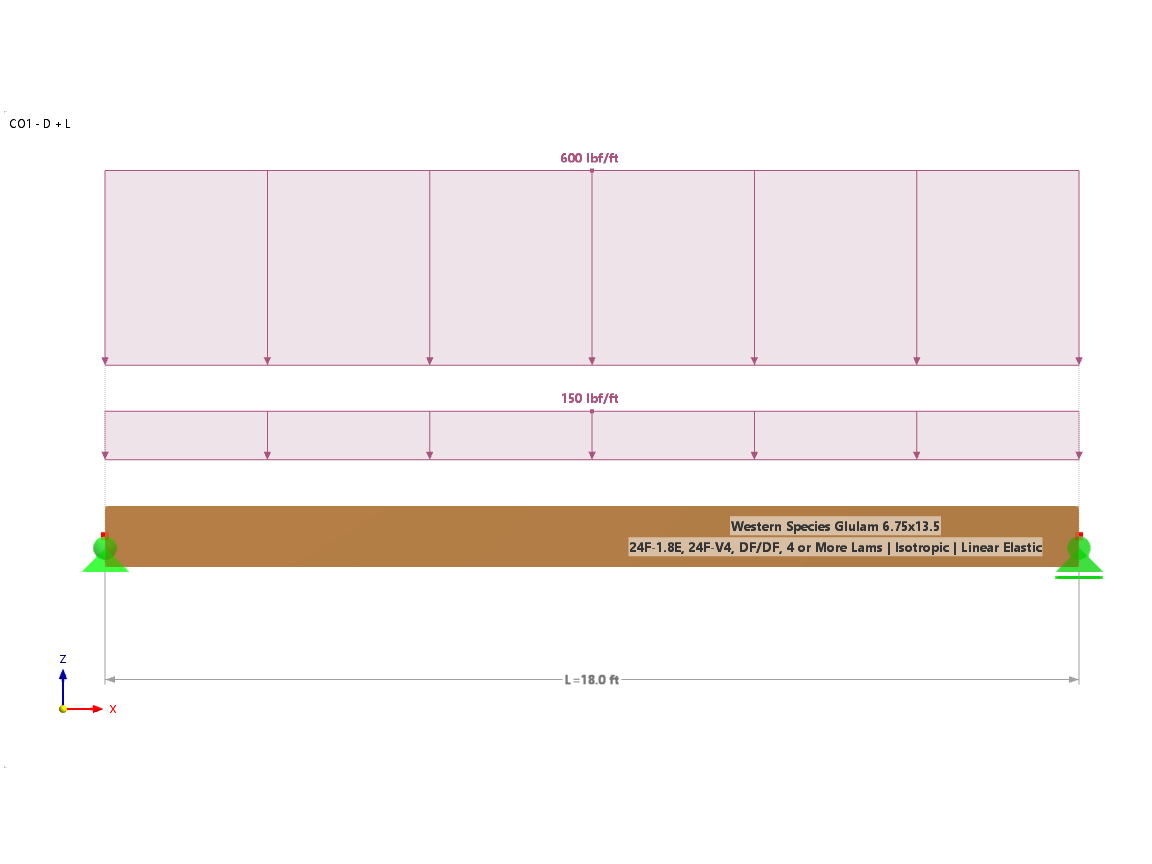
本文将使用三维木结构进行建模, 木杆拱的净跨度为 65 米,从底部到拱顶的高度为 16 米。
雪荷载按照 ASCE 7-22
规范中的图 7.4-2 [1] 清楚地显示了在平衡和非平衡雪荷载下如何加载弯曲屋面。 沿拱长方向向下施加的雪荷载根据特定位置处的屋面坡度而变化。 因此必须沿着拱的整个长度来确定倾角。
确定屋面倾角
将拱形屋顶的立面视图转换为线单元并投影到 x 和 y 坐标系上,x 坐标点沿结构底部,每次确定的增量为 1 英尺。 这个结构例子中的拱只是一个圆的一部分,那么可以使用圆的方程来计算拱的长度。
重新排列上面的公式,因为除了拱的 y 坐标之外所有的值都是给定的,所以公式变成:
要求圆弧上一点的斜率,必须对圆关于 x 的方程应用隐式微分。
求解隐微分,由 dx/dy 表示的斜率 rise/run 如下。
要确定以度为单位的斜率,请应用正切功能。
此外,在斜率公式中可以代替上面的 "y" 公式,因为与已知的 x 坐标点相比,可能不是很容易知道该值。 现在可以沿每个 x 位置确定拱形结构的倾角,单位为度。
雪荷载大小
按照图3. 见章节 7.4-2,根据屋面边缘或屋檐处弯曲的屋面几何形状,存在三种不同的情况。
- 屋檐处弧形倾角 < 30°
- 屋檐处弧形倾角 30° 到 70°
- 屋檐处弧形倾角 > 70°
对每种情况都沿拱的长度方向同时施加平衡和非平衡荷载。 作用在倾斜表面上的雪荷载是应用在表面的水平投影上。 图 7.4-2通过将屋面雪荷载pf 乘以屋面坡度系数Cs来总结这些荷载值。 Cs考虑了沿拱长的变化坡度,并且取决于图7.4-1中所示的几个系数{%! %!
暴露系数 Ce是用来确定拱形结构倾角在 30° 和 70° 之间变化的位置处的雪荷载大小,如图 4 所示。 公式 7.4-2 仅适用于不平衡荷载工况。 根据地形类别和屋面暴露的条件,该值可以从表 7.3-1 {%于#参阅 [1]]] 中确定。
平屋面雪荷载按照公式 4.5 计算。 7.3-1 [1] 如下所示。
pf = 0.7 ⋅ Ce ⋅ Ct ⋅ pg
其中 Ce和 Ct在上面已经讨论,并分别在表 7.3-1 和 7.3-2 中找到。 地面雪荷载pg见图1。 7.2-1 {%!
Dlubal 软件公司将 ASCE 7-22 中的地面雪荷载分区图与谷歌地图集成在一起,制成了德儒巴网站上的分区工具。 使用此工具,用户可以输入项目地址或直接点击地图出现。 荷载查询工具将根据规范 ASCE 7-22 自动显示指定地点的雪荷载分区、风荷载分区和地震分区。 与手动查找规范中的信息相比,这种方法可以更有效和更简单地确定美国不同地区的地面雪荷载。
雪荷载位置
对于所有三种弯曲屋面的雪荷载,其大小沿拱长方向变化,具体取决于屋面的坡度,如图 4 所示。 7.4-2。 这三种情况下所需的主要位置是 70°、30° 和路拱。 使用上面的 坡度公式 可以很容易地沿着拱长度确定这些特定的点。 这些特定位置点之间的大小线性变化,因此不需要评估每个坡度点的雪荷载大小。
对于平衡荷载情况,拱形左侧和右侧的大小设置为 Cs ⋅ pf,其中 Cs = 1.0。因此,用户需要根据图7.4-1 确定在哪个相应的屋面坡度位置,Cs系数等于1.0。确定屋面倾角后,可以根据坡度公式中的信息找到沿拱长的点。
在荷载不对称情况下,迎风面可以认为没有雪。 雪荷载只施加在拱背风面,如荷载图中所示。 当前屋面与另一个屋面相邻,图中还显示了在荷载大小和荷载位置的不对称荷载工况中如何考虑这些特殊情况。
在 RFEM 6 中的应用
借助 RFEM 6 中提供的工具可以轻松处理复杂的荷载工况。 要想沿上述初始公式所示的拱长计算所有位置的屋面倾角,最简单的方法是使用电子表格程序,例如 Microsoft Excel。
利用计算出的屋面倾角和上述确定 ASCE 7-22 中雪荷载大小的步骤,可以在 Excel 中简化计算,例如屋檐, 70°, 30°,和表冠。 该信息可以在一个电子表格中定义为表格格式,其中x位置沿拱形投影x轴定义,以及相应的雪荷载大小。 下面是该示例中使用的 Excel 电子表格的链接。
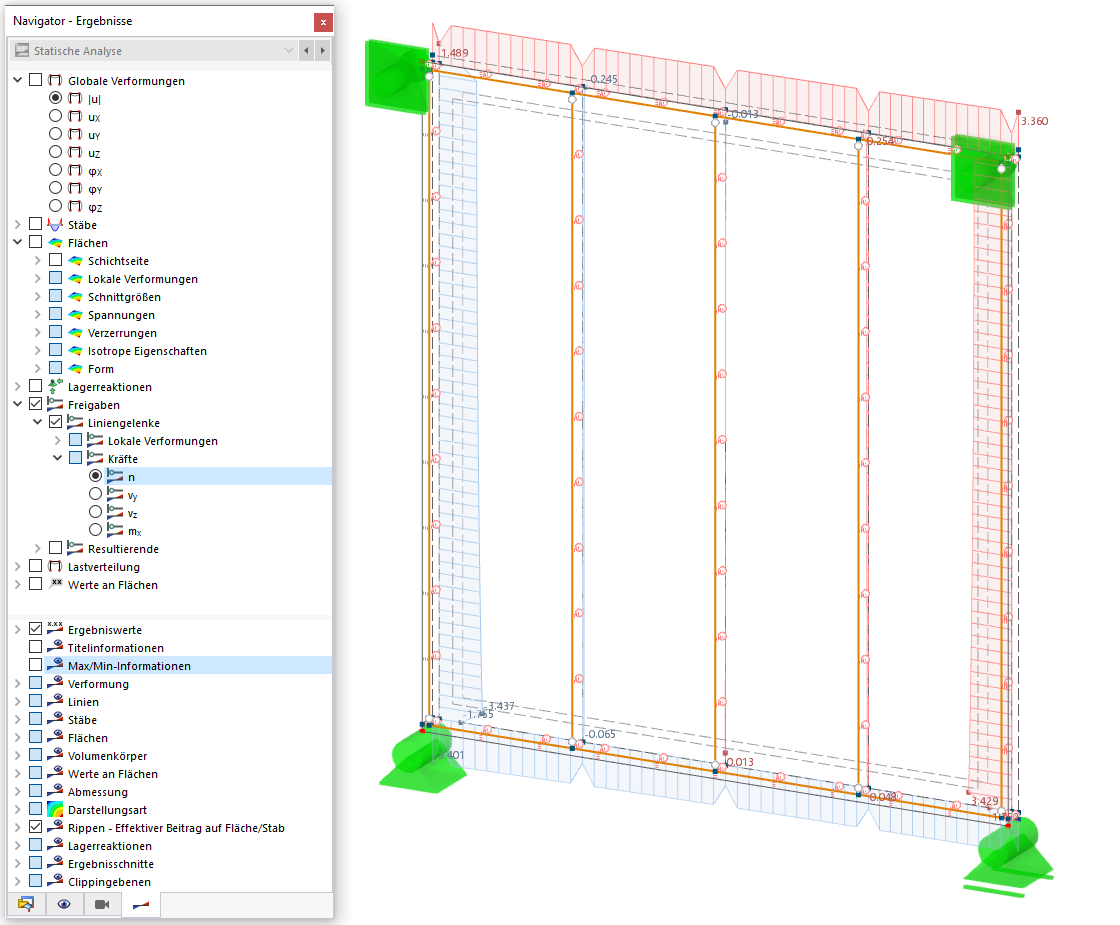
在 RFEM 6 中选择“新建杆件集荷载”按钮将荷载施加到杆件集上。 荷载分布为“可变”的荷载分布将在投影的 Z 方向“ZP”上使用。 此外,点击“编辑可变荷载”按钮可以激活程序内的表格。 只需点击一下鼠标,活动 Excel 工作表中当前定义的所有信息都可以直接导入到 RFEM 6 的表格中。
对于 RFEM 中的单独荷载工况可以按照相同的方案进行不平衡的雪荷载。
从 Excel 中直接导入可变荷载的功能对于多杆件荷载的应用以及荷载大小沿杆件长度变化很大的情况非常有用。







..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)