AISC 钢结构设计指南 26 – 抗爆结构的设计 {%!简化爆炸设计荷载的应用。
理想化爆炸荷载压力-时间曲线
理想化的压力-时间历程曲线图显示了爆炸发生后压力随时间的变化。
图中直接列出了一些最重要的参数，其中包括：
- 峰值超压（Pr或 Pso ）...到达结构的瞬时压力，高于环境大气压力。
- 正相持续时间 (td ) …压力恢复到环境压力的时间段。
- 正脉冲 (I) … 在正的持续时间内施加的总的压力-时间能量，通过曲线下的面积计算。
- 负压阶段的持续时间 (td- ) … 进入正压阶段后的时间，在此过程中压力低于大气压。
请注意，在理想压力-时间曲线图中显示了两条不同的曲线，分别是“爆炸荷载侧面”和“反射爆炸荷载”时的虚线和实线。 侧面爆炸荷载（也称为自由场爆炸荷载）在文献中通常使用下标“so”。 这表示爆炸荷载平行于面的位置，而不是垂直于面的位置。 本质上，荷载将扫过没有阻挡的物体。 例如一面平行于爆炸的墙或没有直接爆炸的后面。
反射爆炸荷载由下标“r”表示，是指爆炸波到达一个倾斜的表面，而不是平行的。 计算反射压力 Pr ，可以使用下面的公式。
Pr = Cr Pso
式中，Pso为侧面压力，Cr为反射系数。 Cr是迎角和侧面压力的函数。
下图显示了如何在考虑初始爆炸波方向和法线为反射波的情况下计算入射角。
一旦确定了爆炸角度，就可以按照美国设备规范 (UFC) 3-340-02 – 结构抵抗偶然爆炸效应中给出的图 2-193 的计算方法 {%于#Refer [2]]]用于提供基于峰值峰值超压值的Cr值。
简化的爆炸荷载压力 - 时间曲线
为了便于计算，上面显示的理想曲线被简化为三角形分布，其瞬时上升和正阶段线性下降。 为了保持理想化图中的峰值超压以及脉冲（曲线下的面积），虚拟持续时间 te近似为 te = 2（I/P）。
为了确定装药重量、投射距离（从结构到爆炸的距离）以及压力-时间图中定义的爆炸参数之间的关系，进行了大量的研究。 在技术手册（例如 参考资料 [2] 中）以经验参数曲线的形式介绍了气流冲击参数与比例距离之间的关系。
对于简单的结构，为了简化计算，经常可以忽略负的振型，因为爆炸分析的影响很小。 但是，当结构在反荷载方向上的强度较弱或基本周期大于荷载作用持续时间的作用时，负的周期就变得越来越重要。
本文中未考虑可能影响爆炸分析的其他变量，例如风荷载或动压力产生的拖曳力、相邻建筑物的遮蔽（折减）和反射（放大荷载），爆炸波进入结构洞口时产生的内部荷载。
AISC 设计指南 26 – RFEM 中的示例 2.1
AISC 设计指南 26 – 示例 2.1 {%！ 示例结构是单层钢结构建筑，尺寸为 50 米长 ⋅ 70 米长 ⋅ 15 米高。 在 RFEM 中，在短边方向上有支撑的框架采用热轧 W 形截面建模，在长度方向，刚性框架也是用 W 形截面建模。 桁架和檩条采用热轧 C 型截面。 建筑外立面采用了肋形金属板。
爆炸荷载为 500 磅，发生在距离建筑物正面 5 米处，略微高于地面。 利用此信息，可以根据以下公式计算缩放距离 Z。
前墙
根据该比例距离，可根据图 2-15 中 [2] 中有关表 1 中反射压力和侧面压力的正的爆炸波参数直接计算。
| 爆炸荷载参数 | 由图 2-15 {% |
|
计算值 |
|---|---|---|
| 反射压力峰值 (+) | Pr = 79.5 psi | - |
| Side-on 峰值压力 (+) | Pso = 24.9 psi | - |
| 反射脉冲 (+) | Ir = 31.0W1/3 | Ir = 246 psi·m |
| “侧面”冲量 (+) | Iso = 12.1W1/3 | Iso = 96.0 psi·m |
| 到达时间 | ta = 1.96W1/3 | ta = 15.6 ms |
| 指数荷载持续时间(+) | td = 1.77W1/3 | td = 14,0 ms |
| 激波前缘速度 | U = 1.5 m | - |
因为前墙体直接面向初始爆炸，所以表 1 中的“反射”变量适用于该面。 简化三角形法需要计算等效持续时间，以确保冲量（曲线下面积）在持续时间为正的阶段中保持不变。
te,r = 2Ir/Pr = 2(246 psi·ms)/29.5 psi = 6.19 ms
前壁面的初始压力-时间曲线现在已完成。
墙面和屋面
为简单起见，将在正面计算的距离 Z 用于确定建筑物侧墙和屋顶的爆炸变量。 因此，建筑物侧面朝上的数值用于定义压力-时间曲线。 在进一步的计算中，冲击波的折减量与墙体和屋顶与爆炸之间的距离有关。
等效作用时间te是通过侧面上的变量计算的。
te,so = 2Iso/Pso = 2(96.0 psi·ms)/24.9 psi = 7.71 ms
后墙
修改后墙的比例距离 Z 以考虑建筑物的额外长度。 距离现在是 50 米 + 70 米，总共 120 米。 因此，Z 的计算公式如下。
再次利用来自 [2] 的图 2-15 可以确定表 2 中用于侧面压力的正的爆炸波参数。
| 爆炸荷载参数 | 由图 2-15 {% |
|
计算值 |
|---|---|---|
| Side-on 峰值压力 (+) | Pso = 4.60 psi | - |
| “侧面”冲量 (+) | Iso = 5.54W1/3 | Iso = 44.0 psi·m |
| 到达时间 | ta = 8,32W1/3 | ta = 66,0 ms |
| 指数荷载持续时间(+) | td = 3,11W1/3 | td = 24,7 ms |
| 激波前缘速度 | U = 1.5 m/m | - |
后墙等效持续时间 te可以使用上面的相关变量计算。
te,so = 2Iso/Pso = 2(44.0 psi·ms)/4.60 psi = 19.1 ms
因为后墙高出爆炸作用地面高 15 米，所以压力不是瞬时升高的。 而是使用冲击波的速度、后墙高度和到达时间来计算达到峰值压力的时间 t²。
t2 = L1/U + ta = 15.0 ft/1.26 ft/ms + 66.0 ms = 77.9 ms
爆炸荷载作用结束的时间tf现在可以被计算出来。
tf = t2 + te,so = 77,9 ms + 19,1 ms = 97,0 ms
结合上面计算得出的所有后墙面变量，建筑物这部分的压力-时间曲线是完整的。
爆炸荷载摘要
将前墙、侧墙/屋顶和后墙放在一起，可以显示总压力随时间的变化情况，并说明随着时间的推移，爆炸波如何影响结构的不同区域。
然后可以将这些信息输入到附加模块 RFEM 和附加模块 RF-DYNAM Pro-Forced Vibrations 中来定义时程曲线。
在 RFEM 中的应用
建筑物各个截面的压力-时间曲线已经定义完毕，接下来的输入数据将是 RFEM 的附加模块 RF-DYNAM Pro-强迫振动。
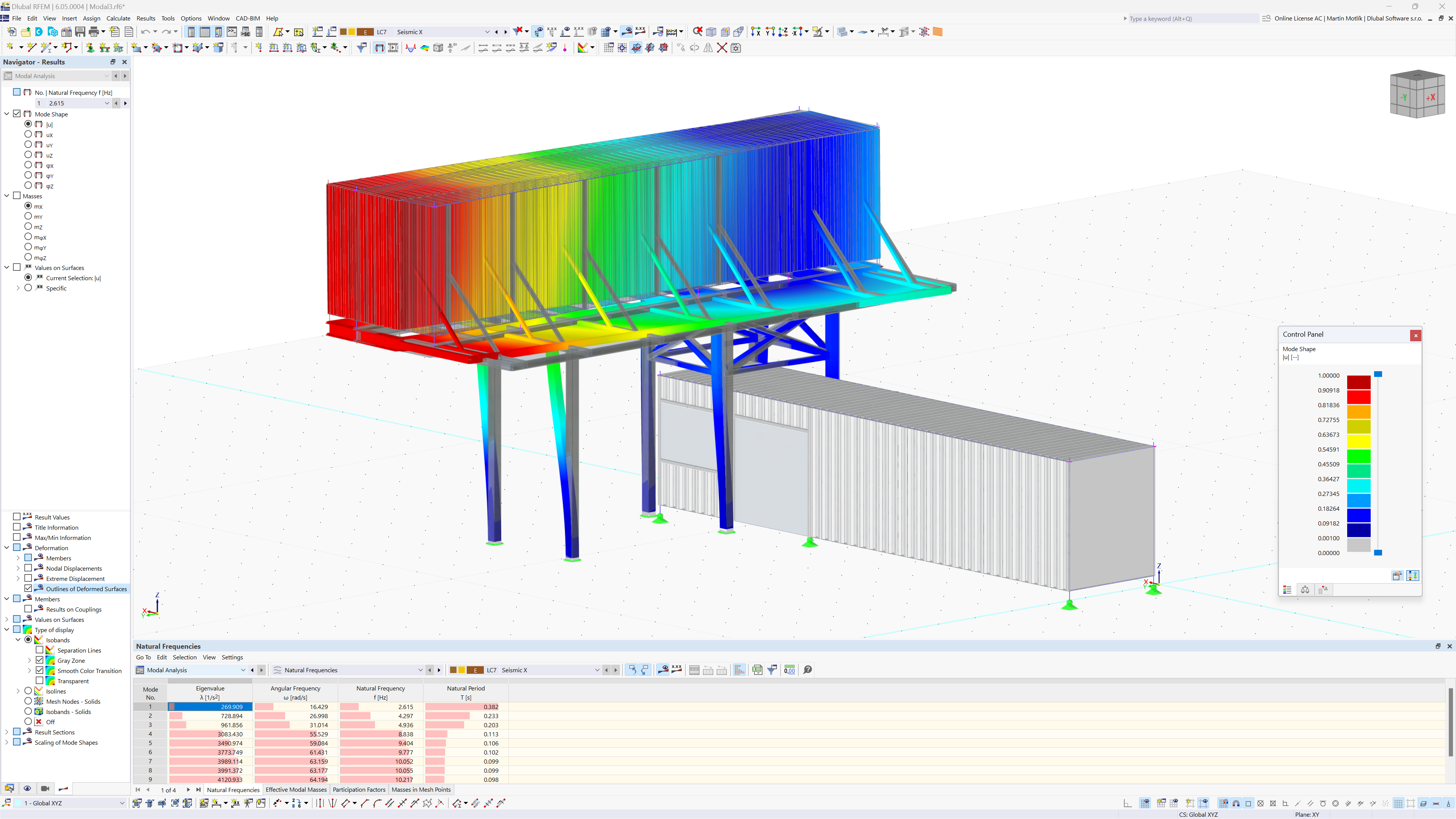
在进行时程分析之前，使用 RF-DYNAM Pro-Natural Vibrations 来确定结构的固有周期、频率和振型。 该分析部分在本文中不再详细讨论。
为了进行时程分析，为了模拟爆炸荷载在 LC1 – 前墙、LC2 – 侧墙/屋面和 LC3 – 后墙这三个荷载工况下的时程分析，在 RFEM 中被施加为三个独立的荷载工况。 这里的幅度1只是为了占位符而使用，因为该值稍后将取决于时程函数。
在 RF-DYNAM Pro-Forced Vitations 中会为结构的每个区域定义时程曲线。
请注意，每一个时程曲线都反映了上面确定的信息，例如前墙、侧墙/屋顶和后墙的峰值压力和等效持续时间。
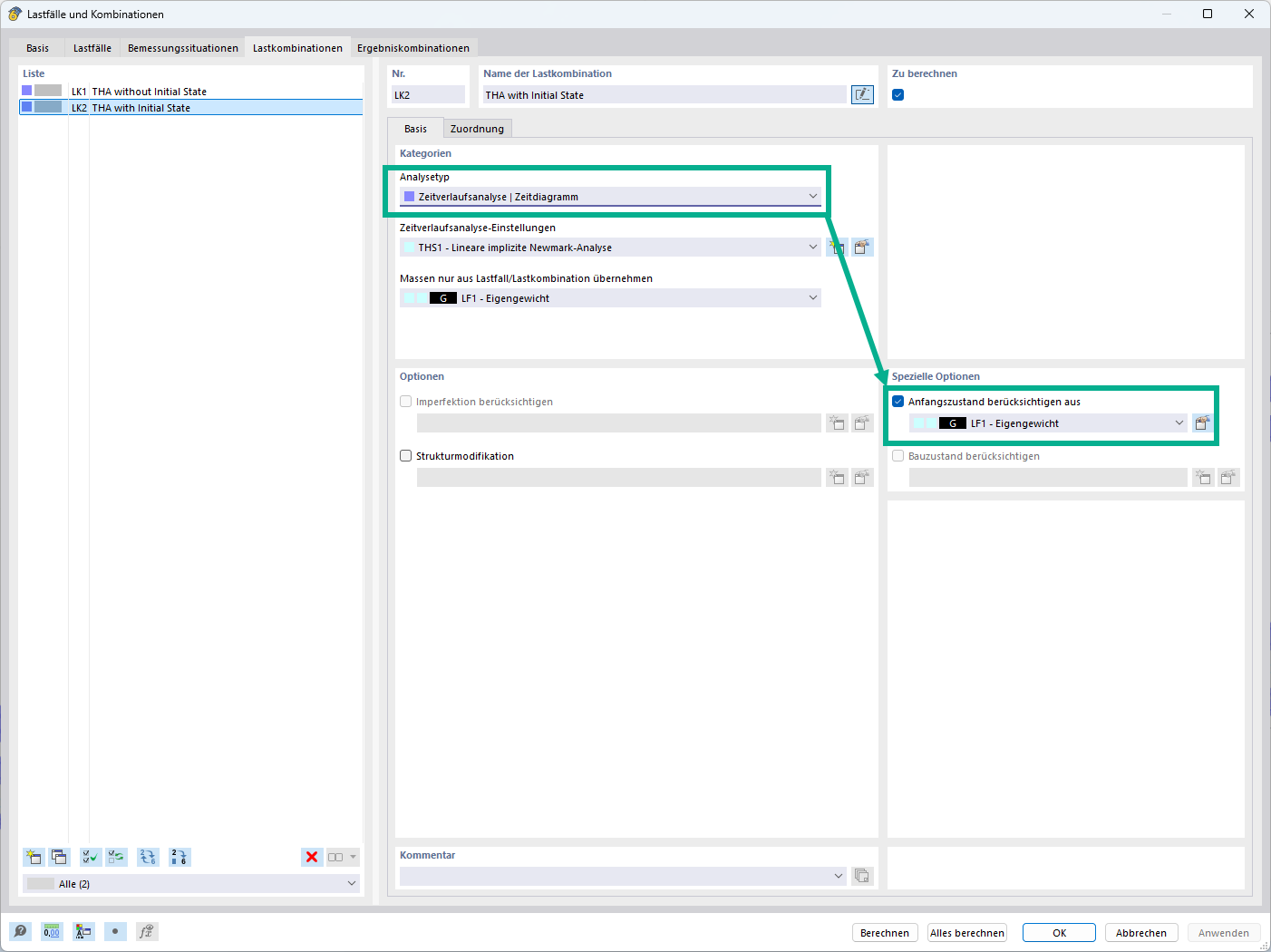
定义荷载系数时间曲线后，RFEM 中的一般面荷载将与相关图表直接链接。
在运行分析之前还必须在附加模块中设置其他变量，例如线性隐式 Newmark 分析的求解器，时程分析持续时间的最大时间为 0.5 秒，以及使用的时间步为 0.001 秒。计算中。 此外，利用固有频率分析计算得出的两个主振型的角频率，以及 2% 的 Lehr's 阻尼比，在模块中还可以设置 Rayleigh 阻尼系数 a 和 β。
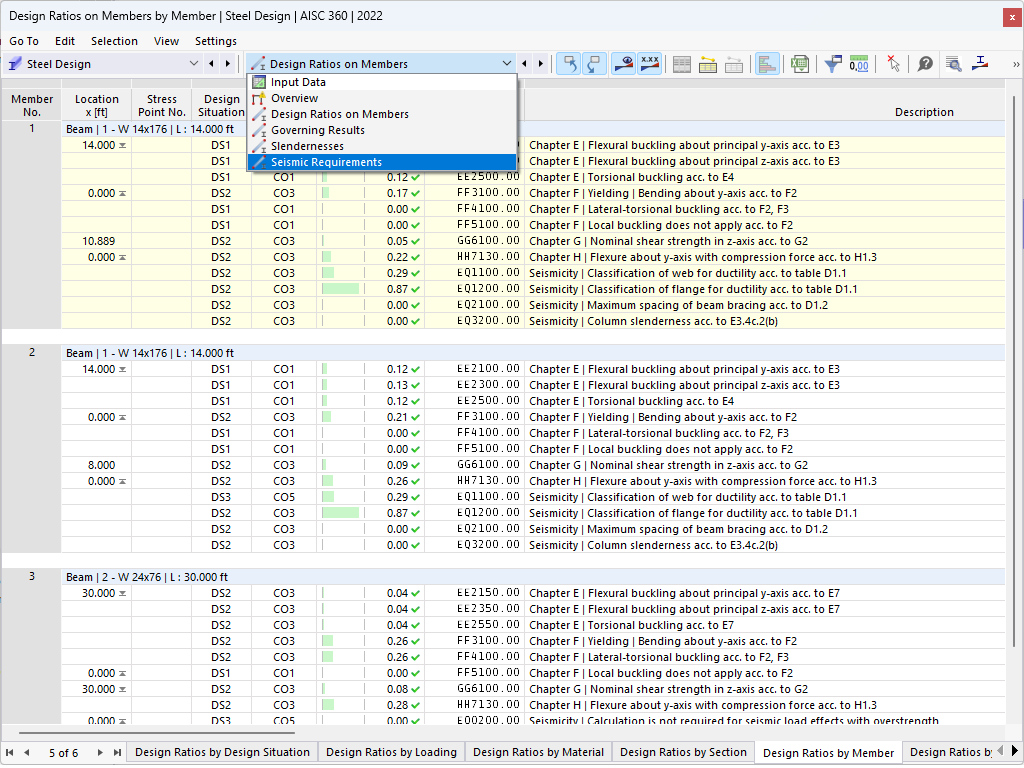
所有与爆炸时程分析相关的信息都已经定义完了，就可以在附加模块 RFEM 和 RF-DYNAM Pro 中进行计算了。 可以使用评估工具，例如 RFEM 中的时程监控器，来评估结构在爆炸爆炸过程中的响应和安全性。 有关RFEM中AISC设计向导2.1的示例2.1 {%！
