在这些货叉支座上产生扭矩,必须按照[2]章节 6.1.9 验算:
由剪力和扭矩产生的内力叠加可以避免刚性支座出现裂缝。
端部支座上的扭矩是由正弦形荷载作用下的梁挠度产生的(见图 03)。
根据[1] ,对预拱度设置值为 l/400。 这是基于加固次支承系统的最低要求。 更多相关信息例如可以在 [3] 中找到。
但是,当前的杆件分析方法无法检测支座上的扭转。 此外,许多计算程序都不允许考虑截面翘曲。 由于在二维结构杆件分析程序中经常进行计算,所以在 [2] 的 NCI 到 9.2.5.3 中提供了极限准则(表达式 2):
如果梁的长细比小于该值,则可以忽略扭转应力分量。
在 RX-TIMBER 胶合木结构中的计算
下面的例子说明了这个关系。
结构:
跨度 = 25 m
材料 = GL24c
截面 = 12 cm/242 cm (无屋脊楔形)
梁承受了 13.5 kN/m 的均匀分布荷载。 自重被忽略。
主导设计是表达式 1 中指定的扭转应力分析。 在这种情况下,lef等于跨度 2.46 m。 只有当次支承系统的水平加劲< l/500或l/1000时,才能应用用于弯扭屈曲的支座间距。 这不适用于此处。
内力和内应力:
考虑翘曲扭转的计算
RF-/FE-LTB 允许您在梁上施加偏心压力。 因此线荷载 13.5 kN/m 可以偏心施加。
如图 05 所示,荷载偏心距设为 6 cm。 此外,按照 [2] (NA.5) 施加 6.15 cm 的侧向变形。
基于伯努利弯曲理论,RF‑/FE‑LTB 可以确定临界荷载 Fki ,从而确定理想的弹性临界弯矩 Mki和扭转屈曲荷载 Nki,phi 。
计算基于二阶扭转屈曲理论。 此处还考虑了截面翘曲(第 7 自由度)。
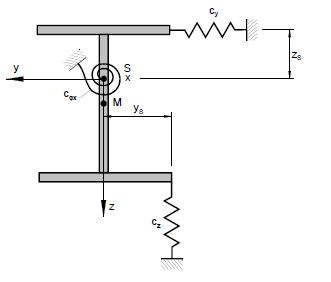
为了考虑次支承系统产生的相应屋面或加劲,定义一个绕杆件局部 x 轴转动的弹簧。 程序将此弹簧转换为剪切中心 M。
只需要一个扭力弹簧,就可以得到如图 2 所示的变形曲线。 在结构上翼缘设置一个平移弹簧会更接近于实际。 但是,由于梁的曲率,无法创建所需的缺陷形状。 然后缺陷图形从中间切开,如图 7 所示。 这样,扭矩将大大降低。
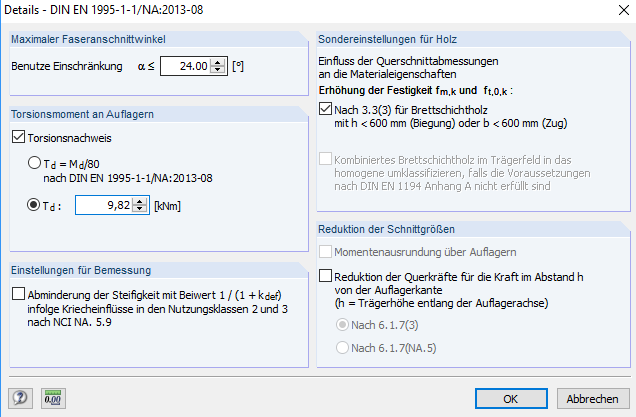
当转动约束为 500 kNm/m 时,在支座上产生的扭矩为 9.8 kNm。
利用该扭矩,在 RX-TIMBER 层板胶合木梁中可以重新进行 [1] 中的验算。 为此,在 RX-TIMBER 层板胶合木梁中定义计算的扭矩。
概述总结
通过考虑截面的翘曲刚度,可以更经济地设计结构。
与[2]中第 9.2.5 节中的一般方法的区别甚至更严重,例如在耦合杆件的纵向变形中使用 915 N/mm 的平移弹簧刚度代替.
![具有分布荷载的叉形梁(来源: [3])](/zh/webimage/009690/467522/01-de-png.png)
![胶合木梁上的裂缝(来源: [4])](/zh/webimage/009691/467524/02-de-png.png)