如果截面由多个不相连的部分截面组成,则计算惯性矩总和,不考虑平行轴定理分量。 图形01中的截面由两个不相连的角钢截面组成。
各个角钢的惯性矩如下:
Iy,1,2 = 180.39 cm4 (相对于重心轴 y、z)
Iz,1,2 = 65.05 cm4 (分别参照重心轴 y、z 轴)
整个截面的惯性矩为:
Iy,1+2 = 2 ⋅ Iy,1,2 = 2 ⋅ 180.39 = 360.78 cm4 (相对于重心 y、z 轴)
Iz,1+2 = 2 ⋅ Iz,1,2 = 2 ⋅ 65.05 = 130.11 cm4 (相对于重心轴 y、z)
如果截面由多个相连的部分截面组成,则计算惯性矩总和时使用平行轴部分定理。 图 02 中所示的截面由两个角钢截面相连。
角钢的截面属性如下:
A1.2 = 16.25 厘米²
yS,0,1,2 = ±2,30 cm(相对于零点)
zS,0,1,2 = 3.07 cm(相对于零点)
Iy,1,2 = 180.39 cm4 (相对于重心轴 y、z)
Iz,1,2 = 65.05 cm4 (分别参照重心轴 y、z 轴)
计算整个截面的截面属性:
yS,0,1+2 = 0.00 cm(相对于零点)
zS,0,1+2 = 3,07 cm(相对于零点)
Iy,1+2 = 2 ⋅ Iy,1,2 + 2 ⋅ A1,2 ⋅ (zS,0,1,2 - zS,0,1+2 )²
Iy,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 - 3,07)² = 360,78 cm4 (相对于重心 y、z 轴)
Iz,1+2 = 2 ⋅ Iz,1,2 + 2 ⋅ A1,2 ⋅ (yS,0,1,2 - yS,0,1+2 )²
Iz,1+2 = 2 ⋅ 65.05 + 2 ⋅ 16.25 ⋅ (2.30 - 0.00)² = 301.46 cm4 (相对于重心 y、z 轴)








..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)












.png?mw=350&hash=154cfb9bf427390b9a61c822d106bf243d0c64e8)













![膜结构的基本形状[1]](/zh/webimage/009595/2419509/01-png.png?mw=512&hash=fe42d914122820fe3c92f9595d4d91afce8a2c07)


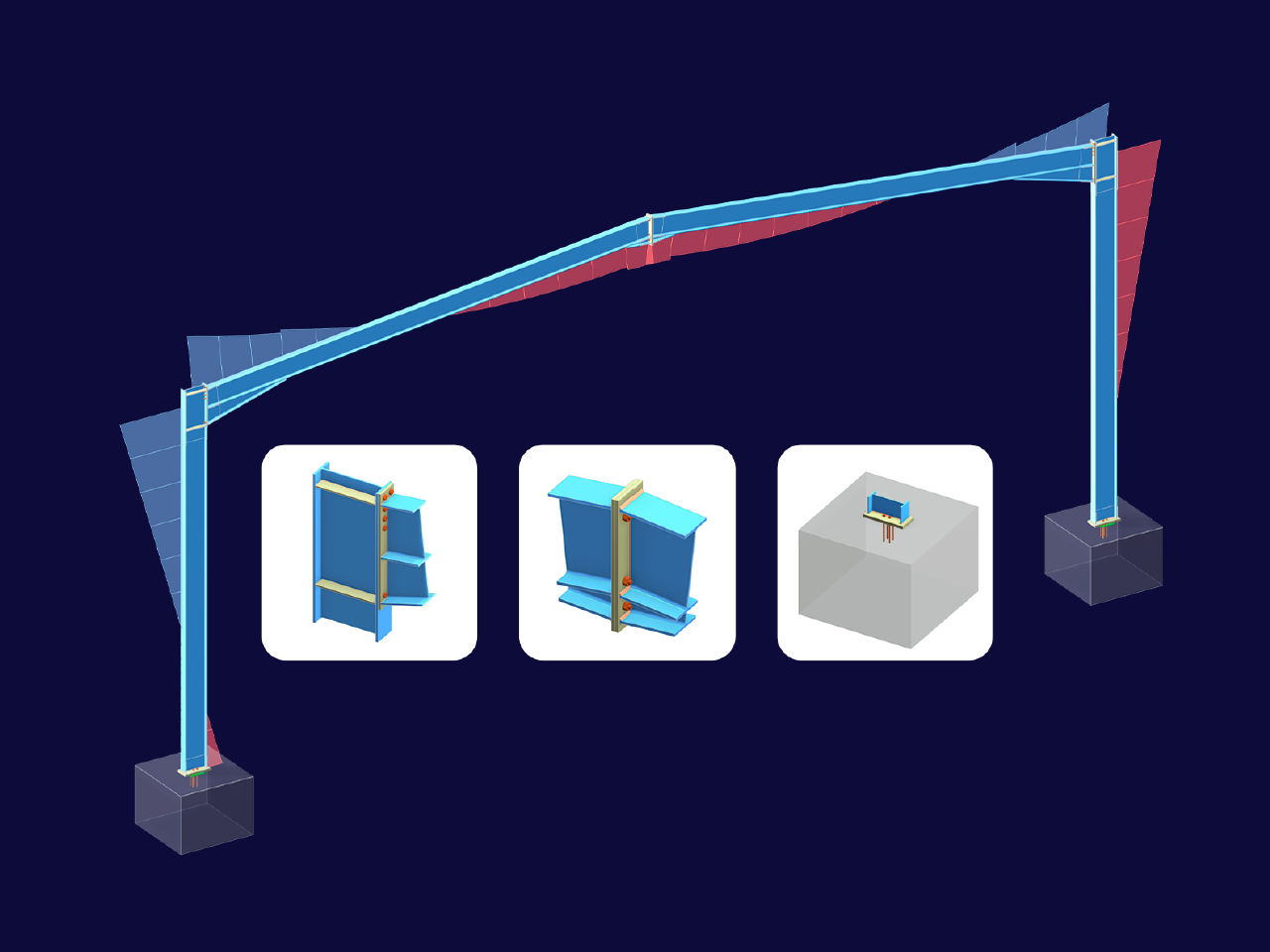
















_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)