Modelado de la interacción suelo-estructura

Hay varios principios disponibles para simular la interacción suelo-estructura. Este capítulo describe los diferentes enfoques de modelado en orden ascendente de detalle. Es importante tener en cuenta que el tiempo de modelado y cálculo generalmente aumenta debido a una simulación más detallada de la interacción suelo-estructura con una mayor precisión. La figura siguiente muestra los distintos métodos.

Representación esquemática de diferentes modelos de suelo para la interacción suelo-estructura

2D | Método del coeficiente de balasto

En la simulación bidimensional de un suelo, se disponen muelles equivalentes en el área de la base de la cimentación.

En el método del módulo de reacción de la subrasante (también cimentación de Winkler), la rigidez de estos muelles se describe como constante debido a la relación lineal entre la tensión de contacto del suelo y el asiento resultante.

Aquí, se omiten la rigidez a cortante y el suelo adyacente, lo que da como resultado una zanja de hundimiento en lugar de un depósito de hundimiento. Este comportamiento de interacción es más realista para arena seca homogénea, donde la rigidez a cortante es muy baja.
Para considerar la rigidez a cortante y el suelo adyacente, y para representar un comportamiento de asiento más realista, se han desarrollado diferentes modificaciones de este método.

2D | Método del coeficiente de balasto modificado (módulo modificado de reacción de la subrasante)

Las modificaciones más simples aumentan la rigidez elástica en el área del borde de una manera simplificada para simular la rigidez creando un depósito de hundimiento. La siguiente figura muestra el método según Dörken und Deehne [1] a la izquierda, donde el área de una cuarta parte de la dimensión de la cimentación se incrementa linealmente hasta el doble de la rigidez. Por el contrario, muestra el aumento del módulo de asiento según Bellmann y Katz [2], mientras que en la fila exterior de elementos finitos, se aplica la rigidez, aumentada por un factor de 4.

Método del módulo de reacción modificado

Tipo 2D | Método modificado del módulo de reacción de la subrasante de dos parámetros con solapamiento de cimentación

Para considerar la resistencia a cortante y las áreas de suelo adyacentes de forma más realista, el modelo de suelo se modifica aplicando un solapamiento de cimentación sin rigidez relevante. Esto debería ser suficiente para que el asiento en su borde sea insignificante. La ventaja aquí es que puede considerar las cimentaciones adyacentes además de la resistencia a cortante.
El cálculo del módulo de reacción de la subrasante c_1,z en la dirección vertical, así como la resistencia a cortante c_2,v, se puede realizar según los dos métodos siguientes según Pasternak o Barwaschow [3].

Tipo 2D | Método modificado del módulo de reacción de la subrasante de dos parámetros con muelles equivalentes

Según Kolar y Nemec [5], es posible utilizar el método del suelo eficaz para simular una cuenca de hundimiento mediante la disposición de muelles adicionales. Estos muelles adicionales se aplican a los contornos y puntos de esquina de la cimentación. Se puede determinar según las siguientes fórmulas.

2D | Método del módulo limitado (espacio medio elástico)

Es posible una simulación aún más precisa del modelo de suelo utilizando el método del módulo de rigidez (semiespacio elástico) [6]. Al determinar las posibles capas del suelo, la cuenca de hundimiento y realizar el cálculo iterativo de la interacción suelo-estructura, este método le permite calcular las distribuciones de los coeficientes de cimentación elástica cercanos a la realidad.

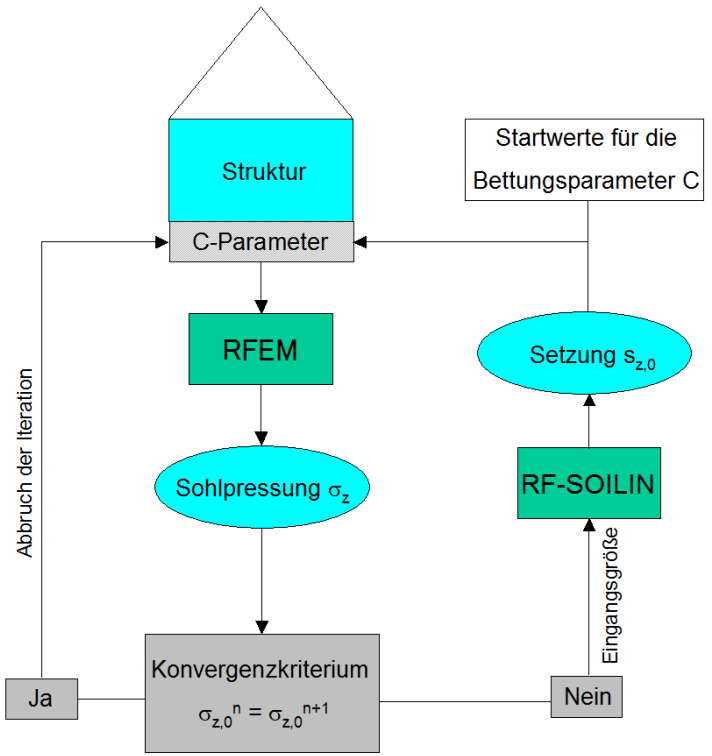
La distribución de los parámetros de la cimentación bajo la losa de cimentación es necesaria para el cálculo de las tensiones de contacto del suelo. Al mismo tiempo, depende de estas compresiones. Debido a la compleja interacción entre el suelo y la estructura, es imposible determinar los parámetros de la cimentación en un cálculo simple. El primer paso de iteración requiere que se seleccionen los valores iniciales para los parámetros de la cimentación. Estos valores iniciales se pueden usar para realizar un análisis de elementos finitos del modelo. El resultado es la distribución de las tensiones de contacto del suelo.
Las tensiones de contacto del suelo del primer paso de iteración se incluyen como valores iniciales para otro cálculo. Junto con los módulos de rigidez de las capas de suelo introducidas, es posible calcular el asiento para cada elemento finito. El asiento y la tensión de contacto del suelo se utilizan para calcular los parámetros de la cimentación. En el siguiente paso de iteración, los nuevos parámetros de la cimentación reemplazan a los antiguos y se inicia un nuevo análisis por elementos finitos, que a su vez
proporciona una nueva distribución de tensiones de contacto con el suelo. Como criterio de convergencia, la nueva distribución de tensiones se compara con la anterior. Siempre que la desviación no caiga por debajo de un cierto límite de convergencia, la nueva distribución de tensiones se incluye en el cálculo de los nuevos parámetros de la cimentación.
Si no se alcanza la diferencia de la distribución de tensiones de contacto del suelo de dos pasos de iteración sucesivos, se finaliza la iteración. Como resultado, se muestran los parámetros de la cimentación del último paso de iteración. La siguiente figura muestra el proceso de cálculo esquemático utilizando el método del módulo de rigidez (semiespacio elástico).

Cálculo iterativo de los parámetros de la subestructura en semiespacio elástico

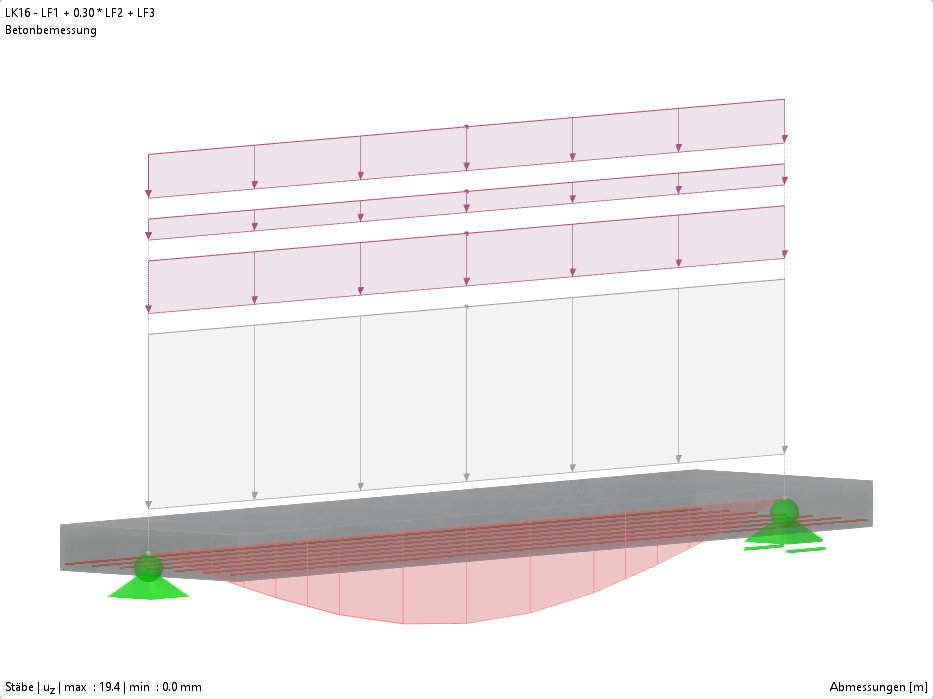
Un valor intermedio importante en el cálculo iterativo de los parámetros de la cimentación son los asientos s_z. Para la distribución de tensiones debidas a la sobrecarga, el suelo se considera como un semiespacio homogéneo con material isótropo elástico lineal según el modelo de Boussinesq. Esto se muestra en la siguiente figura. Aquí, los componentes del asiento se consideran hasta una profundidad límite, que resulta o bien de un incremento de tensión insignificante debido a la sobrecarga en comparación con la tensión del peso propio del suelo, o de la aplicación de una capa incompresible (p. ej. roca maciza). La tensión se integra por capas. Los asientos se calculan junto con el módulo de rigidez correspondiente. Con la tensión de contacto del suelo 𝜎_z y los asientos s_z, se calculan los parámetros de la cimentación.

Distribución de tensiones en semiespacio elástico

3D

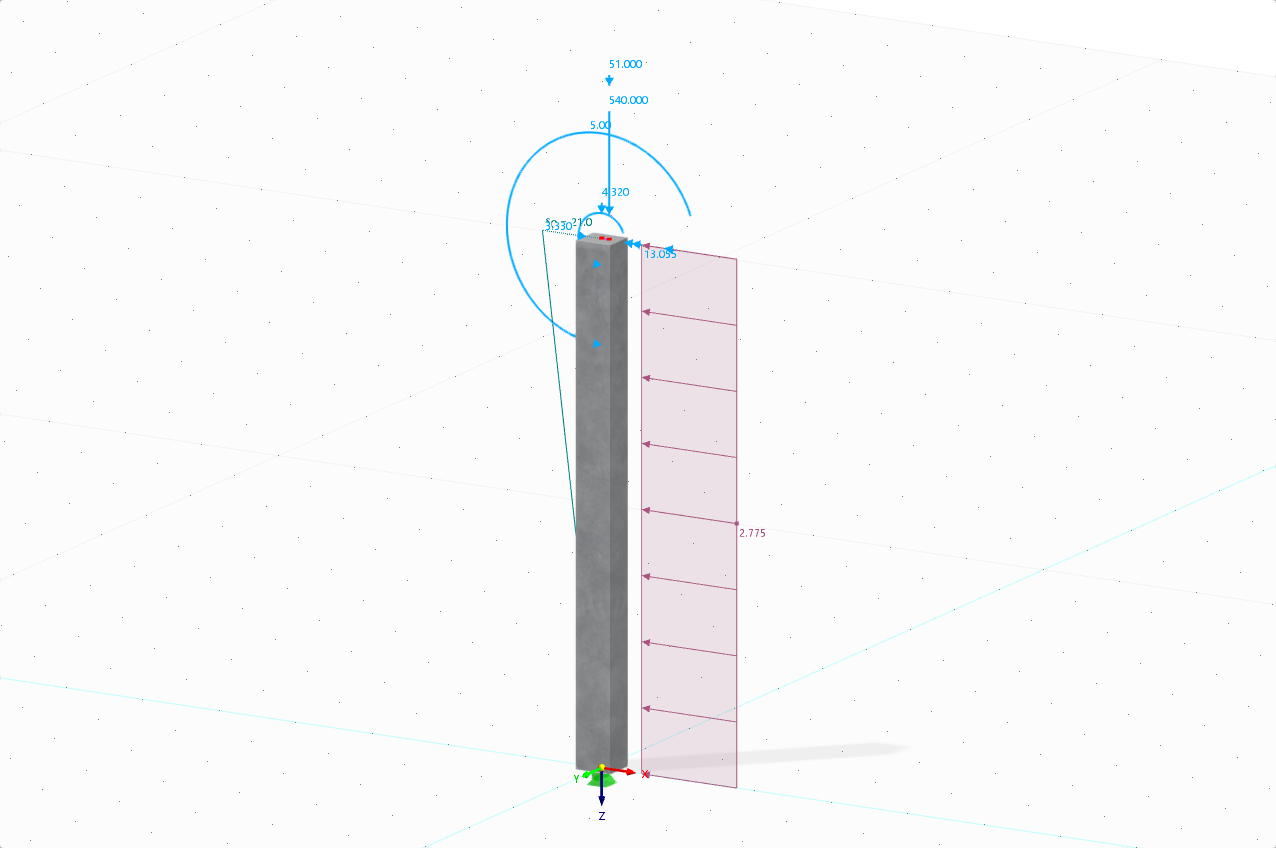
La simulación más realista y compleja de la interacción suelo-estructura es posible utilizando la deformación de las condiciones del suelo existentes en un análisis de EF en 3D. Aquí se puede considerar cualquier condición geométrica y del material. El comportamiento estructural del suelo se puede modelar, por ejemplo, por medio de modelos de materiales especiales de acuerdo con la realidad. La interacción de las cimentaciones adyacentes se determina mediante su relación geométrica mediante el mallado tridimensional y la compatibilidad.