Modélisation de l’interaction sol-structure

Différentes théories sont disponibles pour la simulation de l’interaction sol-structure.
Ce chapitre décrit les différentes approches de modélisation avec un niveau de détail croissant. Gardez à l’esprit qu’une simulation plus détaillée de l’interaction sol-structure entraîne souvent une augmentation de son exactitude, d’une part, et de la complexité de la modélisation et des calculs, d’autre part. L’image suivante montre schématiquement les différentes méthodes.

Représentation schématique de plusieurs modèles de sol pour l’interaction sol-structure

2D | Méthode du module de réaction

Dans la modélisation bidimensionnelle du sol, des ressorts équivalents sont placés sur la surface inférieure des fondations.

Dans la méthode du module de réaction (également dite de Winkler), la rigidité de ces ressorts est décrite comme constante en raison de la relation linéaire entre la pression de contact et le tassement résultant.

Ici, la rigidité au cisaillement et le sol adjacent sont négligés, ce qui crée un sillon de tassement au lieu d'une cuvette de tassement. Ce comportement d'interaction est plus réaliste pour du sable homogène sec, car sa rigidité au cisaillement est très faible. Différentes modifications de cette méthode ont été développées pour inclure la rigidité au cisaillement et le sol adjacent et représenter un comportement plus réaliste du tassement.

2D | Méthode du module de réaction modifiée

Les modifications les plus simples augmentent simplement la rigidité des ressorts aux bords pour simuler la rigidification due à la formation d’une cuvette de tassement. L’image ci-dessous montre sur son côté gauche la méthode selon Dörken et Dehne [1], où une zone d’un quart de la dimension de la fondation est augmentée linéairement à une rigidité doublée. En comparaison, l’augmentation du module de réaction selon Bellmann et Katz [2] est présentée, dans la rangée externe d'éléments finis, une rigidité augmentée d’un facteur 4 est appliquée.

Méthode de module de réaction du sol modifié

2D | Méthode modifiée du module de réaction à deux paramètres avec dépassement de fondation

Pour une prise en compte plus réaliste de la capacité de cisaillement et des zones de sol adjacentes, la modification du modèle de sol utilise l'approche d'un dépassement de fondation sans rigidité significative. Celui-ci doit s'étendre suffisamment pour que les tassements à son bord puissent être négligés. L’avantage ici est que, outre la capacité de cisaillement, il est également possible de prendre en compte des fondations adjacentes. Le calcul du module de réaction c_1,z dans la direction verticale ainsi que de la capacité de cisaillement c_2,v peut être effectué selon les deux méthodes suivantes de Pasternak ou Barwaschow [3].

2D | Méthode du module de réaction modifiée à deux paramètres avec ressorts équivalents

Selon Kolar et Nemec [5], une simulation de la cuvette de tassement peut être effectuée à travers la méthode du sol effectif par la disposition de ressorts supplémentaires. Ces ressorts supplémentaires sont appliqués aux lignes extérieures et aux points d'angle de la fondation. L'évaluation peut être effectuée selon les formules suivantes.

2D | Méthode du module de rigidité (demi-espace élastique)

Une simulation encore plus précise du modèle de sol est possible via la méthode du module de rigidité (demi-espace élastique) [6]. Grâce à l'intégration des éventuelles stratifications du sol, de la cuvette de tassement et du calcul itératif de l’interaction sol-structure, cette méthode permet de calculer des distributions proches de la réalité des coefficients de fondation élastiques.

La distribution des paramètres de fondation sous la semelle de fondation est requise pour le calcul des pressions de semelle. En même temps, elle en dépend. En raison de l’interaction complexe entre le sol et la structure, déterminer les paramètres de fondation en un simple passage de calcul est impossible. Pour la première étape d’itération, des valeurs initiales doivent être sélectionnées pour les paramètres de fondation. Avec ces valeurs de départ, une analyse par éléments finis du modèle peut être réalisée. Le résultat est la distribution des pressions de contact.

Les pressions de contact de la première étape d'itération sont ensuite utilisées comme entrée pour un nouveau calcul. Avec les modules de rigidité des couches de sol entrées, le tassement peut être calculé pour chaque élément fini. À partir du tassement et de la pression de contact, les paramètres de fondation sont calculés. Dans la prochaine étape d’itération, les nouveaux paramètres de fondation remplacent les anciens et une nouvelle analyse par éléments finis est effectuée, qui produit à son tour une nouvelle distribution des pressions de contact. Comme critères de convergence, les nouvelles distributions des pressions de contact et des tassements sur la surface de la fondation sont comparées aux anciennes.

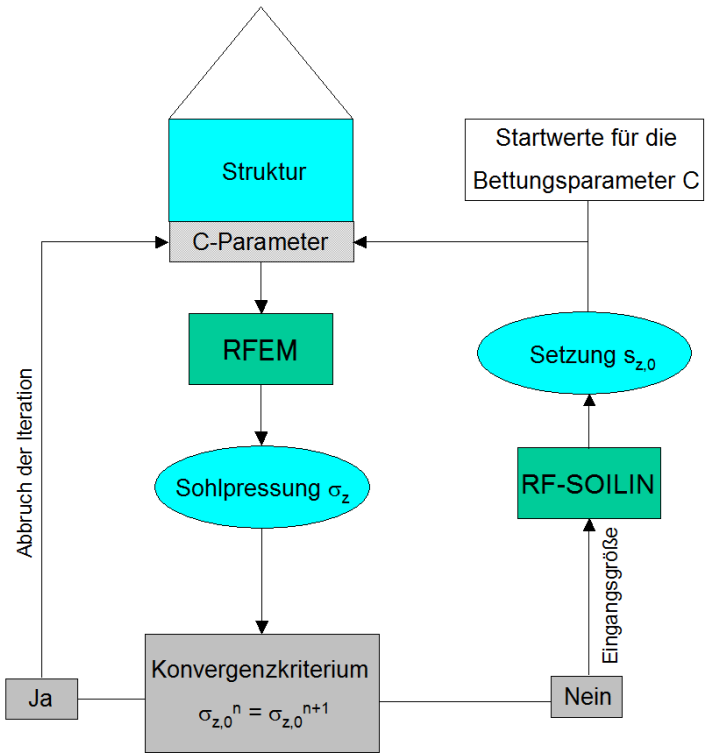
Tant que la déviation ne tombe pas en dessous d’un seuil de convergence prédéfini et que le nombre maximal d’itérations n’est pas atteint, le calcul itératif se poursuit. Si les seuils de convergence de deux étapes d’itération consécutives sont franchis, l’itération est terminée. Le résultat final est les paramètres de fondation de la dernière étape d’itération. L’image suivante montre le processus de calcul schématique utilisant la méthode du module de rigidité (demi-espace élastique).

Calcul itératif des paramètres de réaction dans le demi-espace élastique

Une grandeur intermédiaire cruciale dans le calcul itératif des paramètres de fondation sont les tassements s_z. Pour la distribution des contraintes due à la charge, le sol est considéré comme un demi-espace homogène avec un matériau linéairement élastique et isotrope selon le modèle de Boussinesq, comme le montre l’image suivante. Ici, les contributions de tassement sont prises en compte jusqu’à une profondeur limite, déterminée soit par une augmentation négligeable de la contrainte due à la charge comparée à la contrainte du poids propre du sol, soit sur la base d'une couche incompressible (par exemple, roche dure). Les contraintes sont intégrées couche par couche. Avec le module de rigidité correspondant, les tassements sont calculés. Avec la pression de base 𝜎_z et les tassements s_z, les paramètres de fondation sont calculés.

Distribution des contraintes dans un demi-espace élastique

Pour obtenir indirectement une augmentation de la rigidité avec la profondeur, on peut réduire la tension de la charge par la tension initiale factorisée (due au poids propre du sol). Cela peut éventuellement conduire à un comportement physiquement plus raisonnable. Pour le calcul des tassements, seules les surtensions résultantes sont prises en compte.

Affichage des contraintes efficaces/réductrices

Les paramètres de fondation de cette méthode sont dérivés de l'égalité de l'énergie potentielle entre le modèle 3D et le modèle 2D. Une description complète est incluse dans la thèse [7]. Ici, outre la relation contrainte-déformation verticale, la rigidité au cisaillement en zx et yz est également intégrée. Il est important de noter que cela correspond à une matrice de compliance réduite à la diagonale (E_z et G) et que pour transférer le problème de 3D à 2D, l’intégration le long de l’axe z est effectuée. Cela entraîne les relations suivantes pour déterminer les paramètres de fondation pour la déformation verticale (C_u,z) et la déformation en cisaillement (C_v,xz et C_v,yz). Ces derniers ne sont pas calculés directement à partir de la déformation pour éviter des problèmes numériques, mais sont exprimés sous la forme dite isotrope. En raison de l’influence mutuelle de ces paramètres de fondation et de la pression de contact, il en résulte également la nécessité de la détermination itérative mentionnée initialement de l’interaction sol-structure.

De plus, pour représenter l'effet raideur du bassin de tassement, les fondations linéaires (C_l,u,z) dérivés de ces paramètres de fondation sont appliqués sur les lignes de bord. Cependant, il est fortement recommandé de prévoir un dépassement de fondation qui s'étend au moins jusqu'à ce que les tassements soient complètement dissipés à son bord extérieur.

3D

La simulation la plus réaliste mais aussi la plus complexe de l'interaction sol-structure est possible par la modélisation des états présents dans une analyse 3D par éléments finis. L'interaction des fondations adjacentes est considérée à travers leur relation géométrique par maillage tridimensionnel et compatibilité. Ici, les conditions géométriques et matérielles peuvent être prises en compte de manière réaliste. Le comportement porteur du sol peut par exemple être modélisé de manière réaliste à l'aide de modèles de matériaux spéciaux non linéaires. Il est important ici de prendre en compte l'état initial, car la plupart des modèles de matériaux non linéaires dépendent de l'état de contrainte tridimensionnel. Cela peut être illustré par la surface de rupture du modèle de Mohr-Coulomb modifié. Si on s'éloigne du point d'origine sur l'axe hydrostatique sous pression uniforme, les changements de contrainte tolérables avant d'atteindre le critère de plasticité sont plus importants.