考虑弹性柔度的木结构连接

• 3D Viewer | Google
• 3D Viewer | Babylon
• 虚拟现实

木结构连接的灵活性

极惯性矩

如图01所示，连接的极惯性矩为：

I_p = 75 ² + 75 ² + 225 ² +225 ² = 112,500 mm ²

正常使用极限状态下的位移模量

在正常使用极限状态下的位移模量可以根据[1]表7.1计算。 对于软木C24中径为20 mm的螺栓，得出的每个剪切平面如下：

_ķSER = 420 ^1.5⋅20/23 = 7485牛顿/毫米= 7485千牛/米

由此得出一个内部钢板的两个剪力面。 此外，对于钢板-木结构连接，按照[1]中第7.1（3）章的规定，位移模量应乘以系数2.0。 您可以按照下列方法确定螺栓的位移模量：

K_ser = 2⋅2⋅7,485 kN/m = 29,940 kN/m

极限承载力状态下的位移模量

根据[1] ，处于极限状态的连接位移模量K_u ：

K_u = 2/3⋅29,940 kN/m = 19,990 kN/m

[2]和[3]需要考虑连接的位移模量的设计值。

K_d = 19,960 kN/m/1.3 = 15,354 kN/m

确定扭转弹簧刚度

对于承载能力极限状态设计，必须使用滑模模量的设计值和正常使用极限状态设计的平均值，因此得出两个扭转弹簧刚度。

_Cφ，SLS = 29,940 N/mm⋅112,500 mm ² = 3,368 kNm/rad

_Cφ，ULS = 15,354 N/mm⋅112,500 mm ² = 1,727 kNm/rad

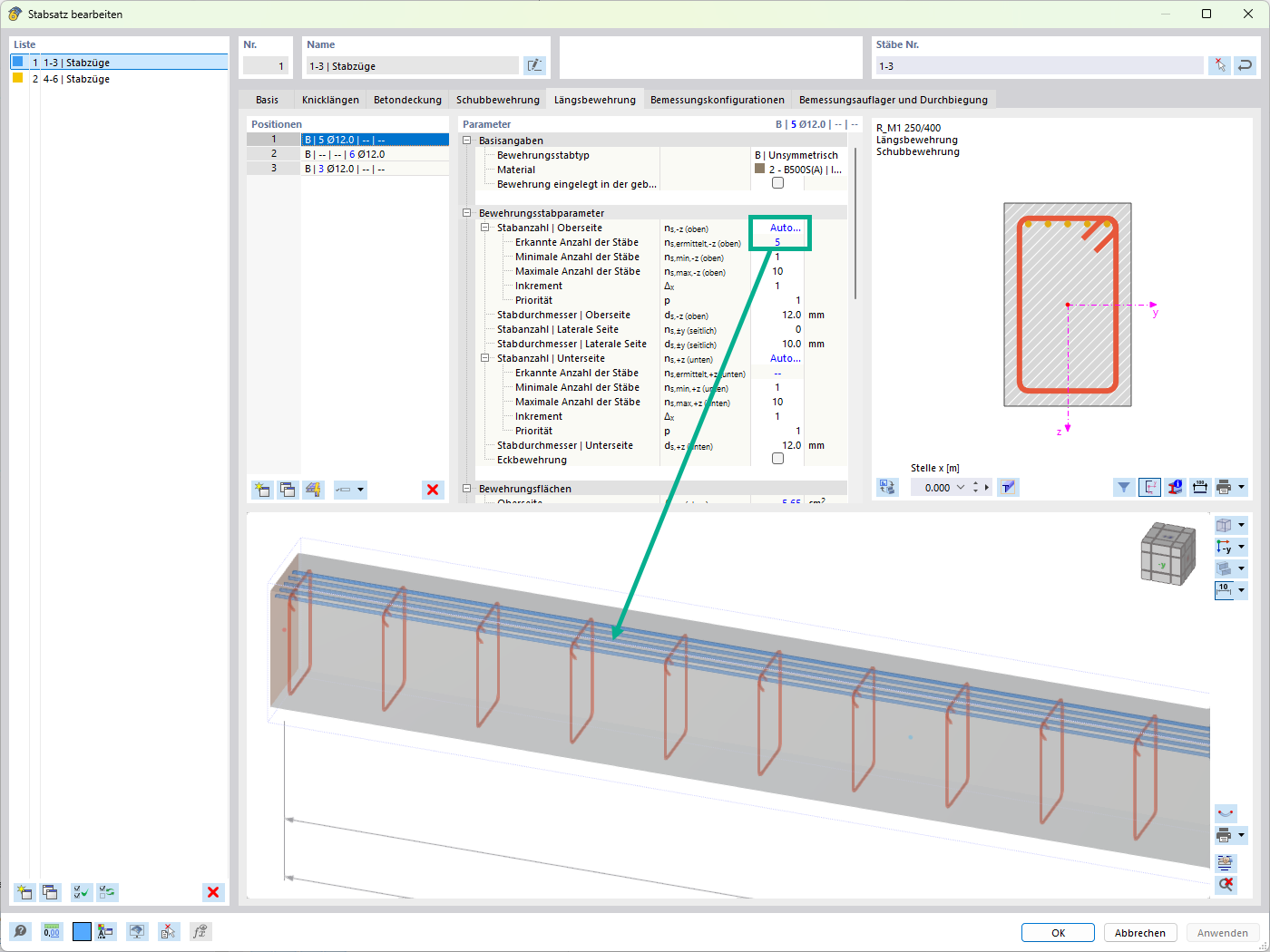
要同时考虑两种刚度，请激活“修改刚度”子选项卡（在“编辑荷载组合和计算”对话框中的荷载组合的计算参数子选项卡中勾选相应的复选框）。 因此，正如在本例中一样，所有 ULS 组合的抗扭刚度都可以乘以系数 C_{φ, ULS}/C_{φ, SLS} 。 _{输入Cφ，SLS}在支座或铰接条件。 因此，在所有ULS组合中得出的扭转弹簧刚度为1.727 kNm/rad，在所有SLS组合中得出时的值为3.368 kNm/rad。 在视频中也介绍了这种方法。

在本示例中，基础弹性旋转是无限大的，并且没有考虑。

附加模块 RF-/JOINTS Timber - Steel 确定抗扭弹簧刚度

当使用RF-/JOINTS Timber -Steel to Timber计算连接时，也会显示扭转弹簧刚度结果（见图02）。 在RSTAB中必须在支座或铰接条件下手动转移。 在RFEM中可以自动完成。 各连接节点在RFEM中自动创建，并采用相应的刚度。 该视频显示了该操作步骤。

• 3D Viewer | Google
• 3D Viewer | Babylon
• 虚拟现实

RF-/JOINTS Timber -Steel to Timber：转动弹簧刚度