7125x

2018-09-12

Pannelli irrigiditi secondo EN 1993-1-5, punto 4.5

In SHAPE-THIN, il calcolo dei pannelli irrigiditi può essere eseguito secondo la sezione 4.5 della EN 1993-1-5. Per i pannelli irrigiditi, devono essere considerate le superfici efficaci dovute all'instabilità locale dei singoli pannelli nella piastra e negli irrigidimenti, nonché le superfici efficaci dall'instabilità dell'intero pannello dell'intero pannello irrigidito.

Prima di tutto, le superfici efficaci dei singoli pannelli sono determinate utilizzando il coefficiente di riduzione secondo EN 1993-1-5 [1] , Sezione 4.4 per tenere conto dell'instabilità dei singoli pannelli. Nella seconda fase, la sicurezza all'instabilità dell'intero pannello è determinata tenendo conto del comportamento all'instabilità simile a quello di una delle aste instabili. Con il coefficiente di riduzione dell'instabilità globale del pannello, le larghezze efficaci dei singoli pannelli si riducono. Ciò si traduce in una sezione trasversale efficace che può essere gestita come appartenente alla classe di sezione trasversale 3.

Esempio

Il seguente esempio è tratto dall'Annuario delle strutture in acciaio 2015 [2]. La sezione trasversale è costituita da una trave a I di cui l'anima è irrigidita da irrigidimenti trasversali rigidi e da un irrigidimento longitudinale. Gli irrigidimenti trasversali sono disposti ad una distanza di 3.000 mm l'uno dall'altro e l'irrigidimento longitudinale è saldato ad una distanza di 500 mm dall'ala inferiore. Si trascurano le saldature. Una forza assiale di compressione di N_Ed = 4.000 kN agisce.

Sezione trasversale

Materiale:
S355 J0
f_y = 35,5 kN/cm² (per t ≤ 3 mm e t ≤ 16 mm)
f_y = 34,5 kN/cm² (per t >16 mm e t ≤ 40 mm)
E = 21.000 kN/cm²
G = 8.076,92 kN/cm²
γ_M0 = 1.0

a = 3.000 mm
b₁ = 500 mm
b₂ = 2.500 mm
_bf = 800 mm
b_st = 250 mm
t_w = 15 mm
_tf = 40 mm
t_st = 25 mm
h = 3.080 mm

Sezione trasversale lorda e distribuzione delle tensioni

Le tensioni sono calcolate come segue:

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4.000}{1.152, 5} = 3, 47 kN / cm ²

Formula 1

La sezione trasversale lorda è la distribuzione delle tensioni sono mostrate in figura 02.

distribuzioni delle tensioni

Classificazione della sezione

Durante una classificazione della sezione trasversale, viene eseguita una valutazione per accertare se è necessario un progetto di instabilità per i singoli pannelli. Se il singolo pannello è almeno di classe 3, l'instabilità locale non è determinante.

corrente

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392, 5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392, 5}{40} = 9, 8 \end{array}

Formula 2

Il rapporto c/t massimo λ_i è determinato secondo EN 1993-1-1 [3] , Tabella 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{c_{f}}{t_{f}} = 9, 8 \end{array}

Formula 3

La flangia deve essere assegnata alla classe 3 L'instabilità locale quindi non è determinante e non è necessaria alcuna riduzione dei singoli pannelli dell'ala.

anima

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487, 5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487, 5}{15} = 32, 5 \end{array}

Formula 4

Il rapporto c/t massimo λ_i è determinato secondo [3] , Tabella 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 > \frac{c_{1}}{t_{w}} = 32, 5 \end{array}

Formula 5

Il singolo pannello 1 deve essere assegnato alla classe 3. L'instabilità locale quindi non è determinante e non è necessaria alcuna riduzione dei singoli pannelli dell'ala.

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2.500 - \frac{25}{2} = 2.487, 5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2.487, 5}{15} = 165, 8 \end{array}

Formula 6

Il rapporto c/t massimo λ_i è determinato secondo [3] , Tabella 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 < \frac{c_{2}}{t_{w}} = 165, 8 \end{array}

Formula 7

Il singolo pannello 2 deve essere assegnato alla classe 4. L'instabilità locale determina quindi per questo singolo pannello ed è necessaria una riduzione di questo singolo pannello.

Rinforzo

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

Formula 8

Il rapporto c/t massimo λ_i è determinato secondo [3] , Tabella 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

Formula 9

L'anima deve essere assegnata alla classe 3. L'instabilità locale quindi non è determinante e non è necessaria alcuna riduzione di questo singolo pannello.

Larghezze efficaci

Il singolo pannello 1 è assegnato alla classe di sezione trasversale 3 in modo che l'instabilità locale non sia determinante. I valori della sezione trasversale efficace corrispondono ai valori della sezione trasversale lorda. Secondo [1] , Tabella 4.1, ciò risulta nelle seguenti larghezze efficaci:

\begin{array}{l} b_{1, eff} = c_{1} = 487, 5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \end{array}

Formula 10

Il singolo pannello 2 è assegnato alla classe di sezione trasversale 4 in modo che l'instabilità locale non sia determinante. Le larghezze efficaci del singolo pannello 2 devono essere determinate secondo [1] , Sezione 4.4.

La distribuzione delle tensioni nel singolo pannello 2 è uniforme. Ciò si traduce in un rapporto di tensione di ψ = 1 e, secondo la Tabella 4.1, in un valore di instabilità di k_σ = 4.0. Per il rapporto di snellezza λ_p2, il risultato è, secondo [1] , Sezione 4.4(2):

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165, 8}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 3, 588$ Formula 12	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Formula 13
	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Formula 14

Il coefficiente di riduzione locale ρ è determinato secondo [1] , equazione (4.2):

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0, 055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3, 588 - 0, 055 \cdot (3 1)}{3, 588^{2}} = 0, 262 < 1

Formula 15

Le larghezze efficaci del singolo pannello 2, tenendo conto dell'instabilità locale, sono calcolate secondo [1] , Tabella 4.1:

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0, 262 \cdot 2.487, 5 = 650, 7 mm \\ b_{2, edge, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \\ b_{2, \sup, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \end{array}

Formula 16

Le larghezze della sezione trasversale lorda risultano:

\begin{array}{l} b_{2, edge} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \\ b_{2, \sup} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \end{array}

Formula 17

Comportamento delle piastre

La tensione critica elastica della rigidezza σcr,sl è calcolata secondo [1] , Appendice A.2.2. La lunghezza efficace della rigidezza a_c deve essere calcolata prima:

a_{c} = 4, 33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4, 33 \cdot \sqrt[4]{\frac{11.900 \cdot 50^{2} \cdot 250^{2}}{1, 5^{3} \cdot (50 250)}} = 896, 4 cm > a = 300 cm

Formula 18

La tensione critica elastica della rigidezza σ_cr,sl risulta in a < a_c in:

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

Formula 19

I_sl,1 e A_sl,1 rappresentano qui il secondo momento dell'area della sezione trasversale lorda e l'area della sezione trasversale lorda dell'asta equivalente compressa secondo [1] ; A.2.1(2) per instabilità perpendicolare al piano della piastra e b₁ e b₂ descrivono le distanze degli irrigidimenti dai bordi longitudinali (b₁ + b₂ = b).

La distribuzione delle tensioni è uniforme. Pertanto, la tensione di instabilità della piastra elastica σ_cr,p corrisponde alla tensione di instabilità critica σ_cr,sl.

σ_{cr, p} = σ_{cr, sl} = 95, 9 kN / {cm}^{2}

Formula 20

Sezione trasversale lorda dell'asta compressa equivalente

L'area della sezione trasversale lorda A_c del pannello della piastra irrigidito longitudinalmente è calcolata come segue, senza tenere conto delle piastre laterali supportate da una componente della piastra adiacente e dell'area della sezione trasversale efficace A_c,eff,loc,p dell'area sopra descritto:

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

Formula 21

La rigidezza appartiene alla classe della sezione trasversale 3, quindi l'area della sezione trasversale efficace della rigidezza corrisponde all'area della sezione trasversale lorda della rigidezza.

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

Formula 22

I valori della sezione trasversale sono mostrati in Figura 04.

Sezione trasversale lorda ed efficace per instabilità locale

Il coefficiente di riduzione β_a,c,p è calcolato secondo [1] , Sezione 4.5.2 come segue:

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151.6}{289, 4} = 0, 524 \end{array}

Formula 23

Il rapporto di snellezza globale λ_p della piastra irrigidita risulta, secondo [1] , equazione (4.7), in:

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{95, 9}} = 0, 440$ Formula 25	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Formula 26
	$< 0.5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Formula 27

Il rapporto di snellezza λ_p è inferiore al valore limite 0,673 secondo [1] , 4.4(2). Pertanto, non è necessaria alcuna riduzione dovuta al comportamento della soletta; ad esempio, ρ_p = 1.0.

Comportamento all'instabilità della piastra

La tensione critica elastica σ_cr,c è determinata secondo [1] , Sezione 4.5.3(3). Prima di tutto, la tensione di instabilità σ_cr,c,sl dell'irrigidimento, che è posizionato sul bordo di compressione massimo caricato, è determinata secondo [1] , Equazione (4.9).

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} = 94, 7 kN / {cm}^{2}

Formula 28

La distribuzione delle tensioni è uniforme. Pertanto, la tensione critica elastica σ_cr,c corrisponde alla tensione di instabilità elastica σ_cr,c,sl dell'irrigidimento, che è posizionato sul bordo di compressione massimo caricato.

σ_cr,c = σ_cr,c,sl = 94,7 kN/cm²

Il coefficiente di riduzione β_a,c,c è calcolato secondo [1] , punto 4.5.3(4) come segue:

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151, 6}{289, 4} = 0, 524

Formula 29

Il rapporto di snellezza λCdell'asta di compressione equivalente risulta, secondo [1] , equazione (4.11), in:

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{94, 7}} = 0, 443

Formula 31

Secondo [1] , Sezione 4.5.3(5), il raggio di inerzia i è calcolato come segue:

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11.900}{289, 4}} = 6, 41 cm

Formula 32

La distanza e è la maggiore delle due distanze secondo [1] , Figura A.1; per esempio, la distanza e₁ del singolo irrigidimento, regolata tra il baricentro e considerata indipendentemente dalla piastra, senza la larghezza efficace dall'asse baricentrico del pannello della piastra irrigidita, o la distanza e₂ dell'asse baricentrico della piastra irrigidita pannello al piano centrale della piastra. Le distanze sono mostrate in Figura 05.

Asta di compressione equivalente e irrigidimento: Distanze e1, e2

e = max (e₁, e₂ ) = max (10,39 cm, 2,86 cm) = 10,39 cm

Il coefficiente di imperfezione αe è determinato, secondo [1] , equazione (4.12) con α = 0.49, per sezioni trasversali di irrigidimento aperte come segue:

α_{e} = α \frac{0, 09}{i / e} = 0, 49 \frac{0, 09}{6, 41 / 10, 39} = 0, 636

Formula 33

Il coefficiente di riduzione χ_c è determinato secondo [3] , 6.3.1.2:

\begin{array}{l} ϕ = 0, 5 \cdot (1, 0 α_{e} \cdot ({\bar{λ}}_{c} - 0, 2) {\bar{λ}}_{c}^{2}) = 0, 5 \cdot (1, 0 0, 636 \cdot (0, 443 - 0, 2) 0, 443^{2}) = 0, 675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0, 675 \sqrt{0, 675^{2} - 0, 443^{2}}} = 0, 844 < 1 \end{array}

Formula 34

Interazione tra l'instabilità della piastra e il comportamento della placca

Il comportamento strutturale dell'intero pannello è determinato con il coefficiente ξ, secondo [1] , Sezione 4.5.4(1):

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 ma 0 \leq ξ \leq 1 \\ ξ = \frac{95, 9}{94, 7} - 1 = 0, 013 \end{array}

Formula 35

Il coefficiente di riduzione finale ρc è determinato con l'equazione di interazione secondo [1] , equazione (4.13):

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

Formula 36

Proprietà della sezione efficace

La superficie efficace della zona di compressione A_c,eff del pannello a piastra irrigidita è calcolata secondo [1] , equazione (4.5):

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

Formula 37

L'area della sezione trasversale efficace A_eff risulta in:

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

Formula 38

Sezione trasversale efficace per instabilità locale e globale

Verifica del pannello irrigidito

Gli assi baricentrici della sezione trasversale lorda e della sezione trasversale efficace non coincidono, quindi momenti flettenti agenti aggiuntivi dovuti allo spostamento dell'asse baricentrico della sezione trasversale efficace rispetto all'asse baricentrico della sezione trasversale lorda devono essere considerati qui. I momenti flettenti aggiuntivi sono calcolati come segue:

\begin{array}{l} e_{y} = 0, 82 - 0, 72 = 0, 10 cm \\ e_{z} = 164, 97 - 157, 42 = 7, 55 cm \\ M_{y} = N \cdot e_{z} = 4.000 \cdot 7, 55 = 30.202, 4 kNcm \\ M_{z} = N \cdot e_{y} = - 4.000 \cdot 0, 10 = - 414, 3 kNcm \\ M_{u} = 30.203, 7 KNcm \\ M_{v} = - 306, 4 KNcm \end{array}

Formula 39

La tensione massima risulta:

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

Formula 40

La verifica viene eseguita secondo [1] , equazione (4.15) come segue:

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5, 01}{\frac{34, 5}{1, 0}} = 0, 15

Formula 41

Verifica all'instabilità torsionale

Secondo [1] , Sezione 9.2.1(8) il seguente criterio deve essere soddisfatto in generale per evitare l'instabilità torsionale degli irrigidimenti con sezioni trasversali aperte:

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

Formula 42

I_p e I_St.Ven descrivono il momento di inerzia polare e il momento di inerzia di St. Venant della sola sezione trasversale di rigidezza (senza piastra), calcolati attorno al punto di collegamento alla piastra.

Se si considera la rigidezza da ingobbamento, è necessario determinare prima la tensione critica di instabilità torsionale σ_cr. È calcolato secondo [4] , Equazione (2.119) ed Equazione (2.120) come segue:

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

Formula 43

La rigidezza ha una costante di ingobbamento di I_ω = 0 cm⁶. La tensione critica di instabilità torsionale σ_cr è quindi semplificata in:

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

Formula 44

Secondo [1] , Sezione 9.2.1(9), il criterio in 9.2.1(8) o il seguente criterio deve essere generalmente considerato, quando si tiene conto della rigidezza di ingobbamento:

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

Formula 45

Il risultato è:

η_{2} = η_{3} = \frac{2 \cdot 34, 5}{75, 5} = 0, 91 \leq 1

Formula 46

La verifica per instabilità torsionale è quindi soddisfatta.

SHAPE-THIN

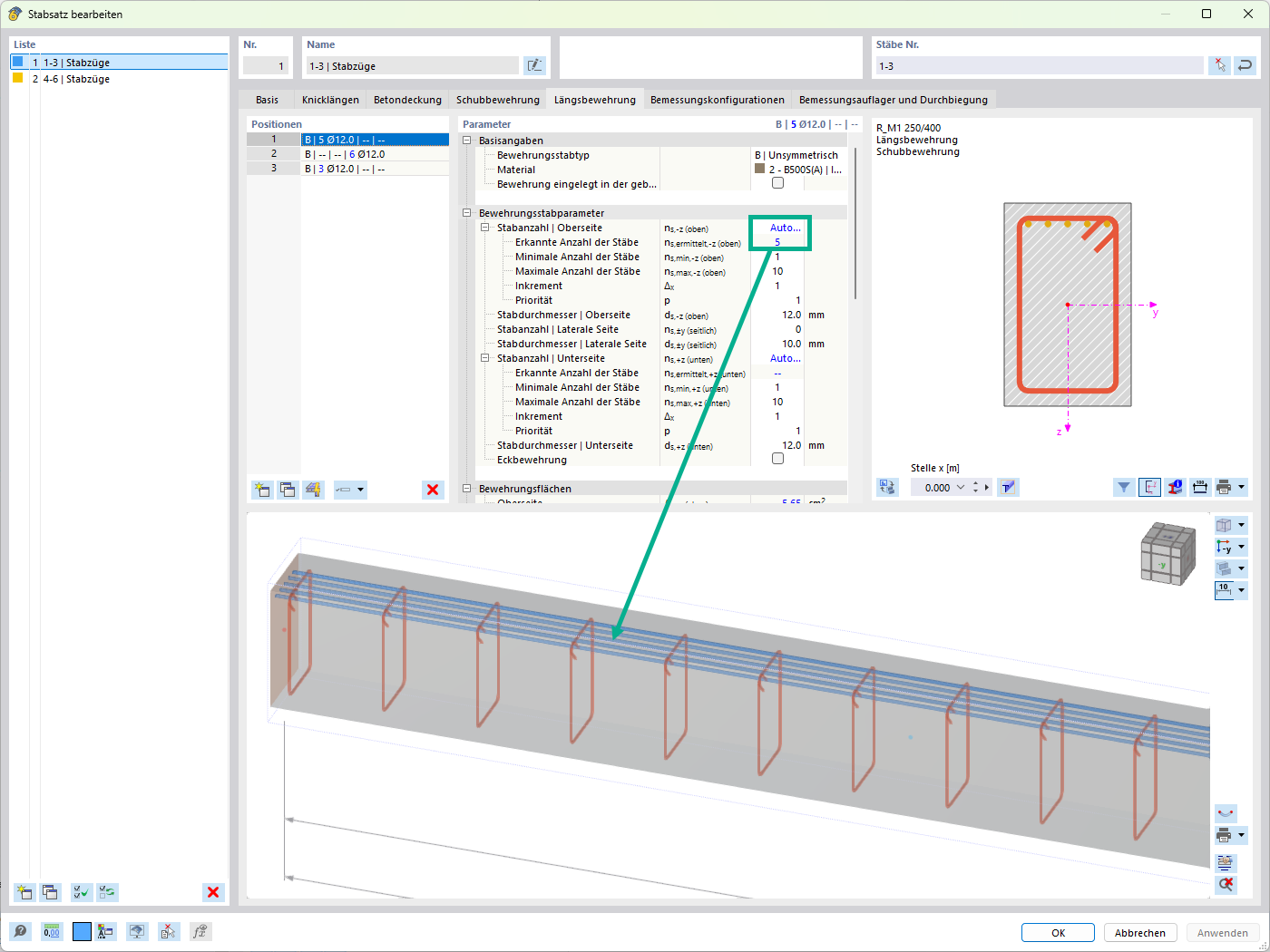
In SHAPE-THIN, il calcolo dei pannelli irrigiditi può essere eseguito secondo [1] , Sezione 4.5. Il pannello di controllo "Parti c/t e proprietà della sezione trasversale efficace" deve essere attivato nei dati generali. Successivamente, "EN 1993-1-1 e EN 1993-1-5" deve essere selezionato nei parametri di calcolo; deve essere selezionato anche il pannello di controllo intitolato "Sezione trasversale efficace secondo EN 1993-1-5, sezione 4.5". La determinazione delle larghezze efficaci dovrebbe essere eseguita in un processo iterativo secondo [1] , Sezione 4.4(3). In questo esempio, per il calcolo deve essere utilizzata solo un'iterazione in modo che anche solo un'iterazione appaia in SHAPE-THIN (vedere la Figura 07).

Calcolo dei parametri

È necessario inserire gli elementi della sezione trasversale. Le parti c/t sono generalmente generate automaticamente dalle condizioni geometriche; tuttavia, possono essere create come definite dall'utente nella tabella "1.7 Parti della sezione trasversale per la classificazione secondo EN 1993-1" (vedere la Figura 08) o nella finestra di dialogo corrispondente.

Parti della sezione trasversale per la classificazione

Gli irrigidimenti possono quindi essere definiti nella tabella "1.8 Irrigidimenti" o nella finestra di dialogo corrispondente (vedere la Figura 09).

irrigidimenti

Tuttavia, è necessario specificare il pannello irrigidito nella Tabella "1.9 Pannelli irrigiditi" (Figura 10) o nella finestra di dialogo corrispondente. È necessario selezionare gli elementi del pannello irrigidito e inserire la distanza dell'irrigidimento trasversale. Se non è definita la distanza dell'irrigidimento trasversale, per il calcolo sarà applicato il valore a = 10.000 mm. Gli irrigidimenti situati nel pannello irrigidito sono identificati automaticamente. Il pannello irrigidito deve essere vincolato all'inizio e alla fine, il che significa che è necessario un vincolo esterno.

Pannelli

I risultati della sezione trasversale efficace possono essere visti con il pulsante "Larghezze efficaci".

Ergebnisse

Autore

La signora von Bloh fornisce supporto tecnico per i nostri clienti ed è responsabile dello sviluppo del programma SHAPE‑THIN e delle strutture in acciaio e alluminio.

Link

Software di calcolo strutturale per strutture di acciaio

Bibliografia

EC 3. (2009). Eurocodice 3: Bemessung und Konstruktion von Stahlbauten – Teil 1-5: Plattenförmige Bauteile. Beuth Verlag GmbH, Berlin, 2010.
Beg, D.; Kuhlmann, U.; Davaine, L.; Braun, B.: Design of Plated Structures. Eurocode 3: Design of Steel Structures. Part 1-5 Design of Plated Structures. Berlin: Ernst & Sohn, 2011
Kuhlmann, U.: Stahlbau-Kalender 2015 - Eurocode 3 - Grundnorm, Leichtbau. Berlin: Ernst & Sohn, 2015
Johansson, B.; Maquoi, R.; Sedlacek, G.; Müller, C.; Beg, D.: Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
EC 3. (2009). Eurocodice 3: Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010

Download

File del modello usato in SHAPE-THIN

308 KB

Hai delle domande?

Eventi

2024-04-25

AISC 360-22 Verifica di collegamenti in acciaio in RFEM 6

Webinar

AISC 360-22 Verifica di collegamenti in acciaio in RFEM 6 (USA)

2024-05-15

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla verifica acciaio

2024-05-16

Considerazione delle fasi costruttive in RFEM 6

Webinar

Considerazione delle fasi costruttive in RFEM 6

2024-11-06

Corso di formazione online

RFEM 6 | Studenti | Introduzione alla verifica acciaio

Video

FAQ

[IT] FAQ 003156 | Durante il calcolo, ricevo un avviso che alcuni elementi sono collegati a ...

Durata: 00:00:52 min

Evento

Webinar | Verifica di aste in acciaio AISC 360/341-22 in RFEM 6

Durata: 01:01:43 min

Evento

Analisi di stabilità e torsione di ingobbamento (7 DOF) in RFEM 6

Durata: 00:00:00 min

Evento

Webinar | Collegamenti con sezioni cave circolari in RFEM 6

Durata: 00:00:00 min

Evento

Webinar | RWIND 2 - Calcolo dei carichi del vento con CFD Simulation

Durata: 00:00:00 min

Caratteristiche del prodotto

Coefficiente di sensibilità

Durata: 00:00:32 min

Caratteristiche del prodotto

Componente "Taglio piastra"

Durata: 00:00:53 min

Evento

Webinar | Analisi delle tensioni di modelli di scale in RFEM 6

Durata: 01:05:28 min

Caratteristiche del prodotto

Componente "Solido ausiliario"

Durata: 00:00:32 min

Playlist

Modelli da scaricare

Modello 004859 | Struttura metallica | AISC 360/341-22

223x

31x

Struttura metallica | AISC 360/341-22

3208x

214x

Base di una colonna circolare in acciaio

253x

Ponte pedonale e ciclabile a Eichsütt, Germania

299x

34x

Struttura metallica

357x

Scaffalature per campate alte, Cina

Modello 004787 | Collegamenti per strutture in acciaio

472x

53x

Collegamenti per strutture in acciaio

Modello 004778 | Trave di sollevamento di tipo H

295x

30x

Trave di sollevamento di tipo H

Silo in acciaio con carichi del vento | ASCE 7

285x

34x

Silo in acciaio con carichi del vento | ASCE 7

Modello 004746 | Struttura della copertura del palcoscenico di un teatro all'aperto

241x

37x

Struttura della copertura del palcoscenico di un teatro all'aperto

Articoli tecnici della Knowledge Base

Leggi di più

KB 001875 | AISC 341-22 Verifica di aste del telaio a momento in RFEM 6

I tre tipi di telai a momento (ordinario, intermedio, speciale) sono disponibili nell'add-on Verifica acciaio di RFEM 6. Il risultato della verifica sismica secondo AISC 341-22 è classificato in due sezioni: requisiti delle aste e dei collegamenti.

Leggi di più

L'add-on Verifica acciaio in RFEM 6 ora offre la possibilità di eseguire la verifica sismica secondo AISC 341-16 e AISC 341-22. Attualmente sono disponibili cinque tipi di sistemi resistenti alla forza sismica (SFRS).

Leggi di più

KB 001767 | AISC 341-16 Verifica dell'asta del telaio del momento in RFEM 6

I tre tipi di telai a momento (ordinario, intermedio, speciale) sono disponibili nell'add-on Verifica acciaio di RFEM 6. Il risultato della verifica sismica secondo AISC 341-16 è classificato in due sezioni: requisiti delle aste e dei collegamenti.

Leggi di più

Caratteristiche del prodotto

Caratteristica 002807 | Rappresentazione 3D dei risultati FSM

Im Dialog "Querschnitt bearbeiten" können Sie sich die Knickfiguren der Finite-Streifen-Methode (FSM) as 3D-Grafik ausgeben lassen.

Leggi di più

Verifica delle strutture di acciaio | Panoramica della verifica del sistema resistente alla forza sismica

La progettazione di cinque tipi di sistemi resistenti alla forza sismica (SFRS) include il telaio a momento speciale (SMF), il telaio a momento intermedio (IMF), il telaio a momento ordinario (OMF), il telaio ordinario concentricamente controventato (OCBF) e il telaio speciale concentricamente controventato (SCBF) )
Verifica della duttilità dei rapporti larghezza-spessore per anime e ali
Calcolo della resistenza e della rigidezza richieste per il controvento di stabilità delle travi
Calcolo della spaziatura massima per i controventi di stabilità delle travi
Calcolo della resistenza richiesta nelle posizioni delle cerniere per il controvento di stabilità delle travi
Calcolo della resistenza necessaria della colonna con l'opzione di trascurare tutti i momenti flettenti, il taglio e la torsione per lo stato limite di sovraresistenza
Verifica dei rapporti di snellezza di pilastri e controventi

Leggi di più

Add-on Verifica sismica in acciaio | Risultati

Il risultato della verifica sismica è classificato in due sezioni: requisiti delle aste e dei collegamenti.

I "Requisiti sismici" includono la resistenza a flessione richiesta e la resistenza a taglio richiesta del collegamento trave-colonna per telai a momento. Sono elencati nella scheda "Collegamento del telaio dei momenti per asta". Per i telai controventati, la resistenza a trazione del collegamento richiesta e la resistenza a compressione del collegamento richiesta del controvento sono elencate nella scheda "Collegamento controvento per asta".

Il programma fornisce le verifiche eseguite nelle tabelle. I dettagli della verifica mostrano chiaramente le formule e i riferimenti alla norma.

Leggi di più

Caratteristica 002733 | Progettazione sismica AISC 341-16 per aste in acciaio

Nel modulo Verifica calcestruzzo offre la possibilità di eseguire la verifica sismica secondo AISC 341-16 per barre di acciaio.

Per questo sono disponibili cinque tipi di SFRS (sistemi resistenti alla forza sismica).

Leggi di più

Domande frequenti (FAQ)

Qual è la differenza tra SHAPE ‑ THIN 9 e SHAPE ‑ THIN 8?

È possibile modellare sezioni piegate a freddo in SHAPE‑THIN 8 e verificarle in RF‑/STEEL Cold-Formed Sections?

Durante il calcolo, ricevo un avviso che alcuni elementi sono collegati al pannello di instabilità, ma non sono definiti come irrigidimenti (vedi Figura 01). Cosa si deve fare?

Come posso definire un vincolo plastico in RFEM 6?

Come posso scambiare dati tra RFEM 6/RSTAB 9 e IDEA StatiCa?

Come posso generare un carico superficiale sulle aste utilizzando le celle in RFEM 6 o RSTAB 9?

Progetti clienti

Prodotti consigliati per te

RFEM 6 | Programma principale RFEM 6

RFEM 6

Programma principale

La nuova generazione del software 3D agli elementi finiti viene utilizzata per l'analisi strutturale di aste, superfici e solidi.

Prezzo della prima licenza 4.170,00 USD

RFEM 6 | Verifica

Verifica acciaio per RFEM 6

Add-on

L'add-on Verifica acciaio esegue le verifiche allo stato limite ultimo e di esercizio delle aste in acciaio secondo varie norme.

Prezzo della prima licenza 2.550,00 USD

RFEM 6 | Giunti

Giunti acciaio per RFEM 6

Add-on

L'add-on Giunti acciaio per RFEM consente di analizzare i collegamenti in acciaio utilizzando un modello EF. Il modello FEM viene generato automaticamente in background e può essere controllato tramite il semplice e familiare input di componenti.

Prezzo della prima licenza 2.110,00 USD

RFEM 6 | Analisi aggiuntive

Torsione di ingobbamento (7 DOF) per RFEM 6

Add-on

L'add-on Torsione di ingobbamento (7 DOF) consente di considerare l'ingobbamento della sezione trasversale come un ulteriore grado di libertà durante il calcolo delle aste.

Prezzo della prima licenza 1.480,00 USD

RFEM 6 | Analisi aggiuntive

Comportamento non-lineare del materiale per RFEM 6

Add-on

L'add-on Comportamento non lineare del materiale consente di considerare le non linearità dei materiali in RFEM, ad esempio plastica isotropa, plastica ortotropa, danno isotropo).

Prezzo della prima licenza 1.480,00 USD

RFEM 6 | Analisi aggiuntive

Stabilità delle strutture per RFEM 6

Add-on

L'add-on Stabilità della struttura esegue l'analisi di stabilità delle strutture.

Prezzo della prima licenza 1.300,00 USD

RFEM 6 | Analisi aggiuntive

Analisi delle fasi costruttive (CSA) per RFEM 6

Add-on

L'add-on Analisi delle fasi costruttive (CSA) consente di considerare il processo di costruzione di strutture (aste, superfici e strutture solide) in RFEM.

Prezzo della prima licenza 1.570,00 USD

RFEM 6 | Analisi aggiuntive

Analisi time-dependent (TDA) per RFEM 6

Add-on

L'add-on Analisi time-dependent (TDA) consente di considerare il comportamento delle aste in base al tempo. Gli effetti a lungo termine, come viscosità, ritiro e invecchiamento, possono influenzare la distribuzione delle forze interne, a seconda della struttura.

Prezzo della prima licenza 1.030,00 USD

RFEM 6 | Analisi aggiuntive

Add-on

L'add-on Form-Finding trova la forma ottimale di aste soggette a forze assiali e modelli di superfici caricate a trazione. La forma è determinata dall'equilibrio tra la forza assiale delle aste o la tensione della membrana e le condizioni al contorno esistenti.

Prezzo della prima licenza 2.060,00 USD

RFEM 6 | Analisi dinamica

Analisi modale per RFEM 6

Add-on

L'add-on Analisi modale consente il calcolo di autovalori, frequenze naturali e periodi naturali per modelli di aste, superfici e solidi.

Prezzo della prima licenza 1.210,00 USD

RFEM 6 | Analisi dinamica

Analisi pushover per RFEM 6

Add-on

Utilizzando l'add-on Analisi pushover, è possibile analizzare le azioni sismiche su un particolare edificio e quindi valutare se l'edificio può resistere a un terremoto.

Prezzo della prima licenza 1.300,00 USD

RFEM 6 | Soluzioni speciali

Modello edificio per RFEM 6

Add-on

Le informazioni sui piani e sull'intero modello (centro di gravità) sono visualizzate in tabelle e grafici.

Prezzo della prima licenza 1.660,00 USD

RFEM 6 | Verifica

Analisi tensioni-deformazioni per RFEM 6

Add-on

L'add-on Analisi tensioni-deformazioni esegue l'analisi delle tensioni generali calcolando le tensioni esistenti e confrontandole con le tensioni limite.

Prezzo della prima licenza 1.210,00 USD

RSTAB 9 | Programma principale RSTAB 9

RSTAB 9

programma di calcolo per strutture intelaiate

Programma principale

Il moderno programma di analisi e progettazione strutturale 3D è adatto per l'analisi strutturale e dinamica di strutture a travi e per la progettazione di calcestruzzo, acciaio, legno e altri materiali.

Prezzo della prima licenza 2.910,00 USD

RSTAB 9 | Verifica

Verifica acciaio per RSTAB 9

Add-on

L'add-on Verifica acciaio esegue le verifiche allo stato limite ultimo e di esercizio delle aste in acciaio secondo varie norme.

Prezzo della prima licenza 2.550,00 USD

RSTAB 9 | Analisi aggiuntive

Stabilità delle strutture per RSTAB 9

Add-on

L'add-on Stabilità della struttura esegue l'analisi di stabilità delle strutture.

Prezzo della prima licenza 1.300,00 USD

RSTAB 9 | Verifica

Analisi tensioni-deformazioni per RSTAB 9

Add-on

L'add-on Analisi tensioni-deformazioni esegue la verifica globale delle tensioni calcolando le tensioni esistenti e confrontandole con le tensioni limite.

Prezzo della prima licenza 1.120,00 USD

RSTAB 9 | Analisi aggiuntive

Orditura a torsione (7 DOF) per RSTAB 9

Add-on

L'add-on Torsione di ingobbamento (7 DOF) consente di considerare l'ingobbamento della sezione trasversale come un ulteriore grado di libertà durante il calcolo delle aste.

Prezzo della prima licenza 1.480,00 USD

RSTAB 9 | Analisi dinamica

Analisi modale per RSTAB 9

Add-on

L'add-on Analisi modale consente il calcolo di autovalori, frequenze naturali e periodi naturali per modelli di aste, superfici e solidi.

Prezzo della prima licenza 1.210,00 USD

RSTAB 9 | Analisi dinamica

Analisi pushover per RSTAB 9

Add-on

Utilizzando l'add-on Analisi pushover, è possibile analizzare le azioni sismiche su un particolare edificio e quindi valutare se l'edificio può resistere al terremoto.

Prezzo della prima licenza 1.300,00 USD

RFEM 6 | Verifica

Verifica calcestruzzo per RFEM 6

Add-on

L'add-on Verifica calcestruzzo consente varie verifiche secondo le norme internazionali. È possibile verificare aste, superfici e pilastri ed eseguire verifiche a taglio-punzonamento e deformabilità.

Prezzo della prima licenza 2.550,00 USD

RFEM 6 | Verifica

Verifica legno per RFEM 6

Add-on

L'add-on Verifica legno esegue le verifiche allo stato limite ultimo, di esercizio e di resistenza al fuoco delle aste in legno secondo varie norme.

Prezzo della prima licenza 1.930,00 USD

RFEM 6 | Verifica

Verifica muratura per RFEM 6

Add-on

L'add-on di RFEM Verifica muratura consente di progettare strutture in muratura utilizzando il metodo degli elementi finiti. È stato sviluppato nell'ambito del progetto di ricerca intitolato DDMaS - Digitalizzazione della verifica di strutture in muratura. Il modello del materiale rappresenta il comportamento non lineare della combinazione mattone-malta sotto forma di macro modellazione.

Prezzo della prima licenza 1.660,00 USD

RFEM 6 | Verifica

Verifica alluminio per RFEM 6