Réponse:
Les coins de voile sont souvent des singularités et doivent être considérés d’un point de vue technique. Les singularités sont généralement causées par des coins rentrants et des sauts de rigidité importants.
Comme il ne s’agit pas d’un problème dans le logiciel, je ne peux expliquer qu’une méthode possible pour déterminer l’effort tranchant de calcul à l’aide d’un exemple. Comme base pour cet exemple, je m'appuie sur la littérature « Exemples de calcul selon la DIN 1045-1 ; Volume 1 : Hochbau (3. Auflage)" vom Verlag Ernst & Sohn. (Auszug finden Sie im Anhang)
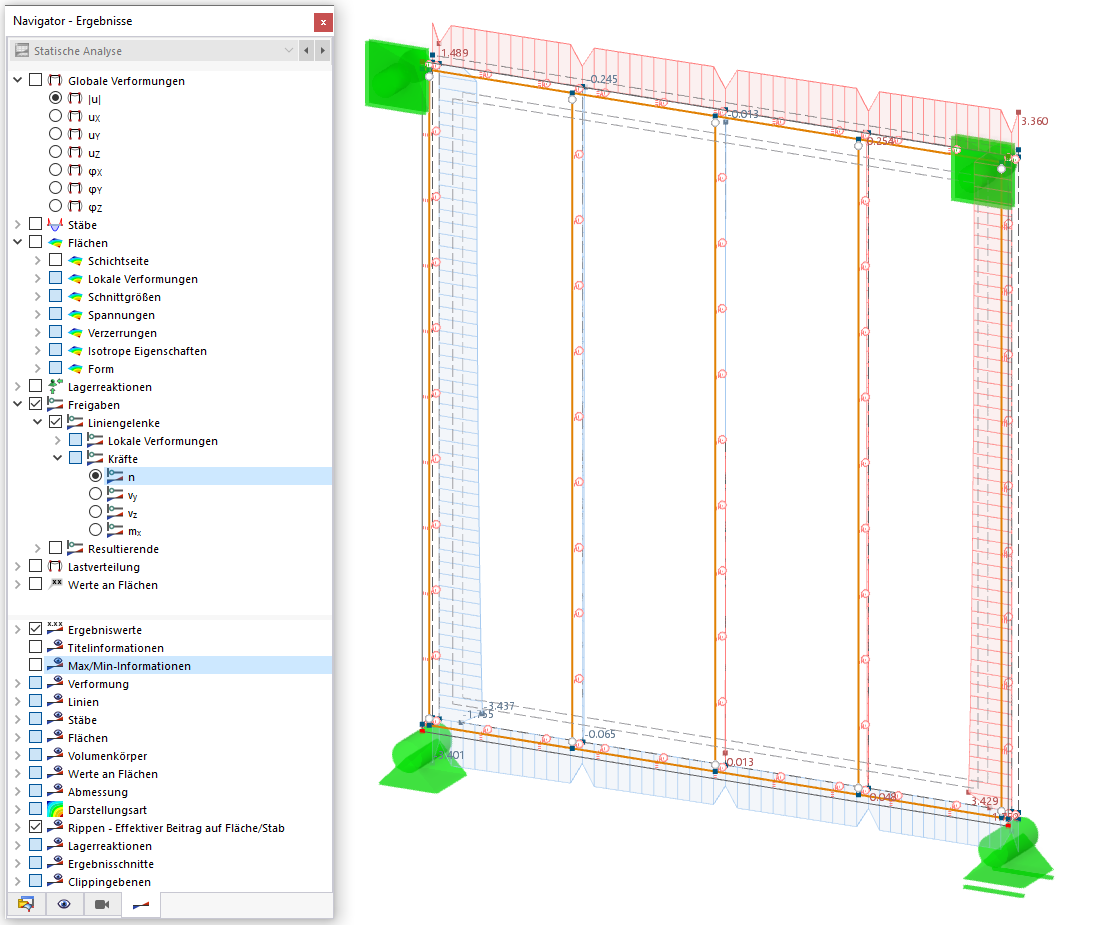
L’objectif est de déterminer l'effort tranchant de calcul dans le périmètre de contrôle. Déterminez les cotations du périmètre de contrôle selon la DIN 1045-1, Figure 38 ou Figure 39, et créez ces lignes dans RFEM (voir la Figure 01).
Pour inclure les lignes créées dans la surface, veuillez cliquer sur Calcul → Paramètres de maillage EF, puis sélectionnez l’option suivante (voir la Figure 02). Si nécessaire, effectuez un raffinement de maillage.
Après avoir calculé la combinaison de charges déterminante, sélectionnez les trois lignes droites, puis cliquez-droit sur l’une d’elles. Sélectionnez ensuite les diagrammes de résultats (voir la Figure 03).
Lassen Sie sich nun die Ergebnisse von vmax,b mit folgenden Einstellungen glätten (siehe Bild 4).
Notez la valeur lissée (209,12 kN/m sur la figure) et la longueur totale (1,05 m sur la figure). Lissez maintenant les lignes d’arc de la même manière que les lignes droites. (Es lassen sich nämlich nur Linien desselben Typs gleichzeitig auswählen um daran die Ergebnisverläufe anzeigen zu lassen.) Notieren Sie auch hier den geglätteten vmax,b (221,04 kN/m) und die Länge (0,889m). À l’aide de ces valeurs, vous pouvez maintenant déterminer l’effort tranchant pour la vérification de la résistance au poinçonnement :
vEd = β x (209,12 kN/m x 1,05 m + 221,04 x 0,889 m) / (1,05 m + 0,889 m) = 289,69 kN/m
avec = 1,35 pour les extrémités de voile et
β = 1,2 pour les coins de voile (selon la DIN 1045-1; Figure 44)
VEd = 289,69 kN/m / β x (1,05 m + 0,889 m) = 416,08 kN