Sie können die Ergebnisse für Flächen grafisch über die Navigator-Kategorie Flächen anzeigen. Die numerischen Flächenergebnisse finden Sie in der Tabellen-Kategorie Ergebnisse flächenweise.
FE-Netzknoten und Rasterpunkte
Die grafischen Ergebnisse basieren auf den Ergebnissen in den FE-Netzknoten. In der Tabelle hingegen werden die Ergebnisse in Rasterpunkten ausgegeben, die für jede Fläche definiert sind (siehe Kapitel Flächen ). Dieses Raster stellt eine vom FE-Netz unabhängige Ausgabe in Ergebnispunkten mit regelmäßigen Abständen dar.
Bei kleinen Flächen kann die Standardmaschenweite des Rasters von 0.5 m dazu führen, dass nur wenige Rasterpunkte existieren. Passen Sie in diesem Fall die Anzahl oder den Abstand der Rasterpunkte an die Flächengröße an.
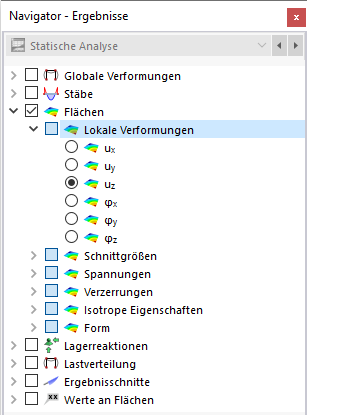
Verformungen
Das Bild Ergebnisse flächenweise in Tabelle zeigt die Tabelle mit den globalen Flächenverformungen. Diese sind auf die Achsen X, Y und Z bezogen. Die lokalen Verformungen beziehen sich auf die Flächenachsen x, y und z.
Die lokalen Verschiebungen und Verdrehungen bedeuten:
| |u| | Absolutwert der Gesamtverschiebung |
| ux | Verschiebung in Richtung der lokalen x-Achse |
| uy | Verschiebung in Richtung der lokalen y-Achse |
| uz | Verschiebung in Richtung der lokalen z-Achse |
| φx | Verdrehung um die lokale x-Achse |
| φy | Verdrehung um die lokale y-Achse |
| φz | Verdrehung um die lokale z-Achse |
Bei gekrümmten Flächen beziehen sich die Flächenachsen auf die Achsen der finiten Elemente (siehe Bild FE-Achsensysteme anzeigen).
Die Tabelle listet die Verformungen einer jeden Fläche nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind. Dort können Sie auch steuern, welche Extremwerte ausgegeben werden.
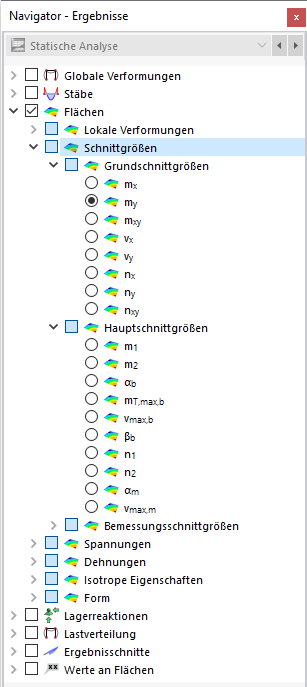
Schnittgrößen
Legen Sie im Navigator fest, welche Schnittgrößen an den Flächen dargestellt werden sollen. Die Tabelle listet die Schnittgrößen einer jeden Fläche nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.
Die Flächenschnittgrößen sind in drei Kategorien unterteilt:
- Grundschnittgrößen: Schnittgrößen in Richtung der Flächenachsen
- Hauptschnittgrößen: Schnittgrößen in Richtung der Hauptachsen
- Bemessungsschnittgrößen: Schnittgrößen nach DIN V ENV 1992-1-1, Anhang 2, A 2.8 und A 2.9
Grundschnittgrößen
Flächenschnittgrößen sind – im Unterschied zu Stabschnittgrößen – mit kleinen Buchstaben symbolisiert. Aus der Integraldefinition der Biegemomente mx und my geht hervor, dass die Momente auf die Richtungen der Flächenachsen bezogen sind, in die die entsprechenden Normalspannungen erzeugt werden.
Bei gekrümmten Flächen sind die Schnittgrößen auf die lokalen Achsen der finiten Elemente bezogen. Sie können die 'FE-Achsensysteme' im Navigator - Anzeige einblenden.
Im folgenden Bild sind die Grundschnittgrößen und Grundspannungen einer Fläche dargestellt.
Die Flächenmomente sowie die Schubspannungen senkrecht zur Fläche weisen einen parabolischen Verlauf über die Flächendicke auf.
Vorzeichen
Aus den Vorzeichen können Sie erkennen, auf welcher Flächenseite die Schnittgröße vorliegt: Zeigt die globale Z-Achse nach unten, so erzeugen positive Schnittgrößen Zugspannungen auf der positiven Flächenseite (also in Richtung der positiven Flächenachse z). Negative Schnittgrößen führen zu Druckspannungen auf der positiven Flächenseite. Ist die globale Z-Achse nach oben ausgerichtet, kehren sich die Vorzeichen entsprechend um.
Die Grundschnittgrößen sind im Kapitel 8.15 des RFEM 5-Handbuchs angegeben.
Hauptschnittgrößen
Während sich die Grundschnittgrößen auf das mehr oder weniger frei angelegte xyz-Koordinatensystem einer Fläche beziehen, stellen die Hauptschnittgrößen die Extremwerte der Schnittgrößen in einem Flächenelement dar. Zur Ermittlung der Hauptschnittgrößen werden die Grundschnittgrößen in die Richtungen der beiden Hauptachsen transformiert. Die Hauptachsen 1 (Maximalwert) und 2 (Minimalwert) sind orthogonal angeordnet.
Die Hauptschnittgrößen sind im Kapitel 8.16 des RFEM 5-Handbuchs angegeben. Sie werden aus den Grundschnittgrößen ermittelt.
Sie können die Hauptachsenrichtungen αb (für Biegemomente), βb (für Querkräfte) und αm (für Normalkräfte) grafisch als Trajektorien anzeigen.
Wenn Sie beispielsweise den Winkel αb darstellen, können Sie auch die Größen der jeweiligen Hauptmomente erkennen. Die Trajektorien sind auf die Werte der Momente m1 und m2 skaliert.
Bemessungsschnittgrößen
Die Bemessungsmomente und -normalkräfte basieren auf den in DIN V ENV 1992-1-1, Anhang 2, A 2.8 und A 2.9 vorgestellten Verfahren. Damit steht Ihnen ein Hilfsmittel für die manuelle Stahlbetonbemessung zur Verfügung. Für das Add-On 'Betonbemessung' sind die Bemessungsschnittgrößen ohne Bedeutung, da dort das Verfahren nach Baumann verwendet wird.
Die Bemessungsschnittgrößen sind im Kapitel 8.17 des RFEM 5-Handbuchs angegeben.
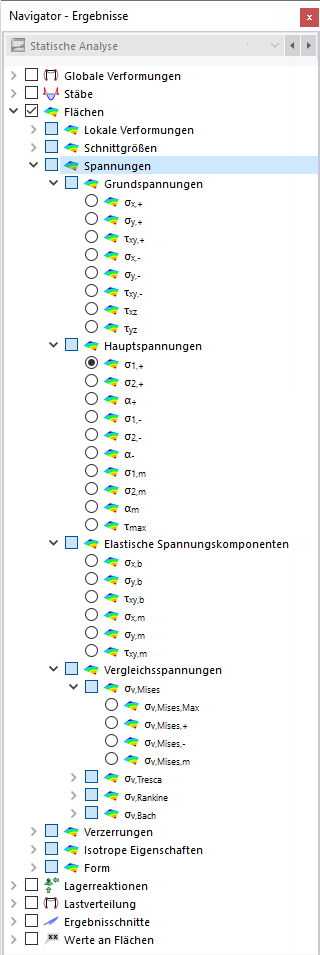
Spannungen
Legen Sie im Navigator fest, welche Spannungen an den Flächen dargestellt werden sollen. Die Tabelle listet die Spannungen einer jeden Fläche nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.
Die Flächenspannungen sind in folgende Kategorien unterteilt:
- Grundspannungen: Spannungen in Richtung der Flächenachsen
- Hauptspannungen: Spannungen in Richtung der Hauptachsen
- Elastische Spannungskomponenten: Spannungen aus Momenten und aus Normalkräften
- Vergleichsspannungen: Spannungen nach verschiedenen Vergleichsspannungshypothesen
Grundspannungen
Die Grundspannungen sind auf die Richtungen der lokalen Flächenachsen bezogen. Bei gekrümmten Flächen beziehen sie sich auf die lokalen Achsen der einzelnen finiten Elemente (siehe Bild FE-Achsensysteme anzeigen).
Die Grundspannungen sind im Kapitel 8.18 des RFEM 5-Handbuchs angegeben.
Hauptspannungen
Während sich die Grundspannungen auf das xyz-Koordinatensystem einer Fläche beziehen, stellen die Hauptschnittgrößen die Extremwerte der Spannungen in einem Flächenelement dar. Die Hauptachsen 1 (Maximalwert) und 2 (Minimalwert) sind orthogonal angeordnet.
Die Hauptschnittgrößen sind im Kapitel 8.19 des RFEM 5-Handbuchs angegeben. Sie werden aus den Grundspannungen ermittelt.
Sie können die Hauptachsenrichtungen α grafisch als Trajektorien anzeigen (vergleiche Bild Trajektorien der Hauptachsen darstellen).
Weitere Spannungen / Elastische Spannungskomponenten
Diese Kategorie enthält die Spannungsanteile infolge der Biegemomente und Membrankräfte. Sie sind auf die Richtungen der lokalen Flächenachsen bezogen.
Die Biege- und Membranspannungen sind im Kapitel 8.20 des RFEM 5-Handbuchs angegeben.
Vergleichsspannungen
Die Grundspannungen werden nach vier Vergleichsspannungshypothesen für den ebenen Spannungszustand kombiniert.
Von Mises
Die Hypothese nach von Mises wird auch als "Gestaltänderungsenergiehypothese" bezeichnet. Sie basiert auf der Annahme, dass der Werkstoff versagt, wenn die Gestaltänderungsenergie eine bestimmte Grenze überschreitet. Die Gestaltänderungsenergie stellt diejenige Energie dar, die eine Verzerrung oder Deformation des Körpers hervorruft. Dieser Ansatz stellt die bekannteste und am häufigsten angewandte Vergleichsspannungshypothese dar. Sie eignet sich für alle Materialien, die nicht spröde sind. Ein wichtiges Anwendungsgebiet ist somit der Stahlhochbau. Die Hypothese nach von Mises eignet sich nicht für hydrostatische Spannungszustände mit gleichen Hauptspannungen in alle Richtungen, da hier die Vergleichsspannung null ist.
Die Vergleichsspannungen nach von Mises sind im Kapitel 8.22 des RFEM 5-Handbuchs angegeben.
Tresca
Die Hypothese nach Tresca ist auch als "Schubspannungshypothese" bekannt. Es wird davon ausgegangen, dass das Versagen durch die maximale Schubspannung hervorgerufen wird. Da sich diese Hypothese für spröde Werkstoffe eignet, wird sie oft im Maschinenbau angewandt.
Die Vergleichsspannungen nach Tresca sind im Kapitel 8.23 des RFEM 5-Handbuchs angegeben.
Rankine
Die Vergleichsspannungshypothese nach Rankine wird auch als "Normalspannungshypothese" bezeichnet. Es wird davon ausgegangen, dass die größte Hauptspannung zum Versagen führt.
Die Vergleichsspannungen nach Rankine sind im Kapitel 8.24 des RFEM 5-Handbuchs angegeben.
Bach
Die Vergleichsspannungshypothese nach Bach wird auch als "Hauptdehnungshypothese" bezeichnet. Dabei wird davon ausgegangen, dass das Versagen in Richtung der größten Dehnung auftritt. Dieser Ansatz ähnelt der Spannungsermittlung nach Rankine. Anstelle der Hauptspannung wird hier jedoch die Hauptdehnung verwendet.
Die Vergleichsspannungen nach Bach sind im Kapitel 8.25 des RFEM 5-Handbuchs angegeben.
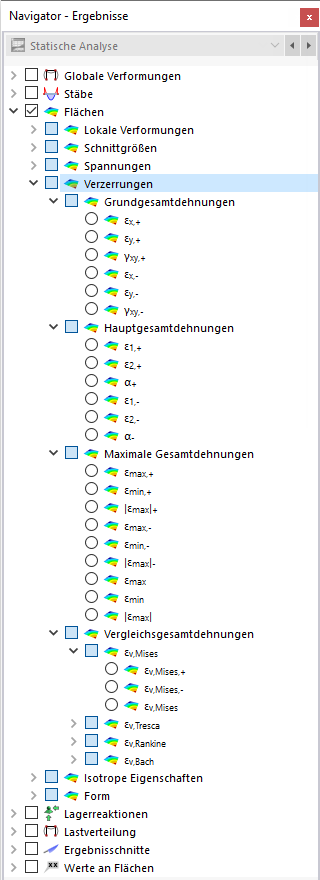
Verzerrungen
Legen Sie im Navigator fest, welche Verzerrungen an den Flächen dargestellt werden sollen. Die Tabelle listet die Dehnungen einer jeden Fläche nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.
Die Flächenverzerrungen sind in folgende Kategorien unterteilt:
- Grundgesamtdehnungen: Verzerrungen in Richtung der Flächenachsen
- Hauptgesamtdehnungen: Verzerrungen in Richtung der Hauptachsen
- Maximale Gesamtdehnungen: Extremwerte der Verzerrungen
- Vergleichsgesamtdehnungen: Verzerrungen nach verschiedenen Vergleichsspannungshypothesen
Grundgesamtdehnungen
Die Grunddehnungen sind auf die Richtungen der lokalen Flächenachsen bezogen. Bei gekrümmten Flächen beziehen sie sich auf die lokalen Achsen der einzelnen finiten Elemente (siehe Bild FE-Achsensysteme anzeigen).
Die Grunddehnungen sind im Kapitel 8.26 des RFEM 5-Handbuchs angegeben.
Hauptgesamtdehnungen
Während sich die Grunddehnungen auf das xyz-Koordinatensystem einer Fläche beziehen, stellen die Hauptdehnungen die Extremwerte der Verzerrungen in einem Flächenelement dar. Die Hauptachsen 1 (Maximalwert) und 2 (Minimalwert) sind orthogonal angeordnet.
Die Hauptdehnungen sind im Kapitel 8.27 des RFEM 5-Handbuchs angegeben. Sie werden aus den Grunddehnungen ermittelt.
Sie können die Hauptachsenrichtungen α grafisch als Trajektorien anzeigen (vergleiche Bild Trajektorien der Hauptachsen darstellen).
Maximale Gesamtdehnungen
In dieser Kategorie werden die positiven und die negativen Extremwerte der Verzerrungen ausgegeben, die sich aus den Hauptgesamtdehnungen ergeben.
Die Ermittlung der maximalen Verzerrungen ist im Kapitel 8.28 des RFEM 5-Handbuchs beschrieben.
Vergleichsgesamtdehnungen
Die Grundgesamtdehnungen werden nach vier Vergleichsspannungshypothesen für den ebenen Spannungszustand kombiniert.
Von Mises
Die Hypothese nach von Mises wird auch als "Gestaltänderungsenergiehypothese" bezeichnet. Die Gestaltänderungsenergie stellt diejenige Energie dar, die eine Verzerrung oder Deformation des Körpers hervorruft.
Die Vergleichsgesamtdehnungen nach von Mises sind im Kapitel 8.29 des RFEM 5-Handbuchs angegeben.
Tresca
Bei der Hypothese nach Tresca wird davon ausgegangen, dass das Versagen durch die maximale Schubspannung hervorgerufen wird.
Die Vergleichsgesamtdehnungen nach Tresca sind im Kapitel 8.30 des RFEM 5-Handbuchs angegeben.
Rankine
Bei der Hypothese nach Rankine wird davon ausgegangen, dass die größte Hauptspannung zum Versagen führt.
Die Vergleichsgesamtdehnungen nach Rankine sind im Kapitel 8.31 des RFEM 5-Handbuchs angegeben.
Bach
Bei der Hypothese nach Bach wird davon ausgegangen, dass das Versagen in Richtung der größten Dehnung auftritt.
Die Vergleichsgesamtdehnungen nach Bach sind im Kapitel 8.32 des RFEM 5-Handbuchs angegeben.
Kontaktspannungen
Für Flächen, die mit einem Flächenlager versehen sind, können Sie im Navigator und in der Tabelle die 'Kontaktspannungen' anzeigen lassen. Die Tabelle listet die Kontaktspannungen einer jeden Fläche nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.
Die Kontaktspannungen bedeuten:
| σz | Kontaktspannung ("Sohlpressung") in Richtung der Flächenachse z |
| τyz | Schubspannung in Richtung der Flächenachse y |
| τxz | Schubspannung in Richtung der Flächenachse x |
Die Kontaktspannungen sind im Kapitel 8.21 des RFEM 5-Handbuchs angegeben.
Die Tabelle listet die Spannungen als Kraft pro Flächeneinheit auf, die in das Flächenlager eingeleitet werden. Es handelt sich also vorzeichenmäßig nicht um die Reaktionskräfte oder -momente vonseiten des Lagers. Die Vorzeichen ergeben sich aus der Richtung der globalen Achsen. Ist die lokale Flächenachse z nach unten gerichtet, so hat der Lastfall "Eigengewicht" beispielsweise eine positive Spannung σz zur Folge. Die Vorzeichen ergeben sich damit aus der Richtung der lokalen Flächenachse z.
Summe der Lasten und Summe der Lagerkräfte
Bei Lastfällen und Lastkombinationen werden am Ende der Tabelle die Kontrollsummen Σ von Belastung und Lagerkräften angegeben. Diese Bilanz wird eine Differenz ausweisen, wenn das Modell auch Knoten-, Linien- oder Stablager aufweist. Diese Lagerkräfte sind in der Gesamtbilanz ebenfalls zu berücksichtigen.