Omezení napětí betonu v tlaku
V dialogu 1.3 Plochy je napětí betonu v tlaku omezeno na σc,max = 0,45 ⋅ fck a napětí v oceli na σs,max = 0,80 ⋅ fyk.
Für Beton C30/37 ermittelt sich damit die größte (negative) Betonspannung σc,max:
σc,max = 0.45 ∙ fck = 0.45 ∙ (-30.0) = - 13.5 N/mm2
Die vorhandene Betondruckspannung wird unter Annahme eines linearen Spannungsverlaufs ermittelt, da die Vielzahl von Iterationen zur Bestimmung der geeigneten Betondruckstrebenrichtung zu zeitaufwändig wäre. Ein linearer Verlauf ist hinreichend genau, weil im Gebrauchszustand in der Regel Betonstauchungen von maximal 0.3 bis 0.5 ‰ vorliegen.
Die maximale Spannung σc,max ist mit der vorhandenen Spannung der Betondruckzone für beide Bewehrungsrichtungen zu vergleichen.
Die vorhandene Betondruckspannung σc ermittelt sich wie folgt:
|
b |
šířka prvku (vždy 1m pro desky) |
|
αe |
účinný poměr modulů pružnosti |
|
as |
Navržená tahová výztuž |
|
d |
Staticky účinná výška |
Für die Bewehrungsrichtung φ1 ergibt sich somit folgende Druckzonenhöhe x-z,φ1:
Der gleiche Wert und die zugehörigen Zwischenwerte finden sich auch in der Detailtabelle.
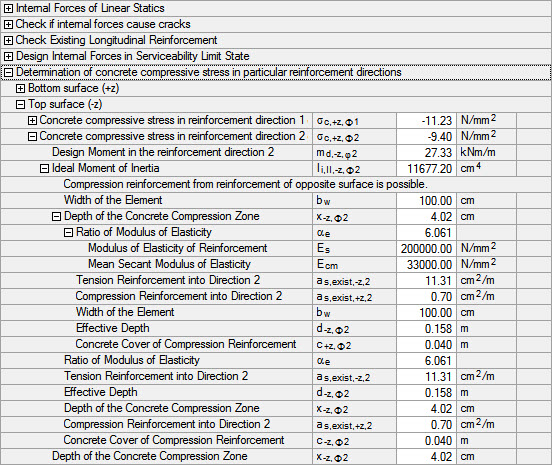
Für die Bewehrungsrichtung φ2 ergibt sich die Druckzonenhöhe x-z,φ2:
Dieser Wert und die zugehörigen Zwischenwerte sind ebenfalls bei den Details ablesbar.
Die ideellen Trägheitsmomente Ii,II im Zustand II ermitteln sich für die beiden Bewehrungsrichtungen wie folgt:
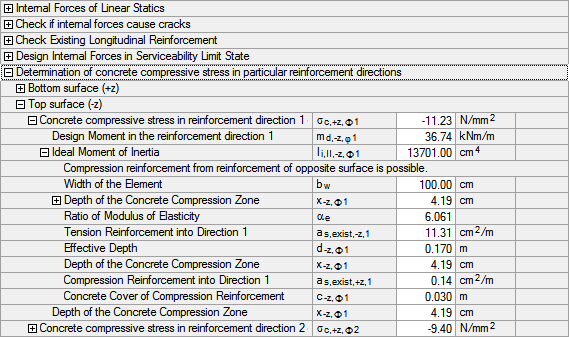
Ii,II,-z,ϕ1 = 1/3 · 100.0 · 4.193 + 6.061 · 11.31 · 17 - 4.192 = 13 701 cm4
Ii,II,-z,ϕ2 = 1/3 · 100.0 · 4.023 + 6.061 · 11.31 · 15.8 - 4.022 = 11 678 cm4
Für die beiden Bewehrungsrichtungen φ1 und φ2 ergeben sich damit gemäß Gleichung 2.69 folgende Betondruckspannungen σc in der Betondruckzone (d. h. an Flächenoberseite):
Diese Werte sind auch in Bild 2.92 ablesbar (Programm berücksichtigt mehr Nachkommastellen).
Die vorhandenen Druckspannungen σc,+z,φ1 und σc,+z,φ2 sind somit kleiner als die maximale Betonspannung σc,max (siehe Bild 2.90). Der maßgebende Quotient von vorhandener zu zulässiger Betondruckspannung liegt in die Bewehrungsrichtung φ1 vor. Der Nachweis ist erfüllt.