Autor: Mahyar Kazemian, Sajad Nikdel, Mehrnaz Mohammad Esmaeili, Vahid Nik, Kamyab Zandi
ABSTRAKT
Zatížení prostředím, jako je vítr a proudění řeky, hrají zásadní roli při statickém návrhu a posouzení statiky mostů s velkým rozpětím. Klimatické změny a extrémní klimatické jevy ohrožují spolehlivost a bezpečnost dopravní sítě.
To vedlo k rostoucí poptávce po digitálních modelech dvojčat pro zkoumání odolnosti mostů v extrémních klimatických podmínkách. Most Kalix, který byl postaven přes řeku Kalix ve Švédsku v roce 1956, je v této souvislosti použit jako zkušební základ.
Mostní konstrukce z dodatečně předpínaného betonu se skládá z pěti polí, z nichž nejdelší má 94 m. V této studii jsou získány aerodynamické charakteristiky a extrémní hodnoty numerické simulace větru, jako je například povrchový tlak, pomocí metody Spalart-Allmaras Delayed Detached Eddy Simulation (DDES) jako hybridního RANS-LES turbulentního přístupu, který je praktický i výpočetně efektivní pro blízkost stěn hustota sítě vynucená metodou LES.
Povrchový tlak větru se získá pro tři extrémní klimatické scénáře, včetně extrémního větrného počasí, extrémně chladného počasí a návrhové hodnoty pro 3000letou periodu návratu. Výsledek ukazuje na značné rozdíly v přízemním tlaku větru v důsledku časových vrstev pocházejících ze simulace nestacionárního proudění větru. Pro posouzení chování konstrukce podle kritického scénáře větru se u každého scénáře uvažuje nejvyšší hodnota povrchového tlaku.
Dále je provedena hydrodynamická studie mostních pilířů, v níž se simuluje proudění řeky metodou VOF a přechodový proces proudění vody okolo pilířů se zkoumá v různých časech. Plošný tlak, kterým působí říční proudění s největším zaznamenaným objemovým prouděním, se počítá na každém povrchu pilíře.
Při simulaci proudění řeky byly použity informace a povětrnostní podmínky zaznamenané v minulých obdobích. Výsledky ukazují, že povrchový tlak v době, kdy proudění řeky naráží na pilíře, je mnohem vyšší než v následujících dobách. Tato velikost tlaku může být použita jako kritické zatížení při výpočtech interakce kapaliny s konstrukcí (FSI).
Nakonec se pro oba úseky v různých časových krocích zobrazí povrchový tlak větru, rychlostní pole vzhledem k pomocným liniím sondy, obrysy vodního pohybu okolo sloupů a tlakový diagram na nich.
1. Úvod
Dopravní infrastruktura je páteří naší společnosti a mosty jsou úzkým hrdlem dopravní sítě [1]. Klimatické změny, které mají za následek vyšší stupeň poškození a extrémní klimatické jevy, navíc představují významnou hrozbu pro spolehlivost a bezpečnost dopravních sítí. Během posledního desetiletí bylo mnoho mostů poškozeno a zruinováno extrémními povětrnostními podmínkami, jako jsou tajfuny a povodně.
Wang a kol. analyzovali dopady změny klimatu a ukázali, že se očekává, že poškození betonových mostů bude ještě horší než dnes a že extrémní klimatické jevy budou podle předpovědi častější a s vyšší závažností [2].
Kromě toho se v průběhu času často zvyšují nároky na nosnost, například v důsledku používání těžších nákladních vozidel pro přepravu dřeva v severní Evropě a Severní Americe. Proto roste potřeba spolehlivých metod pro posouzení únosnosti konstrukce dopravní sítě v extrémních klimatických podmínkách, které zohledňují budoucí scénáře změny klimatu.
Při navrhování, výstavbě a provozu prostředků silniční dopravy se vychází z mnoha zdrojů dat a různých modelů. Konstruktéři tak používají zavedené modely stanovené normami; stavební inženýři
dokumentovat údaje o skutečném materiálu a poskytovat výkresy skutečného stavu; provozovatelé shromažďují údaje o provozu, provádějí kontroly a plánují údržbu; klimatologové kombinují klimatické údaje a modely
Předvídat budoucí klimatické jevy a hodnotitelé počítají dopad extrémního klimatického zatížení na konstrukci.
Vzhledem k převažujícím zdrojům a složitosti dat a modelů nemusí být vždy k dispozici nejaktuálnější informace a aktuální výpočty pro zásadní rozhodnutí, například pokud jde o bezpečnost konstrukce a provozuschopnost infrastruktury při mimořádných událostech. Nedostatek bezproblémové integrace mezi daty infrastruktury, statickými modely a rozhodováním na systémových úrovních je hlavním omezením současných řešení, což vede k nepřizpůsobivosti a nejistotám a vede k nákladům a neefektivitě.
Structural Digital Twin of Infrastructure je živá simulace konstrukce, která shromažďuje všechna data a modely a aktualizuje se z různých zdrojů, aby reprezentovala svůj fyzický protějšek. Konstrukční digitální dvojče, které je udržované po celou dobu životního cyklu zařízení a je kdykoli snadno přístupné, poskytuje vlastníkům/uživatelům infrastruktury včasný pohled na potenciální rizika pro mobilitu vyvolaná klimatickými jevy, těžkými nákladními automobily a dokonce i stárnutím. dopravní infrastruktury.
V rámci probíhajícího projektu vyvíjíme a implementujeme digitální dvojče pro most Kalix ve Švédsku. Hlavním cílem tohoto příspěvku je představit metodu a prostudovat výsledky kvantifikace konstrukčních zatížení v důsledku extrémních klimatických jevů na základě budoucích klimatických scénářů pro most Kalix. Most Kalix, postavený přes řeku Kalix ve Švédsku v roce 1956, je vyroben z dodatečně předpjatého betonového komorového nosníku. Most slouží jako zkušebna pro předvedení nejmodernějších metod posouzení a monitorování zdraví konstrukcí (SHM).
Specifickým cílem současného výzkumu je zohlednit klimatické parametry, jako je proudění větru a vody, které působí na konstrukce statickým a dynamickým zatížením. Naše metoda se v prvním kroku skládá ze simulace proudění větru a simulace proudění vody pomocí nestacionárního CFD modelování založeného na modelu turbulence LES/DES pro kvantifikaci zatížení větrem a vodou; to je hlavním tématem tohoto příspěvku.
V dalším kroku bude studována odezva mostu pomocí transformace profilů zatížení větrem a vodou na zatížení konstrukce při nelineární analýze konečných prvků. Nakonec bude statický model aktualizován bezproblémovým začleněním dat SHM, a vytvoří se tak statické digitální dvojče, které odráží skutečnou odezvu konstrukce. První dvě výzkumná centra zůstávají mimo bezprostřední rozsah tohoto příspěvku.
2. Popis mostu Kalix
Most Kalix se skládá z 5 dlouhých polí, z nichž nejdelší má asi 94 metrů a nejkratší 43,85 m. Most je vyroben z dodatečně předpjatého betonu, který je odléván in situ po segmentech, a z neprizmatického komorového nosníku, který je znázorněn na obrázku 1. Most má symetrickou geometrii a ve svém středu má kloub. Šířka mostovky v horní a dolní desce je asi 13 m, respektive 7,5 m. Tloušťka stěny je 45 cm a tloušťka dolní desky se pohybuje od 20 cm do
50 cm.
3. Simulace větru
Zkoušky ve větrném tunelu byly jediným způsobem, jak posoudit reakci mostů na zatížení větrem [3]; tyto experimenty jsou ovšem časově náročné a drahé. Provedení typické zkoušky ve větrném tunelu trvá přibližně 6 až 8 týdnů [4]. Nejnovější pokroky v oblasti výpočetní kapacity počítačů poskytují příležitost pro praktickou simulaci větru okolo mostů pomocí výpočetní dynamiky tekutin (CFD).
Přínosné je zkoumat tlak větru na části mostu pomocí počítačové simulace. Je třeba stanovit parametry simulace mostu a větrného pole okolo mostu; lze tak přesně vyhodnotit jejich účinky na síly působící na most.
Návrhové požadavky na mostní konstrukce vyžadují důkladné posouzení působení větru, zejména v extrémních povětrnostních podmínkách. Zajištění stability mostů s velkým rozpětím, protože jejich prvky a uspořádání jsou nejvíce náchylné k zatížení větrem, patří mezi hlavní posouzení [3].
3.1. Parametry simulace
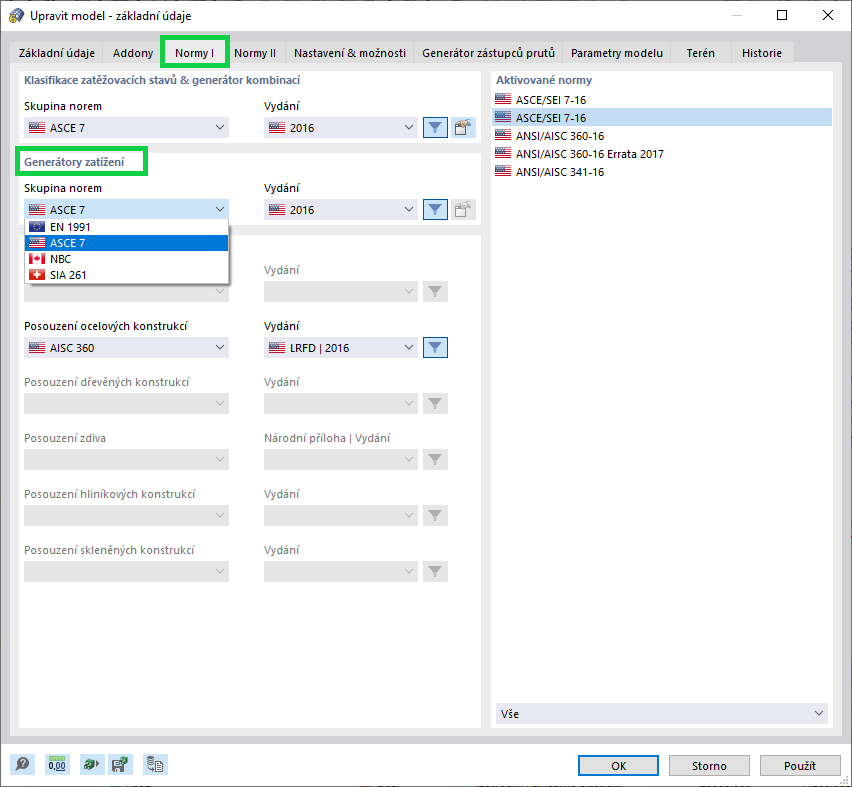
Základní rychlost větru je 22 m/s na základě větrné mapy Švédska a polohy mostu Kalix podle EN 1991-1-4 [5] a švédské normy BFS 2019:1 EKS 11; viz obrázek 1. Volná plocha nad vodou se uvažuje jako oblast vystavená zatížení větrem. Převládající směr větru je uvažován kolmo na mostovku.
Současné simulace jsou založeny na třech scénářích, které zahrnují: extrémní vítr, extrémní chlad a návrhová hodnota pro dobu návratu 3000 let. Každá podmínka má jiné hodnoty teploty, základního větru
rychlosti, kinematické viskozity a hustoty vzduchu, jak je uvedeno v tabulce 1. Soubory dat o počasí byly syntetizovány pro dva týdny extrémního počasí v průběhu 30letého období 2040-2069, přičemž bylo zohledněno 13 různých budoucích klimatických scénářů s různými globálními klimatickými modely (GCM) a reprezentativními koncentračními cestami (RCP).
Byl vybrán jeden extrémně chladný týden a jeden extrémně větrný týden
podle Nik [7]. Tento přístup byl přizpůsoben potřebám této práce s ohledem na týdenní časovou stupnici místo měsíční. Použití tohoto přístupu bylo ověřeno pro složité simulace, včetně energetických systémů [7] [8], hydrotermálních [ 9] a simulace mikroklimatu [10].
Pro zohlednění extrémních povětrnostních podmínek velmi důležité infrastruktury je třeba hodnotu základní rychlosti větru převést z 50leté periody návratu na 3000letou, jak je uvedeno v rovnici 1 [6]. Profil rychlosti a turbulence je vytvořen na základě EN 1991-1-4 [5] pro kategorii terénu 0 (Z0 = 0,003 m a Zmin = 1 m), kde Z0 a Zmin jsou délka drsnosti a minimální výška. Změna rychlosti větru s výškou je definována rovnicí 2, kde co (z) je součinitel orografie 1, vm (z) je střední rychlost větru ve výšce z, kr je součinitel terénu v závislosti na délce drsnosti a Iv (z) je intenzita turbulence; viz rovnice 3.
Hodnota rychlosti větru pro T = 3000letá perioda návratu je vypočítána na 31 m/s; tak se získají diagramy rychlosti větru a intenzity turbulence, jak je znázorněno na obrázku 2.
3.2. Model turbulence
Pro zpřesnění průzkumu proudění okolo důležitých konstrukcí, jako jsou mosty, lze použít hybridní metodu včetně DDES a výpočetně efektivní [11] [12]. Tento turbulentní model používá metodu RANS v blízkosti hraničních vrstev a metodu LES daleko od hraničních vrstev a v oddělené oblasti proudění.
V prvním kroku byla metoda simulace vírů rozšířena o získání spolehlivých předpovědí sil na modelech s velkým vlivem odděleného proudění. V přehledové části časopisu Spalart [11] uvádíme několik příkladů pro několik případů, které využívají model turbulence pro simulaci turbulence při modelování detašovaných vírů (DES).
Počáteční formulace DES [13] byla vytvořena pomocí metody Spalart-Allmaras. Pokud jde o přechod z přístupu RANS na přístup LES, je v modifikované rovnici transportu viskozity revidován termín destrukce: vzdálenost mezi bodem v definičním oboru a nejbližší plochou tělesa (d) se nahradí součinitelem zadaným vztahem:
kde CDES je součinitel, uvažuje se 0,65 a Δ je délková stupnice spojená s lokální vzdáleností rastru:
Upravený přístup DES, známý jako zpožděná simulace s vírovými víry (DDES), byl použit pro vyřešení pravděpodobného problému „separace vyvolané mřížkou“ (GIS), která souvisí s geometrií rastru. Cílem tohoto nového přístupu je potvrdit, že modelování turbulence zůstává v RANS režimu v mezních vrstvách [14]. Proto se definice parametru změní následovně:
kde fd je filtrační funkce, která udává, že hodnota 0 se zohledňuje v okrajových vrstvách blízko stěny (zóna RANS) a hodnota 1 v oblastech, kde došlo k oddělení proudění (zóna LES).
3.3. Výpočetní rastr a výsledky
Pro CFD simulaci větru se používá program RWIND 2.01 Pro, který používá externí CFD kód OpenFOAM® verze 17.10. Trojrozměrná CFD simulace se provádí jako nestacionární simulace nestlačitelného turbulentního proudění pomocí SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algoritmu.
V aktuální simulaci se jako počáteční podmínka uvažuje ustálený řešič, což znamená, že při výpočtu nestacionárního proudění se v první části simulace spustí ustálený výpočet počáteční podmínky a jakmile Po dokončení se automaticky spustí výpočet nestacionárního jevu.
Výpočetní síť se skládá z 8 057 279 buněk a 8 820 901 uzlů, přičemž se zohledňují také rozměry oblasti větrného tunelu 2000 m * 1 000 m * 100 m (délka, šířka, výška), jak je znázorněno na obrázku 3. Minimální objem buňky je 6,34*10-5 m3, maximální objem je 812,30 m3 a maximální šikmost je 1,80.
Konečný zbytkový tlak je uvažován 5*10-5. Proces generování sítě a nezávislosti rastru byl proveden pomocí čtyř velikostí sítě, které jsou znázorněny na obrázku 4 pro referenční síť, a nakonec bylo dosaženo nezávislosti na rastru.
Pro získání hodnoty tlaku větru pro extrémní povětrnostní podmínky a návrhové hodnoty větru, která je znázorněna na obrázku 5, byly provedeny tři simulace. Pro každý scénář se získá výsledek tlaku větru pomocí nestacionárního modelu turbulence DDES s dobou trvání 30 (s), který zahrnuje 60 vrstev (Δt=0,5 s).
Lze pozorovat, že přední část mostu je vystavena kladnému tlaku větru a velikost tlaku se zvyšuje o výšku blízko okraje mostovky pro všechny scénáře. Také obrázek 5. ilustruje záporné hodnoty tlaku větru zcela na povrchu desky. Hodnota pro 3000leté období je mnohem vyšší než u ostatních scénářů.
Je důležité si uvědomit, že rozsah vstupní rychlosti větru má velký vliv na hodnotu plošného tlaku spíše než na ostatní parametry. Kromě toho je třeba pro každý scénář uvažovat vyšší rozsah tlaku a sání větru během celkové doby jako kritické zatížení větrem působící na konstrukci. Nejnižší hodnota přízemního tlaku je dosažena ve scénáři extrémně chladných podmínek, zatímco v extrémních větrných podmínkách je hodnota tlaku o jeden řád vyšší.
Kromě toho je důležité si uvědomit, že chování mostu by bylo zcela odlišné v důsledku různých teplot vzduchu a možný kritický případ může nastat ve scénáři s nižším tlakem. Pokud jde o vstupní hodnotu každého scénáře, největší rozsah tlaku větru náleží návrhové úrovni vzhledem k 3000leté periodě návratu, která jako vstupní rychlost obdržela nejvyšší rychlost větru.
4. Hydrosimulace
Mostní pilíře přes řeku mohou blokovat proudění tím, že zmenšují říční průřez, vytvářejí lokální vířivé proudy a mění rychlost proudění, což může vyvíjet tlak na povrchy pilířů. Když se řeka vlévá do mostních pilířů, lze proces proudění vody okolo základny rozdělit na dvě části: působení tlaku v době, kdy voda naráží na mostní pilíř, a po počátečním tlaku, kdy voda obtéká pilíře [15].
Pokud se voda dostane určitou rychlostí k pilířům mostu, je účinek tlaku na pilíře mnohem větší než tlak kapaliny, která okolo nich zůstává. S rozvojem výpočetní techniky a se zvyšujícím se vývojem výpočetních norem pro dynamiku proudění se široce používají různé numerické simulace a ukázalo se, že výsledky mnoha simulací odpovídají výsledkům experimentů [ 16].
Proto byla v tomto výzkumu použita výpočetní metoda dynamiky tekutin pro simulaci jevů, které ovlivňují chování proudění řeky. Pro tuto studii bylo zvoleno trojrozměrné řešení založené na numerických výpočtech s použitím modelu turbulence LES. Trojrozměrná simulace proudění řeky v různých směrech a rychlostech nám umožňuje vypočítat a analyzovat všechny tlaky na povrch mostních pilířů v různých časových intervalech.
4.1. Parametry simulace
Říční proudění lze definovat jako dvoufázové proudění vody a vzduchu v otevřeném korytě. Proudění otevřeným kanálem je proudění kapaliny s volnou hladinou, na které je atmosférický tlak rovnoměrně rozdělen a je vytvářen tíhou kapaliny. Pro simulaci tohoto typu proudění se používá vícefázová metoda VOF.
Běžně dostupný program Flow3D používá metody objemových podílů VOF a FAVOF. U metody VOF se oblast modelování nejdříve rozdělí na buňky menších prvků nebo objemů ovládacích prvků. U prvků, které obsahují tekutiny, se uvažují číselné hodnoty pro každou z proudových veličin.
Tyto hodnoty představují objemový průměr hodnot v každém prvku. Ve volných povrchových proudech nejsou všechny buňky plné kapaliny; některé buňky na povrchu proudění jsou z poloviny plné. V tomto případě je definována veličina nazývaná objem kapaliny F, která představuje část buňky, která je vyplněna kapalinou.
Po stanovení polohy a úhlu plochy proudění bude možné pro výpočet pohybu tekutiny použít příslušné okrajové podmínky na hladině proudění. Jak se kapalina pohybuje, mění se s ní také hodnota F. Volné plochy jsou automaticky sledovány podle pohybu tekutiny v pevné síti. Pro stanovení geometrie se používá metoda FAVOR.
Pro stanovení výšky neobsazeného tuhého tělesa ( Vf ) lze použít také jinou objemovou veličinu. Pokud je znám objem, který zabírá tuhé těleso v každé buňce, lze hranici kapaliny v pevné síti stanovit jako VOF. Tato hranice se používá pro stanovení okrajových podmínek stěny, kterou proudění sleduje. Obecně platí, že rovnice spojitosti hmoty vypadá následovně:
Pohybové rovnice pro složky rychlosti proudění ve 3D souřadnicích, nebo jinými slovy Navier-Stokesovy rovnice, jsou následující:
kde VF je poměr otevřeného objemu k proudění, ρ je hustota kapaliny, (u, v, w) jsou složky rychlosti ve směru x, y a z, R SOR je zdrojová funkce, (Ax, Ay, Az ) jsou zlomkové plochy, ( Gx, Gy, Gz ) jsou gravitační síly, ( fx, fy, fz ) jsou viskozitní zrychlení a ( bx, by, bz ) jsou ztráty prouděním v porézním prostředí ve směru x, y a z [17].
Povodí řeky Kalix je velké a široké, a proto má subpolární klima s chladnými a dlouhými zimami a mírnými a krátkými léty. Asi 50 % srážek v této oblasti tvoří sníh. V květnu obvykle tání sněhu způsobí výrazné zvýšení průtoku řek. Klimatické podmínky řeky jsou shrnuty v tabulce 2, [18].
Na rozdíl od obecného trendu této studie se v uvedené předpovědi počasí používají informace o počasí zaznamenané v minulých obdobích. Na základě dostupných informací o počasí jsme při výpočtu definovali okrajové podmínky.
4.2Výpočetní rastr G a výsledky
Zaprvé, podle rozměrů sloupů ve třech směrech X, Y, Z a podle podélného rozměru sloupů (D = 8,5 m; viz obrázek 7) se oblast rozšíří o 10D proti směru toku a 20D po proudu. K vyřešení tohoto problému byla použita metoda strukturovaného síťování (kartézská) a software Flow3D. Pro správný rastr musí být oblast rozdělena do různých částí.
Toto rozdělení je založeno na místech se silným sklonem. Pomocí vytvoření nové plochy lze oblast rozdělit na několik částí a vytvořit tak pravidelnou síť se správnými a vhodnými rozměry, přičemž lze zadat počet buněk na každé ploše.
Tím se zvětší konečný objem buněk. Z tohoto důvodu jsme tuto oblast síťovali do tří úrovní: Hrubé, střední a jemné. Výsledky studií nezávislosti na rastru jsou znázorněny na obrázku 6. Pro kontrolu vypočítaných výsledků se musíme nejdříve ujistit, že vstupní proud je správný. Za tímto účelem se změří vstupní proudění do oblasti řešení a porovná se se základní hodnotou. Rozměry oblasti řešení jsou uvedeny na obrázku 7. Tento obrázek také přispívá k rozpoznání mostních pilířů a jejich pojmenování ploch.
Jak je znázorněno na obrázku 8, proudění řeky se nachází v přípustném rozmezí po 90 % doby simulace a rychlost vstupního proudění byla simulována správně. Kromě toho je na obrázku 9 vypočítána průměrná rychlost řeky na základě průtoku a plochy průřezu řeky.
Pro extrakci velikosti tlaku působícího na různé strany sloupů jsme zvolili časový interval simulace od 10 do 25 sekund (doba stabilizace výboje je 1800 metrů krychlových za sekundu). Vypočítané výsledky pro každou stranu jsou znázorněny na obrázcích 10 a 11. Na obrázcích 12 a 13 jsou znázorněny také rychlostní obrysy. Tyto obrysy se upravují na základě rychlosti proudění v daném čase.
Vzhledem k rozměrům oblasti řešení a rychlosti proudění řeky dosahuje proudění vody k pilířům mostu v desetině sekundy a počáteční tlak proudění působí na plochy mostních pilířů. Tento počáteční tlak se časem zmenšuje a v závislosti na ploše a procentu interakce s prouděním se na každé straně stabilizuje v určitém rozmezí. Pro výpočty interakce kapalina-konstrukce (FSI) lze použít vypočítaný kritický tlak v době, kdy proud naráží na sloupy.
5. Závěr a výhled
U mostu Kalix byly numericky zkoumány účinky extrémních povětrnostních podmínek včetně dynamického proudění větru a vody. Pro dynamické simulace větru byly definovány tři scénáře včetně extrémního větrného počasí, extrémně chladného počasí a návrhové hodnoty pro 3000letou dobu návratu. Pomocí CFD simulací byly stanoveny tlaky větru v 60 časových krocích (30 sekund) pomocí modelu turbulence DDES.
Výsledky naznačují značné rozdíly mezi jednotlivými scénáři, z nichž vyplývá důležitost vstupních dat, zejména diagramu rychlosti větru. Bylo pozorováno, že návrhová hodnota pro 3000letou dobu návratu má mnohem větší vliv než ostatní scénáře. Dále bylo ukázáno, jak je důležité zohlednit vyšší rozsah přízemního tlaku větru pomocí časových kroků pro posouzení statického chování mostu v nejkritičtějším stavu.
Kromě toho byl uvažován maximální říční proud pro simulaci nestacionárního jevu podle zaznamenaných povětrnostních podmínek a mostní pilíře byly vystaveny maximálnímu říčnímu proudu po dobu 30 sekund. Kromě fyzikálních podmínek proudění řeky a změny směru proudění ve směru toku byly kvantifikovány maximální tlaky vody v době, kdy proud naráží na pilíře.
V další práci bude vyhodnocena konstrukce mostu Kalix
zatížení větrem, tlakem vody a také dopravním zatížením, a vytváří tak digitální dvojče, které odráží skutečnou odezvu konstrukce.
6. Potvrzení
Autoři velmi oceňují podporu společnosti Dlubal Software při poskytnutí licence k programu RWIND Simulation a společnosti Flow Sciences Inc. při poskytnutí licence FLOW-3D.
Autoři
Mahyar Kazemian , doktorand, stážista na katedře inženýrství, Timezyx Inc., Kanada.
Sajad Nikdel , Ing. student, stážista na katedře inženýrství, Timezyx Inc., Kanada.
Mehrnaz Mohammad Esmaeili , student bakalářského studia, stážista na katedře inženýrství, Timezyx Inc., Kanada.
Vahid Nik , docent na katedře stavební fyziky Univerzity v Lundu a Technické univerzity v Chalmersu, Švédsko.
Kamyab Zandi , ředitel Timezyx Inc., Vancouver, BC V6N 2R2, Kanada. Email: kamyab.zandi@timezyx.com.


















..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)








































_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)


-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)


