理论背景
长细比和由此产生的折减系数根据规范EN 1993‑1‑1,第6.3章使用弹性屈曲分析方法计算,并考虑了临界屈曲荷载Ncr 。 该临界荷载是在附加模块STEEL-EC3中使用有效长度计算得出的。 对于简单结构,通常有四种欧拉情况。
对于复杂结构,有效长度评估不是那么简单。 为此可以使用RSBUCK附加模块。
首先确定结构的临界荷载系数。 通过乘以杆件的轴力就可以得到临界荷载。 相应的两个轴屈曲的有效长度可以通过以下公式计算:Ncr = E∙I∙π²/Lcr 。 最后,有效荷载系数由下式得出:kcr = Lcr/L。
RSBUCK中的全局和局部振型
下面通过一个简单的框架示例来说明确定振型,并进行正确的评估。
在确定屈曲模式和屈曲长度时,荷载起着重要作用: 屈曲值不仅取决于结构模型,而且还取决于法向力与总临界屈曲荷载Ncr的关系 。 有效长度只能对受压杆件计算。 此外,整个结构上的荷载分布会影响关键因素的确定。 通过以图形方式评估各个模态形状,您可以确定是存在全局模态形状还是局部模态形状。 如果在最不利的结构临界荷载作用下单个构件的临界荷载,则在图形中可以看出。 在这种情况下,计算结果不能用于所有其他构件,也不能进行计算。
在我们的示例中,临界荷载系数为5.32的第一个振型显示了框架在框架平面中的全局位移。 在第二种振型下的临界荷载系数是11.42,是柱子在框架平面内的局部位移(绕短轴z屈曲)。
分割杆件
在计算有效长度和有效长度系数时,必须考虑杆件的划分。 在此示例中,框架的左列由两个单个杆件组成。 由于技术建模的原因,柱子中间被分开了。 当只考虑局部振型(屈曲模式2)时,可以根据欧拉2情况和有效长度系数kcr,z = 1.0的预期结果进行分类。 但是在附加模块的结果窗口2.1中显示了两个“部分”柱子的有效长度系数k cr,z = 2.0。
这可以通过在理论背景下的关系轻松解释。 在这种情况下,整个柱子的屈曲长度等于柱子的长度,因此有效长度系数为1。 Da in RSKNICK aber Einzelstäbe ausgewertet werden, ergibt sich aus kcr = Lcr / L mit L = 0,5 ∙ Stützenlänge ein Knicklängenbeiwert von 2,0.
连续杆件的有效长度系数不能直接在RSBUCK中确定。 为此,您可以评估单个杆件的结果。 具有最小屈曲荷载Ncr的杆件可以考虑作为连续杆件的支配杆件 。 然后可以根据该杆件的有效长度和连续杆件的总长度计算k cr值。



























![膜结构的基本形状[1]](/zh/webimage/009595/2419509/01-png.png?mw=512&hash=fe42d914122820fe3c92f9595d4d91afce8a2c07)
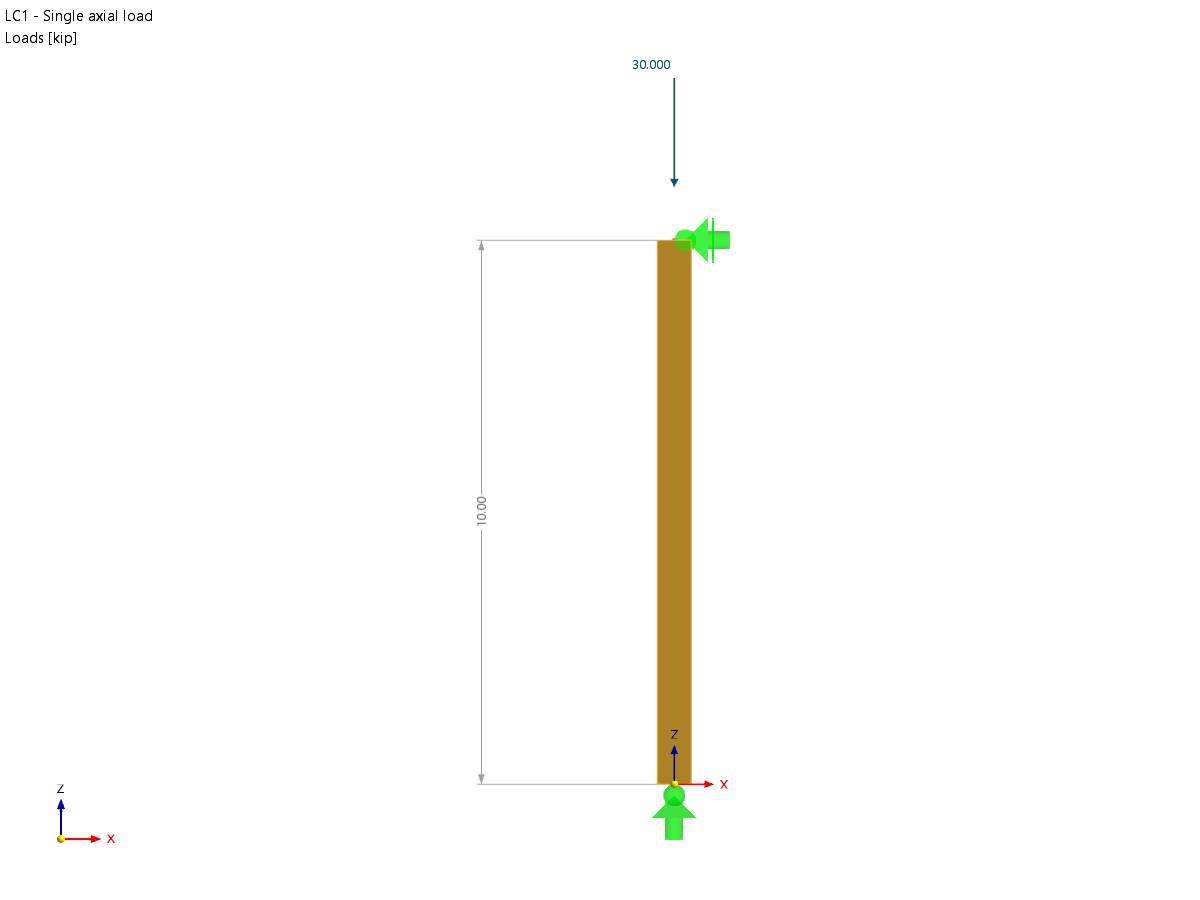









.png?mw=512&hash=ea9bf0ab53a4fb0da5c4ed81d32d53360ab2820c)

_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)



























.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)

