Exemple de calcul d’une attache rigide par platine d’about selon EN 1993-1-8

Exemple de calcul

Détermination des longueurs efficaces

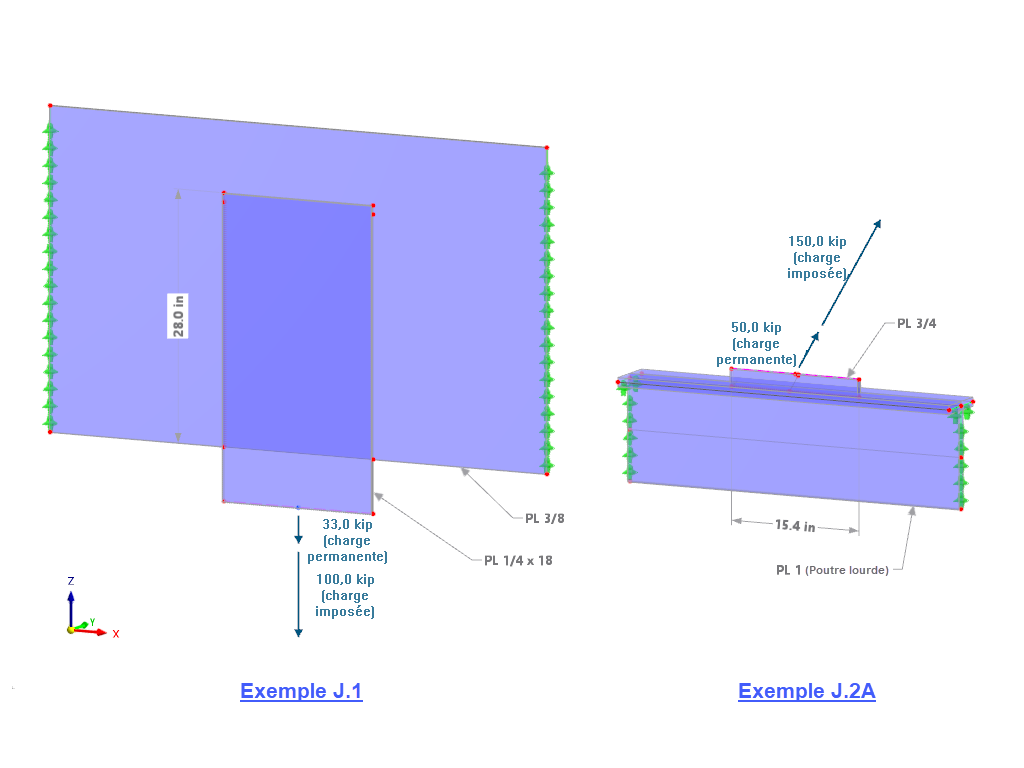
Tout d'abord, il est nécessaire de déterminer les longueurs efficaces des semelles à tronçonner selon le Tableau 6.6. La rangée de boulons inférieure n'a que peu d'effet sur la semelle comprimée en raison du très petit bras de levier et est donc négligée. Les deux rangées de boulons supérieures étant divisées par la semelle tendue de la poutre, les rangées de boulons ne doivent être considérées que séparément. Vous pouvez ainsi éviter la rupture groupée des rangées de boulons. Le calcul des longueurs efficaces requiert les paramètres e, m, ex, m_x , m₂ , b_p , w.

Paramètres des longueurs efficaces (Source : [1])

Pour cet exemple, les valeurs suivantes ont été calculées :

Dans le cas des longueurs efficaces, une distinction est faite entre les lignes de rupture circulaires et non circulaires. La configuration de la ligne de rupture linéaire requiert la valeur de la Figure 6.11. Les valeurs d'entrée sont basées sur la relation entre les bras de levier et l'âme de la poutre (λ₁ ) ou entre la semelle de la poutre (λ₂ ) et la largeur totale de la semelle en T. Les valeurs de entre deux diagrammes de la Figure 6.11 peuvent être interpolées linéairement.

Détermination de la valeur α (Source: [1])

À l'aide de ces valeurs d'entrée, les longueurs efficaces sont déterminées comme suit selon le Tableau 6.6.

Réseau de lignes d'élasticité circulaire pour la rangée de boulons extérieure :

Réseau de lignes d'élasticité circulaire pour la rangée de boulons intérieure :
l_eff,cp,i = 2 ∙ 62,6 = 393,3 mm

Réseau de lignes d'élasticité non circulaire pour la rangée de boulons extérieure :

Réseau de lignes d'élasticité non circulaire pour la rangée de boulons intérieure :
l_eff,nc,i = 6,65 62,6 = 416,3 mm

Pour déterminer la résistance de calcul en mode de défaillance 1, c'est-à-dire avec une élasticité de semelle pure, la longueur la plus courte des deux diagrammes de lignes d'élasticité est utilisée. Lors de la détermination de la résistance de calcul en mode de rupture 2, c'est-à-dire une rupture de boulon avec plastification simultanée de la semelle, seule la ligne de rupture non circulaire peut se produire.

On obtient ainsi les longueurs efficaces suivantes.

Rangée de boulons extérieure :
_leff,1,a = 150 mm
l_eff,2,a = 150 mm

Rangée de boulons intérieure :
_leff1,i = 393,3 mm
_leff2,i = 416,3 mm

Vérifier si des forces de levier peuvent se développer

Avant de déterminer la résistance de calcul de la platine en mode de défaillance 1, il faut vérifier si des forces de levier peuvent se développer. Comme cela vous permet d'obtenir des valeurs de résistance de calcul plus élevées, les dimensions et l'épaisseur du paquet de poignées doivent toujours être choisies ou modifiées de manière à ce que l'équation L_b < L_b * soit remplie. L_b est la longueur d'allongement du boulon, égale à la longueur de la poignée (épaisseur totale du matériau et des rondelles), plus la moitié de la somme de la hauteur de la tête de boulon et de la hauteur de l'écrou.

La longueur de prise, en supposant qu'un assemblage de poutre symétrique est appliqué, donne :
L_b = 2 25 + 2 4 + 0,5 19 + 0,5 15 = 75 mm

L_b * doit être déterminé séparément pour les rangées de boulons extérieures et intérieures.

Rangée de boulons extérieure :

Rangée de boulons intérieure :

Par conséquent, des forces de levier peuvent se développer dans les deux rangées de boulons.

Résistance de calcul des brides à tronçons en T

Pour le mode de défaillance « plastification complète de la semelle », la Méthode 1 de l'EN 1993-1-8 est utilisée dans cet exemple. La résistance en traction des deux semelles en T est déterminée comme suit.

Mode de défaillance « Rupture du boulon avec plastification de la semelle » :

Détermination de la résistance de calcul des semelles en T

Le mode de défaillance 2 s'applique aux deux rangées de boulons.

Rangée de boulons extérieure : 385,12 kN

Rangée de boulons intérieure : 499,24 kN

Moment résistant de l'assemblage

Les valeurs de résistance de calcul calculées pour les rangées de boulons individuelles doivent maintenant être multipliées par le bras de levier respectif jusqu'au point de compression.

Les bras de levier sont
438 mm pour la rangée de boulons extérieure,
313 mm pour la rangée de boulons intérieure.

Ainsi, le moment résistant de calcul de l'assemblage donne
M_Rd = 385,12 0,438 + 499,24 0,313 = 324,95 kNm.

Tragfähigkeiten der Schraubenreihen und zugehörige Hebelarme

Comparaison des résultats

Si cet assemblage est calculé comme un assemblage d'ossature rigide dans RF-/FRAME-JOINT Pro, la résistance de calcul résultante de la platine est de 319,79 kNm. D'après les assemblages types [2] , la résistance de calcul est de 331,3 kNm, ce qui correspond relativement bien au calcul manuel.

État limite ultime dans RF-/FRAME-JOINT Pro