Volver a la base de datos de conocimientos

16244x

001583

Sonja von Bloh, M.Sc.

12-10-2023

Diseño a fuego según la norma DIN EN 1993-1-2

La verificación de protección contra incendios puede realizarse en RF-/STEEL EC3 según EN 1993-1-2. El dimensionamiento se lleva a cabo siguiendo el método de cálculo simplificado en el nivel de capacidad portante. Se pueden elegir revestimientos con diferentes propiedades físicas como medidas de protección contra incendios. Están disponibles la curva de tiempo de temperatura estándar, la curva de incendio exterior y la curva de incendio de hidrocarburos para calcular la temperatura del gas.

La prueba de resistencia al fuego se muestra mediante un ejemplo de [3].

Ejemplo

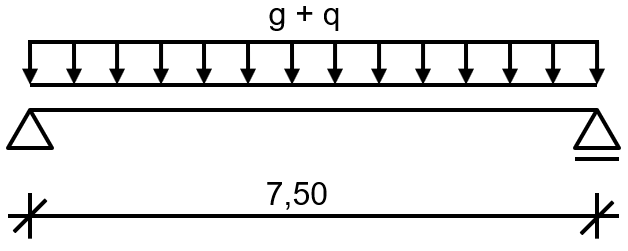
El ejemplo abarca una viga secundaria de un entrepiso. El ala superior puede considerarse como lateralmente apoyada para prevenir el pandeo lateral torsional. La clase de resistencia al fuego requerida es R30. El sistema estructural está representado en la Figura 01.

1 Sistema y cargas

Sección transversal
- HEM 280, S235, W_pl,y = 2.966 cm³
Carga
- g_k = 16,25 kN/m (carga permanente)
- q_k = 45,0 kN/m (carga útil Categoría G)

Comprobación a temperatura normal

La acción crítica es el momento en el centro del campo.

M_{y, Ed} = (γ_{G} \cdot g_{k} γ_{Q} \cdot q_{k}) \cdot \frac{l^{2}}{8}

Momento en la mitad del vano

M_{y, Ed} = (1.35 \cdot 16.25 1.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 628.86 kNm

Cálculo del momento en la mitad del vano

Clasificación de la sección transversal

La clasificación de la sección transversal se realiza según [4], Tabla 5.2.

ε = \sqrt{\frac{235}{f_{y}}} = \sqrt{\frac{235}{235}} = 1.0

Clasificación de las secciones

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 1.0 = 9

Clasificación de secciones – Ala

Alma

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 1.0 = 72

Clasificación de secciones - Alma

La sección transversal puede clasificarse como clase 1.

Valor de cálculo de la capacidad de momento

según [4] (6.13):

M_{c, y, Rd} = M_{pl, y, Rd} = \frac{W_{pl, y} \cdot f_{y}}{γ_{M 0}} = \frac{2966 \cdot 23.5}{1.0} \cdot 10^{- 2} = 697.01 kNm

valor de cálculo de la resistencia a momentos flectores

Comprobación

Comprobación según [4] (6.12):

\frac{M_{y, Ed}}{M_{c, y, Rd}} = \frac{628.86}{697.01} = 0.90 < 1

Diseño

Determinación de la temperatura del acero

Aumento de temperatura en el componente de acero no protegido

según [1] (4.25):

{Δθ}_{a, t} = k_{sh} \cdot \frac{\frac{A_{m}}{V}}{c_{a} \cdot ρ_{a}} \cdot {\overset{\cdot}{h}}_{net, d} \cdot Δt

k_sh	Coeficiente de corrección para considerar el efecto de sombra
A_m/V	Factor de la sección (representa la relación entre el área de la superficie expuesta y el volumen)
c_a	Capacidad calorífica específica
ρ_a	Densidad del acero
Δt	Intervalo para el paso de tiempo
h_net,d	flujo de calor neto

Equation EN 1993-1-2 (4.25)

Factor de perfil del componente de acero no protegido

El factor de perfil representa la relación entre la superficie no protegida y el volumen. El factor de perfil es aquí igual al perímetro del perfil de acero menos el ancho del ala superior, sombreado por el piso, en relación con el área de la sección transversal.

\frac{A_{m}}{V} = \frac{U - b}{A} = \frac{1.69 - 0.288}{0.02402} = 58.368 1 / m

Factor de la sección del componente de acero desprotegido

Factor de perfil para la caja que rodea el perfil

{(\frac{A_{m}}{V})}_{b} = \frac{2 \cdot h \cdot b}{A} = \frac{2 \cdot 0.310 \cdot 0.288}{0.02402} = 37.802 1 / m

Factor de la sección para la caja que delimita la sección

Factor de corrección para tener en cuenta el efecto de sombreado para el perfil en I

según [1] (4.26a):

k_{sh} = 0.9 \cdot \frac{{(\frac{A_{m}}{V})}_{b}}{\frac{A_{m}}{V}} = 0.9 \cdot \frac{37.802}{58.368} = 0.583

Factor de corrección para considerar el efecto de sombreado para la sección I

Curva temperatura-tiempo normalizada

según [2] (3.4):

θ_{g} = 20 345 \cdot \log_{10} (8 \cdot t 1)

curva normalizada tiempo-temperatura

Capacidad calorífica específica

Para 20 °C ≤ θ_a < 600 °C según [1] (3.2a):

c_{a} = 425 7.73 \cdot 10^{- 1} \cdot θ_{a} - 1.69 \cdot 10^{- 3} \cdot θ_{a}^{2} 2.22 \cdot 10^{- 6} \cdot θ_{a}^{3}

Capacidad calorífica específica según EN 1993-1-2 (3.2a)

Para 600 °C ≤ θ_a < 735 °C según [1] (3.2b):

c_{a} = 666 \frac{13002}{738 - θ_{a}}

Capacidad calorífica específica según EN 1993-1-2 (3.2b)

Para 735 °C ≤ θ_a < 900 °C según [1] (3.2c):

c_{a} = 545 \frac{17820}{θ_{a} - 731}

Capacidad calorífica específica según EN 1993-1-2 (3.2c)

Para 900 °C ≤ θ_a ≤ 1.200 °C según [1] (3.2d):

c_{a} = 650

Capacidad calorífica específica según EN 1993-1-2 (3.2d)

El incremento de tiempo Δt para el método de pasos de tiempo se establece en 5 s. La densidad del acero es ρ_a = 7.850 kg/m³ según [1], sección 3.2.2(1).

Flujo de calor neto

[2] (3.1)

{\overset{\cdot}{h}}_{net} = {\overset{\cdot}{h}}_{net, c} {\overset{\cdot}{h}}_{net, r}

Flujo de calor neto según EN 1991-1-2 (3.1)

[2] (3.2)

{\overset{\cdot}{h}}_{net, c} = α_{c} \cdot (θ_{g} - θ_{a})

α_c	Coeficientes de transferencia de calor por convección para la curva normalizada temperatura-tiempo α_c = 25 W/m²K según [2], 3.2.1 (2)

Flujo de calor neto según EN 1991-1-2 (3.2)

[2] (3.3)

{\overset{\cdot}{h}}_{net, r} = Φ \cdot ε_{m} \cdot ε_{f} \cdot σ \cdot [{(θ_{g} 273)}^{4} - {(θ_{a} 273)}^{4}]

ε_m	Emisividad de la superficie del componente estructural ε_m = 0.7 según [1], 4.2.5.1(3)
ε_f	Emisividad de una llama ε_f = 1.0 acc. hasta [1], 4.2.5.1(3)
σ	Constante de Stephan-Boltzmann σ = 5,67 ⋅ 10^-8 W/m² K^{4 acc.} hasta [2], 3.1(6)
Φ	Factor de configuración Φ = 1.0 acc. hasta [2], 3.1(7)

Flujo de calor neto según EN 1991-1-2 (3.3)

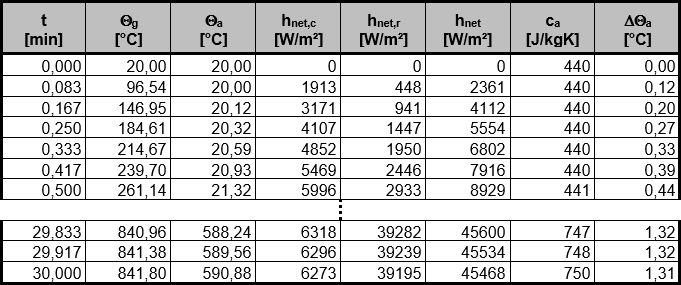
Para la temperatura del acero θ_a y la temperatura de los gases del incendio θ_g, se toma una temperatura inicial de 20 °C, temperatura ambiente. El aumento de temperatura del acero Δθ_a puede calcularse gradualmente para cada intervalo de tiempo Δt. La temperatura del acero para el siguiente paso de tiempo es la suma de la temperatura del acero del paso anterior y el aumento Δθ_a. En la Figura 02 se muestra parcialmente la evolución de la temperatura del acero.

2 Desarrollo de la temperatura del acero

La temperatura crítica del acero en el momento t = 30 min es, por tanto, θ_a = 591 °C.

Comprobación en caso de incendio

Carga crítica

Para el dimensionamiento en caso de incendio, se debe considerar la situación de diseño extraordinario. La carga crítica es el momento en el centro del campo.

M_{fi, y, Ed} = (γ_{g} \cdot g_{k} \cdot ψ_{1, 1} \cdot q_{k}) \cdot \frac{l^{2}}{8} = (1.0 \cdot 16.25 \cdot 0.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 272.46 kNm

Momento en la mitad del vano

Clasificación de la sección transversal

La clasificación de la sección transversal se puede realizar como a temperatura normal, pero con un valor reducido para ε según [1], ecuación (4.2).

ε = 0.85 \cdot \sqrt{\frac{235}{f_{y}}} = 0.85 \cdot \sqrt{\frac{235}{235}} = 0.85

Valor ε para la clasificación de la sección

Ala:

$\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 0.85 = 7.65$

Clasificación de secciones – Ala
Alma:

$\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 0.85 = 61.2$

Clasificación de secciones - Alma

La sección transversal puede clasificarse como clase 1.

Valor de cálculo de la capacidad de momento

Al determinar el valor de cálculo de la capacidad de momento, el límite de elasticidad debe reducirse debido al aumento de temperatura. A una temperatura del acero θ_a = 591 °C, el factor de reducción para el límite de elasticidad se interpola de [1], Tabla 3.1 como:

k_{y, θ} = 0.47 \frac{(0.78 - 0.47) \cdot (591 - 600)}{(500 - 600)} = 0.498

Coeficiente de reducción para el límite elástico

Para la viga no protegida, con una losa de hormigón armado en un lado y exposición al fuego en los otros tres lados, el factor de ajuste κ₁ según [1], 4.2.3.3(7) es:
κ₁ = 0,7

La temperatura se distribuye uniformemente a lo largo de la longitud. El factor de ajuste κ₂ es según [1], 4.2.3.3(8):
κ₂ = 1,0

El valor de cálculo de la capacidad de momento con distribución uniforme de temperatura es según [1], 4.2.3.3 (4.8):

M_{fi, y, θ, Rd} = k_{y, θ} \cdot \frac{γ_{M 0}}{γ_{M, fi}} \cdot M_{y, Rd} = 0.498 \cdot \frac{1.0}{1.0} \cdot 697.01 = 347.30 kNm

Momento resistente de cálculo con distribución de temperatura uniforme

El valor de cálculo de la capacidad de momento con distribución no uniforme de temperatura es según [1], 4.2.3.3 (4.10):

M_{fi, y, t, Rd} = \frac{M_{fi, y, θ, Rd}}{κ_{1} \cdot κ_{2}}; M_{fi, y, θ, Rd} \leq M_{y, Rd}

M_{fi, y, t, Rd} = \frac{347.30}{0.7 \cdot 1.0} = 496.15 kNm

Momento resistente de cálculo con una distribución de temperatura no uniforme

Comprobación

Comprobación según [1] (4.1):

\frac{M_{fi, y, Ed}}{M_{fi, y, t, Rd}} = \frac{272.46}{496.15} = 0.55 < 1.0

Diseño EN 1993-1-2 (4.1)

RF-/STAHL EC3

El ejemplo se calcula en RF-/STAHL EC3. Los archivos de modelo correspondientes para RFEM y RSTAB están disponibles para descargar al final del artículo.

Datos básicos

Se dimensiona la barra 1. Para el dimensionamiento a temperatura normal, se selecciona en la pestaña "Capacidad de carga" las combinaciones de carga para la situación de diseño permanente/temporal según la ecuación 6.10; y para el dimensionamiento en caso de incendio, se seleccionan en la pestaña "Resistencia al fuego" las combinaciones de carga para la situación de diseño extraordinaria según la ecuación 6.11c (Figura 03).

3 Ventana 1.1 Datos generales

Longitudes efectivas - Barras

Se impide el pandeo lateral torsional, por lo que en la pestaña "1.5 Longitudes efectivas - Barras" se desactiva la casilla correspondiente (Figura 04).

4 Ventana 1.5 Longitudes - Barras

Detalles

La duración requerida de la resistencia al fuego, la curva de temperatura y los coeficientes para determinar el flujo de calor neto se configuran en la pestaña "Resistencia al fuego" del cuadro de diálogo "Detalles" (Figura 05).

5 Cuadro de diálogo Detalles, pestaña Resistencia al fuego: Configuración del cálculo frente al fuego

Resistencia al fuego - Barras

Los parámetros de resistencia al fuego, como la exposición al fuego y las medidas de resistencia al fuego, se definen en la pestaña "1.10 Resistencia al fuego - Barras" (Figura 06). La viga no protegida está expuesta al fuego por tres lados.

6 Ventana 1.10 Resistencia al fuego - Barras

Resultados

Los resultados se muestran después del cálculo (Figura 07). También se presentan los valores intermedios relevantes para el dimensionamiento en caso de incendio, como la temperatura del acero, etc., en la tabla "Valores intermedios".

7 Resultados

Autor

Sra. von Bloh proporciona soporte técnico a nuestros clientes y es responsable del desarrollo del programa SHAPE-THIN, así como de las estructuras de acero y aluminio.

Enlaces

Software de análisis para estructuras de acero

Referencias

Eurocódigo 3: Diseño de estructuras de acero - Parte 1-2: Allgemeine Regeln - Tragwerksbemessung für den Brandfall. Beuth Verlag GmbH, Berlin, 2010.
Comité Europeo de Normalización (2002). Eurocódigo 1: Einwirkungen auf Tragwerke - Teil 1-2: Allgemeine Einwirkungen - Brandeinwirkungen auf Tragwerke. Berlín: Beuth.
Mensinger, M. y Stadler, M. Brandschutznachweise - Workshop Eurocode 3 - Rechenbeispiele. Munich: Technische Universität München, Lehrstuhl für Metallbau, 2008
Eurocódigo 3: Cálculo de estructuras de acero, parte 1‑1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010

Descargas

Archivo del modelo de RFEM

388 KB

Archivo del modelo de RSTAB

340 KB

Análisis de estructuras en riesgo de incendio

;