14201x

001583

Sonja von Bloh, M.Sc.

31.07.2019

Calcul de la résistance au feu selon la norme DIN EN 1993-1-2

RF-/STEEL EC3 permet de vérifier la résistance au feu selon l'EN 1993-1-2. Le calcul est effectué selon la méthode de calcul simplifiée à l'ELU. Des revêtements ayant des propriétés physiques différentes peuvent être sélectionnés comme mesures de protection contre les incendies. La courbe température-temps standard, la courbe de feu externe et la courbe hydrocarbure peuvent être sélectionnées pour déterminer la température du gaz.

Ce calcul de la résistance au feu est illustré à l'aide d'un exemple tiré de {%}#Refer [31]]].

Exemple

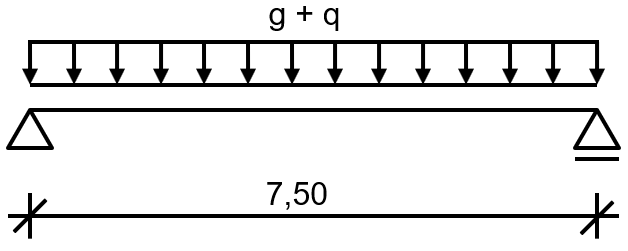
Cet exemple inclut une poutre secondaire de plafond intermédiaire. On peut supposer que la semelle supérieure a des maintiens latéraux pour éviter le déversement. La classe de résistance au feu requise est la classe R30. La Figure 01 représente cette structure.

1 Système et chargement

Section
- HEM 280, S235, W_pl,y = 2.966 cm³
Hypothèse de charge
- g_k = 16,25 kN/m (charge permanente)
- q_k = 45,0 kN/m (catégorie de la charge d'exploitation G)

Vérification à des conditions de température normales

L'action déterminante est le moment au milieu de la travée.

M_{y, Ed} = (γ_{G} \cdot g_{k} γ_{Q} \cdot q_{k}) \cdot \frac{l^{2}}{8}

Moment au milieu de la travée

M_{y, Ed} = (1.35 \cdot 16.25 1.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 628.86 kNm

Calcul du moment au milieu de la travée

Classification des sections

La classification de la section est basée sur le Tableau 5.2 [4].

ε = \sqrt{\frac{235}{f_{y}}} = \sqrt{\frac{235}{235}} = 1.0

Classification des sections

Semelle

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 1.0 = 9

Classification de la section - Semelle

Âme

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 1.0 = 72

Classification de la section - Âme

La section peut être assignée à la classe 1.

Valeur de calcul de la résistance aux moments

Selon [4] (6.13) :

M_{c, y, Rd} = M_{pl, y, Rd} = \frac{W_{pl, y} \cdot f_{y}}{γ_{M 0}} = \frac{2966 \cdot 23.5}{1.0} \cdot 10^{- 2} = 697.01 kNm

Valeur de calcul de la résistance aux moments

Conception

Vérification selon [4] (6.12) :

\frac{M_{y, Ed}}{M_{c, y, Rd}} = \frac{628.86}{697.01} = 0.90 < 1

Conception

Détermination de la température de l'acier

Augmentation de la température dans le composant en acier non protégé

Selon [1] (4.25) :

{Δθ}_{a, t} = k_{sh} \cdot \frac{\frac{A_{m}}{V}}{c_{a} \cdot ρ_{a}} \cdot {\overset{\cdot}{h}}_{net, d} \cdot Δt

k_sh	Facteur de correction pour la considération de l'effet d'ombre
A_m/V	Facteur de section (rapport entre la surface exposée et le volume)
c_a	Capacité de chaleur spécifique
ρ_a	Densité de l'acier
Δt	Intervalle pour le pas de temps
h_net,d	Flux thermique net

Équation EN 1993-1-2 (4.25)

Facteur de section du composant en acier non protégé

Le facteur de section désigne le rapport entre la surface exposée et le volume. Le facteur de section est ici égal à la circonférence de la section en acier moins la largeur de la semelle supérieure, ombragée par le plafond, par rapport à l'aire de la section.

\frac{A_{m}}{V} = \frac{U - b}{A} = \frac{1.69 - 0.288}{0.02402} = 58.368 1 / m

Facteur de section du composant en acier non protégé

Facteur de section pour le caisson entourant la section

{(\frac{A_{m}}{V})}_{b} = \frac{2 \cdot h \cdot b}{A} = \frac{2 \cdot 0.310 \cdot 0.288}{0.02402} = 37.802 1 / m

Facteur de section pour le caisson entourant la section

Facteur de correction pour la considération de l'effet d'ombre pour la section en I

Selon [1] (4.26a) :

k_{sh} = 0.9 \cdot \frac{{(\frac{A_{m}}{V})}_{b}}{\frac{A_{m}}{V}} = 0.9 \cdot \frac{37.802}{58.368} = 0.583

Facteur de correction pour la considération de l'effet d'ombre pour la section en I

Courbe température/temps normalisée

Selon [2] (3.4) :

θ_{g} = 20 345 \cdot \log_{10} (8 \cdot t 1)

Courbe température/temps normalisée

Capacité de chaleur spécifique

Pour 20 °C ≤ θ_a < 600 °C selon {%}#Refer [1]]] (3.2a) :

c_{a} = 425 7.73 \cdot 10^{- 1} \cdot θ_{a} - 1.69 \cdot 10^{- 3} \cdot θ_{a}^{2} 2.22 \cdot 10^{- 6} \cdot θ_{a}^{3}

Capacité thermique spécifique selon l'EN 1993-1-2 (3.2a)

Pour 600 °C ≤ θ_a < 735 °C selon {%}#Refer [1]]] (3.2b) :

c_{a} = 666 \frac{13002}{738 - θ_{a}}

Capacité thermique spécifique selon l'EN 1993-1-2 (3.2b)

Pour 735°C ≤ θ_a < 900 °C selon {%}#Refer [1]]] (3.2c) :

c_{a} = 545 \frac{17820}{θ_{a} - 731}

Capacité thermique spécifique selon l'EN 1993-1-2 (3.2c)

Für 900°C ≤ θ_a ≤ 1 200°C selon [1] (3.2d) :

c_{a} = 650

Capacité thermique spécifique selon l'EN 1993-1-2 (3.2d)

L'intervalle Δt sélectionné pour la méthode du pas de temps est de 5 s. La masse volumique de l'acier est ρ_a = 7 850 kg/m³ selon la Section 3.2.2 (1) de [1].

Flux thermique net

[2] (3.1)

{\overset{\cdot}{h}}_{net} = {\overset{\cdot}{h}}_{net, c} {\overset{\cdot}{h}}_{net, r}

Flux thermique net selon l'EN 1991-1-2 (3.1)

[2] (3.2)

{\overset{\cdot}{h}}_{net, c} = α_{c} \cdot (θ_{g} - θ_{a})

α_c	Coefficients de transfert thermique par convection pour la courbe température-temps standard α_c = 25 W/m²K selon [2], 3.2.1 (2)

Flux thermique net selon l'EN 1991-1-2 (3.2)

[2] (3.3)

{\overset{\cdot}{h}}_{net, r} = Φ \cdot ε_{m} \cdot ε_{f} \cdot σ \cdot [{(θ_{g} 273)}^{4} - {(θ_{a} 273)}^{4}]

ε_m	Émissivité de la surface du composant structural ε_m = 0,7 selon [1], 4.2.5.1 (3)
ε_f	Émissivité d'une flamme ε_f = 1,0 selon. à [1], 4.2.5.1 (3)
σ	Constante de Stephan-Boltzmann σ = 5,67 ⋅^10-8 W/m² K^{4 selon} à [2], 3.1 (6)
Φ	Facteur de configuration Φ = 1,0 selon à [2], 3.1 (7)

Flux thermique net selon l'EN 1991-1-2 (3.3)

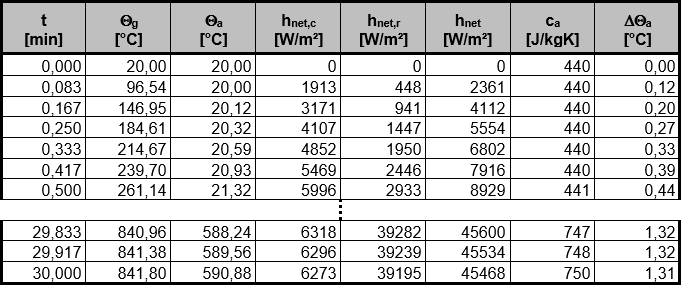
La température de départ est présumée être une température ambiante de 20°C pour la température de l'acier θ_a et la température des gaz θ_g. L'augmentation de la température de l'acier Δθ_a peut être calculée pas à pas pour chaque intervalle de temps Δt. La température de l'acier pour le pas de temps suivant est obtenue à partir de la somme de la température de l'acier à l'étape précédente et de l'augmentation de la température Δθ_a. La Figure 02 montre une vue partielle de l'évolution de la température de l'acier.

2 Évolution de la température de l'acier

La température déterminante de l'acier au moment t = 30 min est ainsi θ_a = 591°C.

Vérification en cas d'incendie

Action déterminante

La situation de projet accidentelle doit être utilisée pour la vérification de la résistance au feu. L'action déterminante est le moment au milieu de la travée.

M_{fi, y, Ed} = (γ_{g} \cdot g_{k} \cdot ψ_{1, 1} \cdot q_{k}) \cdot \frac{l^{2}}{8} = (1.0 \cdot 16.25 \cdot 0.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 272.46 kNm

Moment au milieu de la travée

Classification des sections

Pour l'application de ces règles simplifiées, les sections peuvent être classées comme pour le calcul à température normale en considérant la valeur réduite de ε donnée dans l'Équation (4.2) [1]).

ε = 0.85 \cdot \sqrt{\frac{235}{f_{y}}} = 0.85 \cdot \sqrt{\frac{235}{235}} = 0.85

Valeur ε pour la classification des sections

Semelle :

$\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 0.85 = 7.65$

Classification de la section - Semelle
Âme :

$\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 0.85 = 61.2$

Classification de la section - Âme

La section peut être assignée à la classe 1.

Valeur de calcul de la résistance aux moments

Lors de la détermination de la valeur de calcul de la résistance aux moments, la limite d'élasticité doit être réduite en raison de l'augmentation de température. Pour une température de l'acier_θa = 591 °C, le facteur de réduction pour la limite d'élasticité est interpolé à partir du Tableau 3.1 de {%}#Refer [1]]] :

k_{y, θ} = 0.47 \frac{(0.78 - 0.47) \cdot (591 - 600)}{(500 - 600)} = 0.498

Coefficient de réduction pour la limite d'élasticité

Pour la poutre non protégée avec une dalle en béton armé d'un côté et exposée au feu des trois autres côtés, le facteur d'adaptation κ₁ selon [1], 4.2.3.3 (7) permet d'obtenir :
κ₁ = 0,7

La température est répartie uniformément sur toute la longueur de la poutre. Le facteur d'ajustement κ₂ selon la section 4.2.3.3 (8) de [1]) permet d'obtenir le résultat suivant :
κ₂ = 1,0

La valeur de calcul du moment résistant avec répartition uniforme de la température est la suivante selon la section 4.2.3.3 (4.8) de [1]) :

M_{fi, y, θ, Rd} = k_{y, θ} \cdot \frac{γ_{M 0}}{γ_{M, fi}} \cdot M_{y, Rd} = 0.498 \cdot \frac{1.0}{1.0} \cdot 697.01 = 347.30 kNm

Résistance de calcul au moment avec distribution de température uniforme

La valeur de calcul du moment résistant avec répartition inégale de la température est la suivante selon la section 4.2.3.3 (4.10) de [1]) :

M_{fi, y, t, Rd} = \frac{M_{fi, y, θ, Rd}}{κ_{1} \cdot κ_{2}}; M_{fi, y, θ, Rd} \leq M_{y, Rd}

M_{fi, y, t, Rd} = \frac{347.30}{0.7 \cdot 1.0} = 496.15 kNm

Résistance de calcul au moment avec répartition inégale de la température

Conception

Vérification selon [1] (4.1) :

\frac{M_{fi, y, Ed}}{M_{fi, y, t, Rd}} = \frac{272.46}{496.15} = 0.55 < 1.0

Vérification selon l'EN 1993-1-2 (4.1)

RF-STEEL EC3

Cet exemple est calculé dans RF-/STEEL EC3. Les fichiers des modèles RFEM et RSTAB correspondants sont disponibles dans la section « Téléchargements » au bas de cet article.

Données de base

La barre 1 est calculée. Pour le calcul à température normale, sélectionnez les combinaisons de charges pour la situation de projet permanente/transitoire selon l'équation 6.10 dans l'onglet « État limite ultime » et les combinaisons de charges pour la situation de projet accidentelle selon l'équation 6.11c pour la vérification de la résistance au feu dans l'onglet « Résistance au feu » (Figure 03).

3 Fenêtre 1.1 Données de base

Longueurs efficaces - Barres

Le déversement est évité de sorte que la case correspondante soit décochée dans la fenêtre « 1.5 Longueurs efficaces - Barres » (Figure 04).

4 Fenêtre 1.5 Longueurs efficaces - Barres

Détails

Le temps requis pour la résistance au feu, la courbe de température et les coefficients pour déterminer le flux thermique net sont définis dans l'onglet « Résistance au feu » de la boîte de dialogue « Détails » (Figure 05).

5 Boîte de dialogue Détails, onglet Résistance au feu : Paramètres pour la vérification de la résistance au feu

Résistance au feu - Barres

Définissez les paramètres de résistance au feu tels que l'exposition au feu et les mesures de protection contre l'incendie dans la fenêtre « 1.10 Résistance au feu - Barres » (Figure 06). La poutre non protégée est exposée au feu sur trois côtés.

6 Fenêtre 1.10 Résistance au feu - Barres

Résultats

les résultats sont affichés au terme du calcul (Figure 07). Les valeurs intermédiaires pertinentes pour la vérification de la résistance au feu, telles que la température de l'acier, sont également affichées dans le tableau « Détails ».

7 Résultats

Auteur

Mme von Bloh fournit une assistance technique à nos utilisateurs et est également responsable du développement du programme SHAPE-THIN et de la construction en acier et en aluminium.

Liens

Logiciels de calcul de structures en acier

Références

Eurocode 3 : calcul des structures en acier - Partie 1-2 : Règles générales – Vérification du comportement au feu , EN 1993-1-2. Berlin : Beth, 1993
EN 1991-1-2 Eurocode 1 : Actions sur les structures - Partie 1‑2: Actions générales - Actions du feu sur les structures. Berlin : Beth, 1993
Desinger, M.; Stadler, M. Brandschutznachweise - Workshop Eurocode 3 - Rechenbeispiele. Munich : Technische Universität München, Lehrstuhl für Metallbau, 2008
Eurocode 3 : Eurocode 3: Calcul des structures en acier - Partie 1‑1: Règles générales et règles pour les bâtiments. (2010) Berlin : Beth Verlag GmbH

Téléchargements

Fichier du modèle RFEM

388 KB

Fichier du modèle RSTAB

340 KB

;