Si se activa el complemento Análisis de comportamiento de material no lineal (se requiere licencia) en Modelo - Datos básicos, hay más opciones para la selección en la lista de modelos de material además del 'Isótropo | Elástico lineal' y 'ortótropo | Elástico lineal'.
Si utiliza modelos de material no lineal en RFEM, siempre se realiza un cálculo iterativo. Dependiendo del modelo de material, se define una relación diferente entre las tensiones y deformaciones.
La rigidez de los elementos finitos se ajustará una y otra vez en el transcurso de las iteraciones hasta que se cumpla la relación tensión-deformación. El ajuste se realiza siempre para toda una superficie o elemento sólido. Por lo tanto, recomendamos usar siempre el tipo de suavizado Constante en elementos de malla al evaluar las tensiones.
Algunos modelos de material en RFEM se indican con 'Plástico', otros con 'Elástico no lineal'.
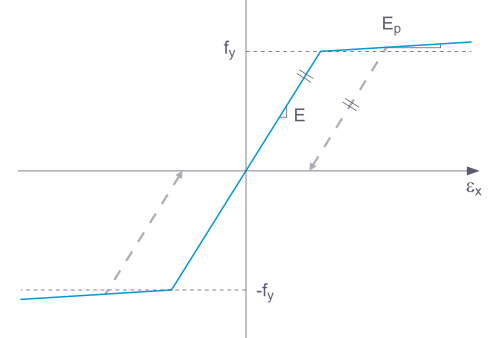
Si un componente estructural con un material elástico no lineal se libera nuevamente, la deformación regresa por el mismo camino. Tras una descarga total, no queda deformación.
Al descargar un componente estructural con un modelo de material Plástico, la deformación permanece después de que se haya descargado por completo.
Puede encontrar información básica sobre los modelos de materiales no lineales en el artículo técnico que describe las modelo de material.
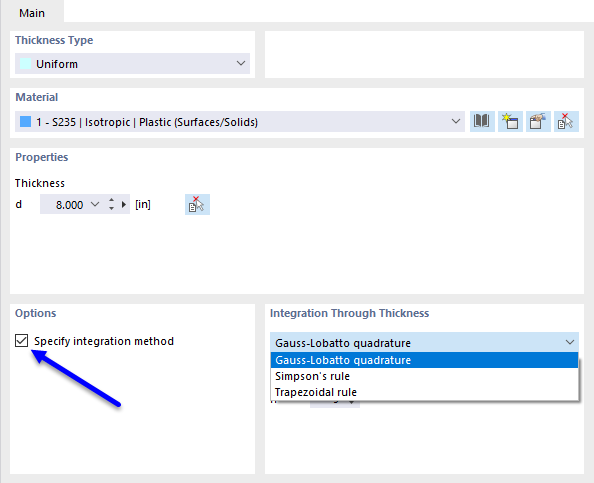
Los esfuerzos internos y momentos en placas con material no lineal resultan de la integración numérica de las tensiones sobre el espesor d de la placa. Para definir el método de integración para el espesor, seleccione la opción Especificar método de integración en el cuadro de diálogo 'Editar espesor'. Están disponibles los siguientes métodos de integración:
- Cuadratura de Gauss-Lobatto
- Regla de Simpson
- Regla trapezoidal
Además, puede especificar el 'Número de puntos de integración' de 3 a 99 según el espesor de la placa.
Isótropo plástico (barras)
Al seleccionar el Isótropo | Plástico (barras) en la lista desplegable 'Modelo de material', se activa la pestaña para introducir parámetros de material no lineal.
En esta pestaña, define el diagrama tensión-deformación, estando disponibles las siguientes opciones:
- Fundamentos básicos
- Bilineal
- Diagrama tensión-deformación
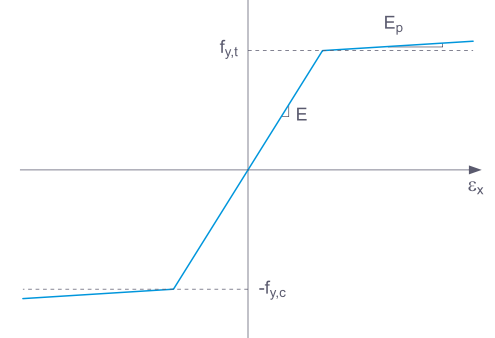
Si se selecciona Básico ', RFEM usa un modelo de material bilineal. Los valores de la base de datos de materiales se utilizan para el módulo de elasticidad E y el límite elástico fy Por razones numéricas, la rama del gráfico no es exactamente horizontal, sino que tiene una pendiente Ep pequeña.
Si desea cambiar los valores para el límite elástico y el módulo de elasticidad, active la casilla de verificación "Material definido por el usuario" en la pestaña 'Datos principales'.
Para una definición bilineal , también puede introducir un valor para Ep.
Se pueden definir relaciones más complejas entre la tensión y la deformación por medio del "Diagrama tensión-deformación". Al seleccionar esta opción, se muestra la pestaña 'Diagrama tensión-deformación'.
Defina un punto para la relación tensión-deformación en cada fila de la tabla. La forma en que avanza el diagrama después del último punto de definición se puede seleccionar en la lista 'Fin de diagrama' debajo del diagrama:
En el caso de 'Desgarro', la tensión después del último punto de definición vuelve a cero. 'Fluencia' significa que la tensión permanece constante cuando aumenta la deformación. 'Continuo' significa que la gráfica continúa con la pendiente de la última sección.
Isótropo | Plástico (superficies/sólidos)
Al seleccionar el "Isótropo | Plástico (superficies/sólidos)" en la lista desplegable 'Modelo de material', se habilita la pestaña para introducir parámetros de material no lineal.
Wählen Sie zunächst die 'Spannungsversagenshypothese' aus. Zur Auswahl stehen diese Hipótesis:
Primero, seleccione los 'Criterios de fallo basado en tensiones'. Los siguientes criterios están disponibles para su selección:
- von Mises (criterio de plasticidad de von Mises)
- Tresca (criterio de plasticidad de Tresca)
- Drucker-Prager
- Mohr-Coulomb
Al seleccionar "von Mises", se utiliza la siguiente tensión en el diagrama tensión-deformación:
Superficies:
Sólidos:
Según la hipótesis de "Tresca", se utiliza la siguiente tensión:
Superficies:
Sólidos:
Según la hipótesis de "Drucker-Prager", se utiliza la siguiente tensión para superficies y sólidos:
| σc | Tensión límite para compresión |
| σt | Limitar la tensión por tracción |
Según la hipótesis de "Mohr-Coulomb", se utiliza la siguiente tensión para superficies y sólidos:
Isótropo | Elástico no lineal (barras)
La funcionalidad corresponde en gran medida a la del modelo de material plástico isótropo (barras). La diferencia es que no queda deformación plástica tras la descarga.
Isótropo | Elástico no lineal (superficies/sólidos)
La funcionalidad corresponde en gran medida a la del modelo de material plástico isótropo (superficies/sólidos). La diferencia es que no queda deformación plástica tras la descarga.
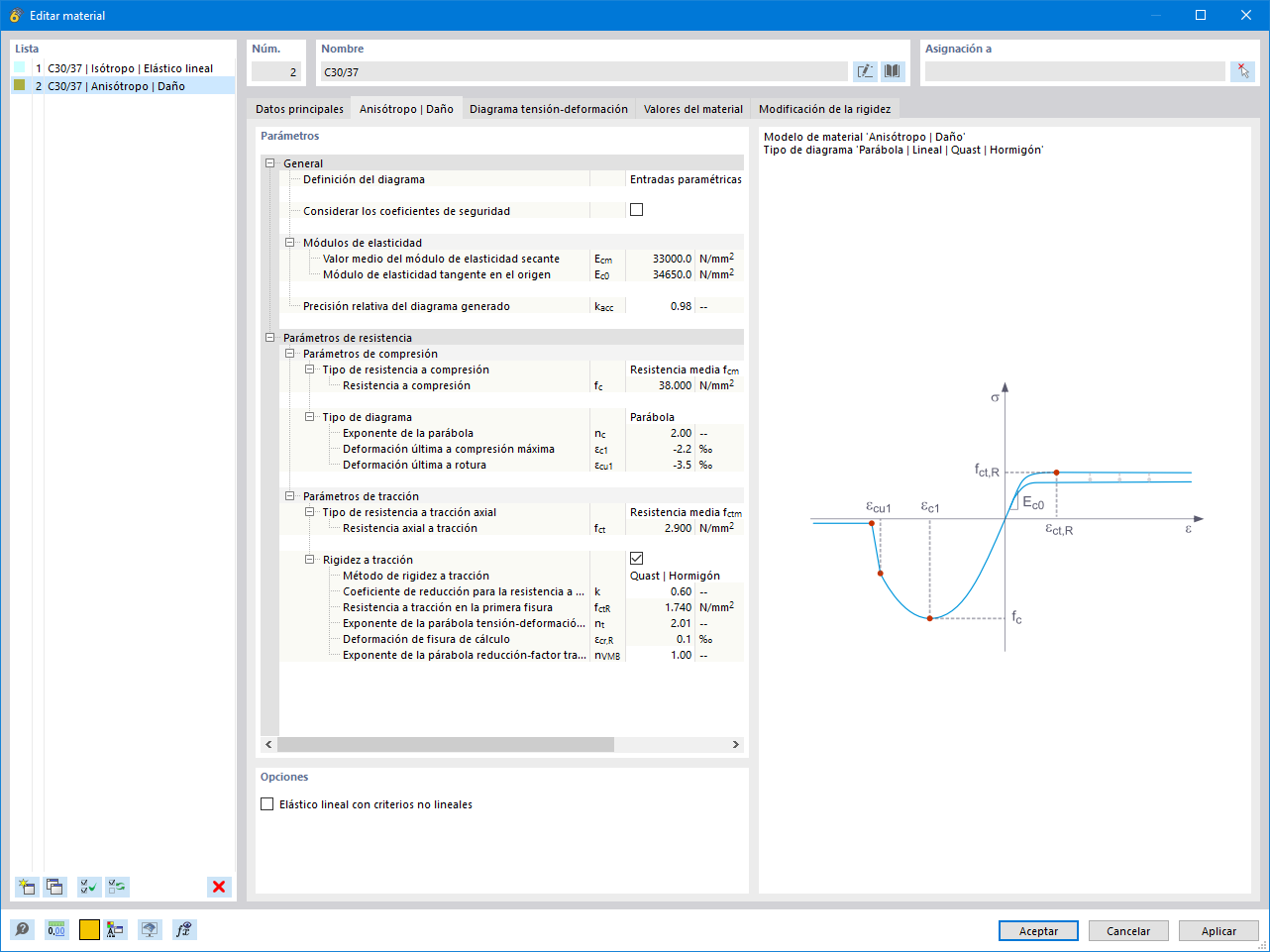
Isótropo | Daño (superficies/sólidos)
A diferencia de otros modelos de material, el diagrama tensión-deformación para este modelo de material no es antimétrico con respecto al origen. Por lo tanto, el comportamiento del hormigón reforzado con fibras de acero se puede mostrar con este modelo de material, por ejemplo. Encuentre información detallada sobre el modelado de hormigón armado con fibras de acero en el artículo técnico sobre Determinación de las propiedades del material de fibras de acero hormigón armado.
En este modelo de material, la rigidez isótropa se reduce con un parámetro de daños escalar. Este parámetro de daños se determina a partir de la curva de tensión definida en el diagrama. No se tiene en cuenta la dirección de las tensiones principales. Más bien, el daño se produce en la dirección de la deformación equivalente, que también cubre la tercera dirección perpendicular al plano. El área de tracción y compresión del tensor de tensiones se trata por separado. En cada caso se aplican diferentes parámetros de daños.
El "Tamaño del elemento de referencia" controla cómo se aplica la escala de la deformación en el área de la fisura respecto a la longitud del elemento. Con el valor predeterminado cero, no se realiza ninguna escala. Por lo tanto, el comportamiento del material de hormigón con fibras de acero se modela de manera realista.
Encuentre más información sobre los antecedentes teóricos del modelo de material 'Daño isótropo' en el artículo técnico que describe el [https://www.dlubal.com/es/soporte-y-formacion/soporte/base-de-datos-de-conocimientos/001461 Daño del modelo de material no lineal.
Ortótropo | Plástico (superficies) / Ortótropo | Plástico (sólidos)
El modelo de material según "Tsai-Wu" unifica el plástico con propiedades ortótropas. De esta manera, es posible modelar específicamente los materiales con propiedades anisótropas, como los plásticos reforzados con fibras o la madera.
Si el material está plastificado, las tensiones permanecen constantes. Se produce una redistribución según las rigideces disponibles en las direcciones individuales.
BILD
BILD
El área elástica corresponde al modelo de material Ortótropo. La siguiente condición de fluencia según Tsai-Wu se aplica a la zona plástica:
Superficies (2D):
FORMEL
Sólidos (3D):
FORMEL
Todas las resistencias se deben definir positivamente.
Puede pensar en el criterio de tensión como una superficie elíptica en un espacio de tensión de seis dimensiones. Si se aplica una de las tres componentes como un valor constante, la superficie se puede proyectar en un espacio de tensiones tridimensional.
Si el valor para fy (σ) según la ecuación de Tsai-Wu, condición de tensión plana, es menor que 1, las tensiones están en la zona elástica. La zona plástica se alcanza tan pronto como fy (σ) = 1. No se admiten valores superiores a 1. El comportamiento del modelo es plástico ideal, lo que significa que no hay rigidez.