Manuels en ligne Connaissances de base de RFEM 6

Retour aux manuels en ligne

159x

004088

28.09.2023

Sélectionner le Manuel

Aperçu

Calcul

Éléments finis

Non-linéarité du matériau

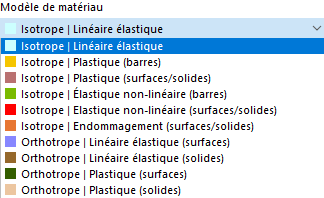
Si le module complémentaire Comportement non linéaire du matériau est activé (licence requise) dans les Données de base du modèle, d'autres options peuvent être sélectionnées dans la liste des modèles de matériau, en plus des modèles de matériau 'Isotrope | Linéaire élastique' et 'Orthotrope | Linéaire élastique ».

Modèle de matériau pour le module d'analyse « Comportement non linéaire du matériau »

Modèles de matériau pour le module d'analyse « Comportement non linéaire du matériau »

Si vous utilisez des modèles de matériaux non linéaires dans RFEM, un calcul itératif est toujours effectué. Selon le modèle de matériau, une relation différente est définie entre les contraintes et les déformations.

La rigidité des éléments finis est ajustée à plusieurs reprises au cours des itérations jusqu'à ce que la relation contrainte-déformation soit satisfaite. L'ajustement est toujours effectué pour l'ensemble d'une surface ou d'un élément de solide. Il est donc recommandé de toujours utiliser le type de lissage Constant sur les éléments de maillage pour l'évaluation des contraintes.

Lissage de résultats

Certains modèles de matériau dans RFEM sont indiqués par « Plastique », d'autres par « Élastique non linéaire ».

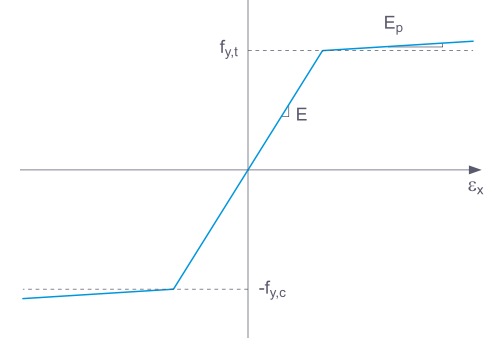
Si un composant structural avec un matériau élastique non linéaire est à nouveau relâché, la déformation reprend la même trajectoire. Lorsqu'il est complètement déchargé, il n'y a plus de déformation.

Diagramme contrainte-déformation, élastique non linéaire

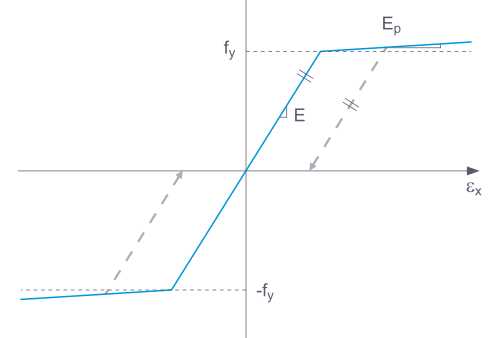
Lors du déchargement d'un composant structural avec un modèle de matériau Plastique, la déformation reste après le déchargement complet.

Diagramme contrainte-déformation plastique

Des informations générales sur les modèles de matériaux non linéaires sont disponibles dans l'article technique décrivant les {%}https://www.dlubal.com/fr/support-et-formation/support/base-de-connaissance/000968 Lois d'élasticité dans les isotropes non linéaires élastiques modèle de matériau.]]

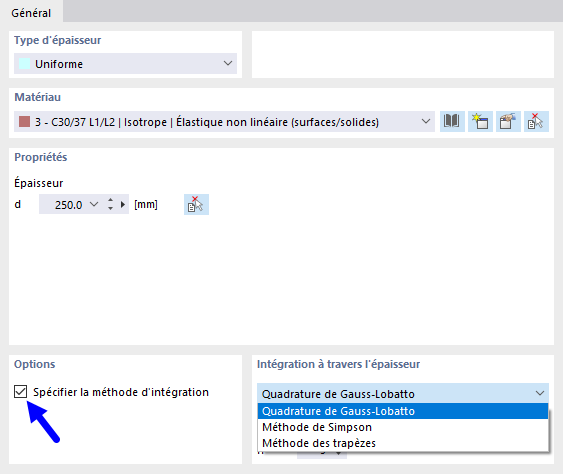
Les efforts internes dans les plaques avec un matériau non linéaire résultent de l’intégration numérique des contraintes sur l’épaisseur de la plaque. Pour définir la méthode d'intégration de l'épaisseur, sélectionnez l'option Spécifier la méthode d'intégration dans la boîte de dialogue {$>Modifier l'épaisseur'. Les méthodes d'intégration suivantes sont donc disponibles :

Quadrature de Gauss-Lobatto
Méthode de Simpson
Méthode des trapèzes

Définir la méthode d'intégration pour l'épaisseur de surface

De plus, vous pouvez préciser le « Nombre de points d'intégration » sur l'épaisseur de la dalle de 3 à 99.

Informations

Une explication théorique des différentes méthodes d'intégration est disponible dans le {%}https://www.dlubal.com/fr/telechargements-et-informations/documents/manuels-en-ligne/rfem-6- manuel en ligne multicouche-surface-laminate-clt/003939 Surfaces multicouches ]].

Plastique isotrope (barres)

Si vous avez sélectionnez Isotrope | Plastique (barres) dans la liste déroulante « Modèle de matériau », l'onglet de saisie des paramètres de matériau non linéaire s'active.

Activer le modèle de matériau non linéaire

Définir les paramètres de matériau non linéaire

Cet onglet permet de définir le diagramme contrainte-déformation. Vous pouvez procéder de plusieurs manières :

Formation sur les fonctions de base
Bilinéaire
Diagramme contrainte-déformation

Si Basique ' est sélectionné, RFEM utilise un modèle de matériau bilinéaire. Les valeurs de la base de données des matériaux sont utilisées pour le module d'élasticité E et la limite d'élasticité f_y Pour des raisons numériques, la branche du graphique n'est pas exactement horizontale, mais a une faible inclinaison E_p.

Si vous souhaitez modifier les valeurs de la limite d'élasticité et du module d'élasticité, cochez la case « Matériau défini par l'utilisateur » dans l'onglet 'Général'.

Activer le matériau défini par l'utilisateur

Pour une définition bilinéaire , vous pouvez également entrer une valeur pour E_p.

Des relations plus complexes entre contrainte et déformation peuvent être définies à l'aide du « diagramme contrainte-déformation ». Lorsque vous sélectionnez cette option, l'onglet « Diagramme contrainte-déformation » s'affiche.

Entrer un diagramme contrainte-déformation défini par l'utilisateur

Définissez un point pour la relation contrainte-déformation dans chaque ligne du tableau. Le cheminement du diagramme après le dernier point de définition peut être sélectionné dans la liste « Fin de diagramme » sous le diagramme :

Distribution après le dernier point de définition

Dans le cas d'une « Rupture », la contrainte après le dernier point de définition revient à zéro. La « Plastification » signifie que la contrainte reste constante lorsque la déformation augmente. « Continu » signifie que le graphique continue avec la pente de la dernière section.

Informations

Dans ce modèle de matériau, le diagramme contrainte-déformation fait référence à la contrainte longitudinale σ_x. Des limites d'élasticité différentes pour la traction et la compression ne peuvent pas être considérées par ce modèle de matériau.

Plastique isotrope (surfaces/solides)

Lors de la sélection du modèle de matériau « Isotrope | Plastique (surfaces/solides) » dans la liste déroulante {$>Modèle de matériau', l'onglet de saisie des paramètres de matériau non linéaire est activé.

Sélectionner le modèle de matériau plastique

Wählen Sie zunächstdie 'SpanungsversagensHypthese' aus. Zur Auswahl stehen diethesen:

Sélectionnez d'abord le « critère de rupture sous contraintes ». Les hypothèses suivantes peuvent être sélectionnées :

von Mises (critère d'élasticité de von Mises)
Tresca (critère d'élasticité de Tresca)
Drucker-Prager
Mohr-Coulomb

Définir le critère de rupture sous contrainte

Lorsque vous sélectionnez « von Mises », la contrainte suivante est utilisée dans le diagramme contrainte-déformation :

Surfaces :

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Contrainte équivalente à partir des contraintes de base selon von Mises

Solides :

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Contrainte équivalente σ_v,Mises à partir des contraintes de base

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Contrainte équivalente σ_{v, Mises} à partir des contraintes principales

Selon l'hypothèse de « Tresca », la contrainte suivante est utilisée :

Surfaces :

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Contraintes équivalentes selon Tresca

Solides :

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Contrainte équivalente σ_v,Tresca

Selon l'hypothèse de « Drucker-Prager », la contrainte suivante est utilisée pour les surfaces et les solides :

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Contrainte limite pour la compression
σ_t	Limiter les contraintes en traction

Critère de rendement selon Drucker-Prager

Selon l'hypothèse de « Mohr-Coulomb », la contrainte suivante est utilisée pour les surfaces et les solides :

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr-Coulomb

Isotrope non linéaire élastique (barres)

Cette fonctionnalité correspond en grande partie à celle du modèle de matériau plastique isotrope (barres). La différence est qu'il n'y a plus de déformation plastique après le déchargement.

Isotrope non linéaire élastique (surfaces/solides)

Cette fonctionnalité correspond en grande partie au modèle de matériau plastique isotrope (surfaces/solides). La différence est qu'il n'y a plus de déformation plastique après le déchargement.

Endommagement isotrope (surfaces/solides)

Contrairement à d'autres modèles de matériau, le diagramme contrainte-déformation de ce modèle de matériau n'est pas antimétrique par rapport à l'origine. Ainsi, le comportement du béton fibré peut être affiché avec ce modèle de matériau, par exemple. Vous trouverez des informations détaillées sur la modélisation du béton fibré dans l'article technique sur Détermination des propriétés de matériau du béton fibré béton armé.

Modèle de matériau « Isotrope | Endommagement »

Dans ce modèle de matériau, la rigidité isotrope est réduite à l'aide d'un paramètre d'endommagement scalaire. Ce paramètre d'endommagement est déterminé à partir de la courbe de contrainte définie dans le diagramme. La direction des contraintes principales n'est pas prise en compte. L'endommagement se produit plutôt dans la direction de la déformation équivalente, qui couvre également la troisième direction perpendiculaire au plan. L'aire de traction et de compression du tenseur des contraintes est traitée séparément. Des paramètres d'endommagement différents s'appliquent dans chaque cas.

La « Taille de l'élément de référence » contrôle la manière dont la déformation dans la zone de la fissure est adaptée à la longueur de l'élément. Avec la valeur par défaut zéro, aucune mise à l'échelle n'est effectuée. Le comportement du béton fibré est ainsi modélisé de manière réaliste.

Vous trouverez plus d'informations sur les principes théoriques du modèle de matériau 'Endommagement isotrope' dans l'article technique [https://www.dlubal.com/fr/support-et-formation/support/base-de-connaissance/| 001461 Modèle de matériau non linéaire Endommagement.

Orthotrope plastique (surfaces) / Orthotrope plastique (solides)

Le modèle de matériau selon « Tsai-Wu » unifie le plastique avec des propriétés orthotropes. Il est ainsi possible de modéliser spécifiquement les matériaux présentant des propriétés anisotropes, tels que les plastiques renforcés de fibres ou le bois.

Lorsque le matériau devient plastique, les contraintes restent constantes. Une redistribution est réalisée selon les rigidités disponibles dans les directions individuelles.

BILD

La zone élastique correspond au type de matériau Orthotrope. La condition d'élasticité suivante selon Tsai-Wu s'applique à la zone plastique :

Surfaces (2D) :

FORMEL

Solides (3D) :

FORMEL

Toutes les résistances doivent être définies comme positives.

Le critère de contrainte peut être imaginé comme une surface en forme d'ellipse dans une zone de contrainte à six dimensions. Si l'une des trois composantes de contrainte est appliquée comme une valeur constante, la surface peut être projetée sur un espace de contraintes tridimensionnel.

Si la valeur de_fy (σ) selon l'équation de Tsai-Wu, condition de contrainte plane est inférieure à 1, les contraintes se trouvent dans la zone élastique. La zone plastique est atteinte dès que_fy (σ) = 1. Les valeurs supérieures à 1 ne sont pas admises. Le modèle se comporte de manière parfaitement plastique, ce qui signifie qu'il ne se raidit pas.

Chapitre parent

Non-linéarité