Con RFEM, tiene la capacidad de analizar varios componentes estructurales, como elementos de barra, placas, muros, láminas y sólidos. Antes de realizar cualquier cálculo, es necesario generar una malla de elementos finitos (EF) que corresponda a los elementos 1D, 2D y 3D deseados.
El análisis por EF implica dividir el sistema estructural en subsistemas más pequeños, cada uno representado por elementos finitos. Se establecen las condiciones de equilibrio para cada uno de estos elementos. Este proceso conduce a la formulación de un sistema lineal de ecuaciones con numerosas variables desconocidas. La precisión de los resultados está directamente influenciada por el nivel de refinamiento en el tamaño de malla de los elementos finitos. Es importante tener en cuenta que una malla más fina mejora la precisión, pero también aumenta significativamente el tiempo de cálculo debido a la mayor cantidad de datos que se procesan. Esto se debe a que se deben resolver ecuaciones adicionales para cada nudo de EF adicional.
Afortunadamente, el software genera automáticamente la malla de EF. No obstante, existen opciones que proporcionan control sobre el proceso de generación de mallas.
Elementos en 1D
Con respecto a los elementos de barra, se asume que la sección mantiene su forma plana durante la deformación. Los elementos de barra 1D se emplean para representar vigas, cerchas, nervios, cables y conexiones rígidas. Cada elemento de barra 1D abarca un total de doce grados de libertad, seis en su punto de inicio y seis en su punto final. Esos grados de libertad se refieren a desplazamientos (ux, uy,uz )y giros (φx,φy,φz ).
En el contexto del análisis estructural lineal, la tracción, compresión y torsión se expresan como funciones lineales a lo largo del eje de la barra (x), independientemente de los efectos de flexión y cortante. Esta representación aproxima estos efectos utilizando un polinomio de tercer orden en x, que también considera la influencia de las tensiones tangenciales resultantes de los esfuerzos cortantes Vy y Vz. La matriz de rigidez KL (12, 12) caracteriza el comportamiento lineal de estos elementos 1D. Además, para escenarios que involucran problemas geométricamente no lineales donde el esfuerzo axil interactúa con la flexión, se emplea la matriz de rigidez KNL (12, 12).
Para cálculos precisos en casos que impliquen deformaciones significativas, se recomienda mejorar la precisión de la malla de elementos finitos (EF) para líneas, como se detalla en el capítulo Refinamientos de malla de líneas de la documentación.
Elementos en 2D
Comúnmente, los elementos cuadriláteros sirven como componentes 2D dentro del análisis estructural. El proceso de generación de mallas introduce elementos triangulares donde se necesitan. Los grados de libertad asociados con los nudos de esquina de los elementos cuadriláteros y triangulares se alinean con los de los elementos 1D, abarcando el desplazamiento (ux, uy,uz )y el giro (φx,φy,φz ). Esta disposición asegura la compatibilidad entre los elementos 1D y 2D en los nudos. Los parámetros se definen inicialmente en el sistema de coordenadas plano local de los elementos y posteriormente se transforman en el sistema de coordenadas global durante la creación de la matriz de rigidez global.
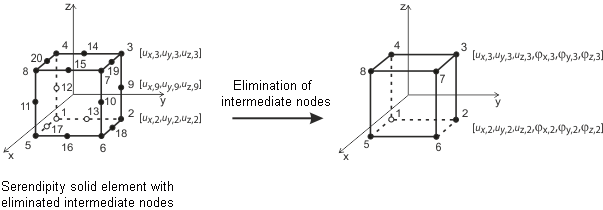
Los elementos planos de láminas están basados en la teoría de Mindlin/Reissner. La representación gráfica en la figura ilustra las aproximaciones de los elementos. Para enlazar directamente con elementos de barra, se adopta un enfoque cuadrado dentro del plano de la lámina (ux,uy ). Esta elección elimina los nudos intermedios, lo que da como resultado un elemento de cuatro nudos con un grado de libertad adicional φx. Esta configuración facilita el acoplamiento directo entre elementos de muro y elementos de viga. Además, se emplean elementos MITC4 ( interpolación mixta de componentes tensoriales) tal como los introdujeron Dvorkin y Bathe [1]. Se basan en una técnica de interpolación mixta que abarca deformaciones transversales, giros de la sección y deformaciones por cortante transversal.
En la actualidad, los elementos de barra se tratan resolviendo la ecuación diferencial del análisis de segundo orden directamente. Sin embargo, cuando se usa la torsión de Saint Venant, no se tienen en cuenta los efectos de alabeo. El análisis de membranas se basa en los principios de Bergan. Por ejemplo, los elementos triangulares se definen al descomponer las funciones fundamentales en tres deformaciones de cuerpo rígido, tres condiciones de deformación constante y tres gradientes lineales específicos de tensión y deformación. Dentro de un elemento, el campo de deformación muestra un comportamiento cuadrático, mientras que el campo de tensiones mantiene la linealidad. La matriz de rigidez del elemento KL se transforma entonces en nueve parámetros combinados de los tiposux, uy, φz. Estos componentes de la matriz se incorporan en la matriz de rigidez general (18, 18), junto con los componentes que contribuyen a los efectos de flexión y cortante, lo que da como resultado el concepto de Lynn/Dhillon.
Posteriormente, el análisis implica la aplicación de placas de Mindlin, donde las placas con distorsiones de cortante distintivas se analizan utilizando los principios de Timoshenko'. Esto permite a RFEM resolver correctamente los problemas relacionados con las placas gruesas y delgadas (placas de Navier). En casos de problemas geométricamente no lineales, la división de las condiciones de tensión-deformación en un estado plano y flexión con interacciones de cortante no es factible. Las interacciones entre estos estados se consideran a través de la matrizKNL. RFEM utiliza una versión simplificada pero eficaz de la matriz KNL, influenciada por los enfoques de Zienkiewicz'. Se emplea la componente cuadrada ε2 del tensor de deformación de Green/Lagrange ε = ε1 + ε2. Se supone una distribución lineal de uz (x, y) bajo la condición de tensión plana y distribuciones lineales de ux (x, y) y uy (x, y) durante la interacción de flexión. Esta suposición es válida debido a que el impacto principal de la interacción depende de la primera derivada de la ecuación diferencial y la rápida reducción en la influencia de los componentes de orden superior con divisiones de elementos más pequeñas. Numerosos análisis numéricos han validado la exactitud de este enfoque.
Cuando se trata de elementos de lámina, es esencial que el espesor de los elementos sea significativamente menor que su extensión. Si no se cumple esta condición, se recomienda modelar los objetos como sólidos. Además, cuando se utilizan elementos de lámina, se debe ejercer una introducción gradual de las tensiones de torsión, ya que el grado de libertad de giro alrededor de la superficie normal es muy sensible.
Elementos en 3D
Los siguientes elementos 3D se implementan en RFEM: tetraedro, pentaedro (prisma, pirámide) y hexaedro. Puede encontrar información detallada sobre los elementos y matrices aplicados en Sevčík Elementos finitos en 3D con grados de libertad rotacional (en checo, disponible a través de Dlubal Software bajo petición).
Generalmente, se deben considerar todos los grados de libertad al giro como críticos para sólidos. Como la deformación del sólido sólo se determina para el desplazamiento de vectores, la rotación de un nodo de malla debida a la singularidad introducida por torsión no afecta a la deformación dentro del sólido, por ejemplo.