Konečné prvky z topologického hlediska

V programu RFEM máte možnost analyzovat různé konstrukční prvky, jako jsou prutové prvky, desky, stěny, skořepiny a tělesa. Před výpočtem je třeba vygenerovat síť konečných prvků (KP), která odpovídá požadovaným 1D, 2D a 3D prvkům.

Při analýze metodou konečných prvků se systém rozděluje na menší podsystémy, z nichž každý je tvořen konečnými prvky. Pro každý z těchto prvků se vytvoří podmínky rovnováhy. Tento proces vede k formulaci lineárního systému rovnic s mnoha neznámými proměnnými. Přesnost výsledků je přímo ovlivněna mírou zahuštění ve velikosti sítě konečných prvků. Je důležité si uvědomit, že jemnější síť zvyšuje přesnost, ale také výrazně prodlužuje dobu výpočtu vzhledem k většímu množství zpracovávaných dat. Pro každý přídavný uzel sítě KP je totiž třeba řešit další rovnice.

Naštěstí program generuje síť konečných prvků automaticky. Nicméně existují možnosti, které umožňují řídit proces generování sítě.

1D prvky

U prutových prvků se předpokládá, že průřez si během deformace zachová svůj rovinný tvar. 1D prutové prvky se používají pro znázornění nosníků, příhradových nosníků, žeber, lan a tuhých spojů. Každý 1D prutový prvek má celkem dvanáct stupňů volnosti - šest v počátečním a šest v koncovém bodě. Tyto stupně volnosti se vztahují k posunům (u_x, u_y, u_z ) a pootočení (φ_x, φ_y, φ_z ).

Pokud je aktivován addon Vázané kroucení, je v každém uzlu k dispozici další stupeň volnosti, který lze použít pro zohlednění deplanace.

V souvislosti s lineární statickou analýzou se tah, tlak a kroucení vyjadřují jako lineární funkce podél osy prutu (x) nezávisle na ohybových a smykových účincích. Toto zobrazení aproximuje tyto účinky pomocí polynomu třetího řádu v_x, který také zohledňuje vliv smykových napětí od posouvajících sil Vy a V_z. Matice tuhosti K_L (12, 12) charakterizuje lineární chování těchto 1D prvků. Kromě toho se pro geometricky nelineární úlohy, kdy normálová síla působí na ohyb, používá matice tuhosti K_NL (12, 12).

Pro přesné výpočty v případech s významnými deformacemi se doporučuje zvýšit přesnost sítě konečných prvků (KP) pro linie, jak je popsáno v kapitole Zahuštění sítě prvků linií.

2D prvky

Čtyřúhelníkové prvky obvykle slouží při statickém výpočtu jako 2D konstrukční prvky. Proces generování sítě prvků zavádí trojúhelníkové prvky tam, kde jsou zapotřebí. Stupně volnosti přiřazené rohovým uzlům čtyřúhelníkových a trojúhelníkových prvků se shodují se stupni volnosti 1D prvků, přičemž zahrnují posun (u_x, u_y, u_z ) a natočení (φ_x, φ_y, φ_z ). Toto uspořádání zajišťuje kompatibilitu mezi 1D a 2D prvky v uzlech. Parametry se nejdříve definují v lokálním rovinném souřadném systému prvků a následně se při vytváření globální matice tuhosti převedou do globálního souřadného systému.

Skořepinové prvky (2D) v programu RFEM

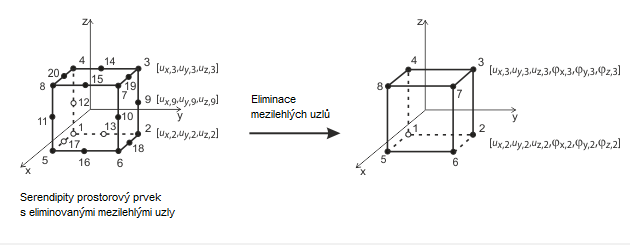
Rovinné skořepinové prvky vycházejí z Mindlinovy/Reissnerovy teorie. Grafické znázornění na obrázku ilustruje přístupy prvků. Pro přímé spojení s prutovými prvky se použije čtvercový přístup v rovině skořepiny (u_x, u_y ). Tato volba odstraní mezilehlé uzly a vytvoří čtyřuzlový prvek s přidaným stupněm volnosti φ_x. Tato konfigurace usnadňuje přímé spojení mezi stěnovými prvky a nosníkovými prvky. Kromě toho se používají prvky MITC4 (smíšená interpolace T ensoriálních komponent) podle Dvorkina a Batha [1]. Spoléhají na smíšenou interpolační techniku, která zahrnuje příčné deformace, natočení průřezu a příčná smyková přetvoření.

V současnosti se prutové prvky řeší přímým řešením diferenciální rovnice druhého řádu. Při použití Saint Venantova kroucení se však deplanační účinky nezohledňují. Analýza membrán je založena na Berganových principech. Například trojúhelníkové prvky jsou definovány rozdělením základních funkcí na tři deformace tuhého tělesa, tři podmínky konstantní deformace a tři specifické lineární gradienty napětí a deformace. Uvnitř prvku vykazuje pole deformace kvadratické chování, zatímco pole napětí si zachovává linearitu. Matice tuhosti prvku K_L se pak převede na devět kombinovaných parametrů typů u_x, u_y, φ_z. Tyto složky matice jsou zahrnuty do celkové matice tuhosti (18, 18) spolu se složkami podílejícími se na ohybových a smykových účincích, což vede k Lynn/Dhillonově koncepci.

Následně se při analýze použijí Mindlinovy desky, kde se podle Timošenko' principů analyzují desky s výraznými smykovými deformacemi. To umožňuje programu RFEM správně řešit problémy týkající se silných i tenkých desek (Navierovy desky). V případě geometricky nelineárních případů není rozdělení napěťových poměrů na rovinný stav a ohyb se smykovými interakcemi proveditelné. Interakce mezi těmito stavy se zohledňují pomocí matice K_NL. RFEM používá zjednodušenou, ale efektivní verzi matice K_NL ovlivněnou Zienkiewiczovými' přístupy. Použije se kvadratická složka ε₂ Greenova/Lagrangeova tenzoru deformace ε = ε₁ + ε₂. Předpokládá se lineární průběh u_z (x, y) při rovinné napjatosti a lineární průběh u_x (x, y) a u_y (x, y) při ohybové interakci. Tento předpoklad je platný vzhledem k tomu, že primární vliv interakce závisí na první derivaci diferenciální rovnice a k rychlému snížení vlivu složek vyššího řádu s menšími dílky prvků. Správnost tohoto přístupu potvrdila řada numerických analýz.

U skořepinových prvků je důležité, aby tloušťka prvků byla výrazně menší než jejich prodloužení. Pokud tato podmínka není splněna, doporučuje se modelovat objekty jako tělesa. Kromě toho by se při použití skořepinových prvků mělo uvažovat postupné zavádění torzních napětí, protože stupeň rotační volnosti okolo normály plochy je velmi citlivý.

3D prvky

V RFEMu se používají následující 3D prvky: čtyřstěn, pětistěn (hranol, jehlan) a šestistěn. Podrobné informace o použitých prvcích a maticích najdete v Sevčíkově 3D konečném prvku se stupni volnosti natočení (na vyžádání u společnosti Dlubal Software).

Těleso (šestistěn)

Obecně platí, že pro tělesa musí být všechny rotační stupně volnosti považovány za kritické. Protože se deformace tělesa stanovuje výlučně z vektorů posunu, potočení uzlu sítě KP např. z důvodu singulárně aplikovaného kroucení nemá vliv na deformaci v tělese.