Com o RFEM, pode analisar vários componentes estruturais, tais como elementos de barra, lajes, paredes, cascas e sólidos. Antes de realizar qualquer cálculo, é necessário gerar uma malha de elementos finitos (EF) que corresponde aos elementos 1D, 2D e 3D desejados.
A análise de EF envolve a divisão do sistema estrutural em subsistemas menores, cada um representado por elementos finitos. As condições de equilíbrio são definidas para cada um destes elementos. Este processo leva à formulaçaõ de um sistema linear de equações com inúmeras variáveis desconhecidas. A precisão dos resultados é diretamente influenciada pelo nível de refinamento no tamanho da malha dos elementos finitos. É importante notar que uma malha mais fina aumenta a precisão, mas também aumenta significativamente o tempo de cálculo devido à maior quantidade de dados a ser processados. Isto deve-se ao facto de ser necessário resolver equações adicionais para cada nó de EF suplementar.
Felizmente, a malha de EF é gerada automaticamente pelo software. No entanto, existem opções que providenciam controlo sobre o processo de geração da malha.
Elementos 1D
No que diz respeito aos elementos de barra, é assumida que a secção mantém a sua forma plana durante a deformação. Os elementos de barra 1D são utilizados para representar vigas, treliças, nervuras, cabos e ligações rígidas. Cada elemento de barra tem um total de doze graus de liberdade – seis no ponto de iniciação e seis no ponto de extremidade. Esses graus de liberdade referem-se aos deslocamentos (ux, uy, uz ) e às rotações (φx, φy, φz ).
Se o módulo Torção com empenamento estiver ativado, existe um grau de liberdade adicional em cada nó que pode ser utilizado para considerar o empenamento.
No contexto da análise estrutural linear, a tracção, compressão e torção são expressas como funções lineares ao longo do eixo da barra (x), independente dos efeitos de flexão e corte. Esta representação aproxima esses efeitos através de uma poligonal de terceira ordem em x, a qual também tem em consideração a influência das tensões de corte resultantes das forças de corte Vy e Vz. A matriz de rigidez KL (12, 12) caracteriza o comportamento linear destes elementos 1D. Além disso, para cenários envolvendo problemas geometricamente não lineares onde a força axial interage com a flexão, é utilizada a matriz de rigidez KNL (12, 12).
Para cálculos precisos em casos que envolveram deformações significativas, é recomendado aumentar a precisão da malha de elementos finitos (EF) para linhas, como detalhado no Capítulo Refinamentos da malha de linhas da documentação.
Elementos 2D
Geralmente, os elementos quadriláteros servem como componentes 2D na análise estrutural. O processo de geração de malha introduz elementos triangulares onde estes são necessários. Os graus de liberdade associados aos nós de canto dos elementos quadriláteros e triangulares alinham-se com os dos elementos 1D, incluindo o deslocamento (ux, uy, uz ) e a rotação (φx, φy, φz ). Esta disposição assegura a compatibilidade entre os elementos 1D e 2D nos nós. Os parâmetros são inicialmente definidos no sistema de coordenadas plano local dos elementos e posteriormente transformados no sistema de coordenadas global durante a criação da matriz de rigidez global.
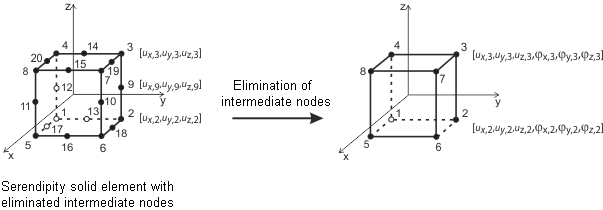
Os elementos de casca planos baseiam-se na teoria Mindlin/Reissner. A representação gráfica na figura ilustra as abordagens dos elementos. Para uma ligação direta com elementos de barra, é adotada uma abordagem quadrática dentro do plano da casca (ux, uy ). Esta escolha elimina os nós intermédios, resultando num elemento de quatro nós com um grau de liberdade adicional φx. Esta configuração facilita o acoplamento direto entre elementos de parede e elementos de barra. Além disso, são utilizados elementos MITC4 ( M ixed I nterpolation of T ensorial C omponents ), introduzidos por Dvorkin e Bathe [1]. Estes baseiam-se numa técnica de interpolação mista que inclui deformações transversais, rotações de secções e extensões de corte transversais.
Atualmente, os elementos de barra são tratados através da resolução direta da equação diferencial da análise de segunda ordem. No entanto, quando é utilizada a torção de Saint Venant, os efeitos de empenamento não são considerados. A análise de membranas é baseada nos princípios de Bergan. Por exemplo, elementos triangulares são definidos dividindo as funções fundamentais em três deformações de corpos rígidos, três condições de deformação constantes e três gradientes lineares específicos de tensões e extensões. Dentro de um elemento, o campo de deformação exibe um comportamento quadrático, enquanto que o campo das tensões mantém uma linearidade. O elemento da matriz rigidez KL é então transformado em nove parâmetros combinados dos tipos ux, uy, φz. Estes componentes da matriz são incorporados na matriz de rigidez global (18, 18), juntamente com os componentes que contribuem para os efeitos de flexão e corte, resultando no conceito Lynn-Dhillon.
Posteriormente, a análise envolve a aplicação das placas de Mindlin, na qual as placas com distorções de corte distintas são analisadas utilizando os princípios de Timoshenko'. Isto permite ao RFEM resolver corretamente problemas relacionados com placas espessas e finas (placas de Navier). Em casos de problemas geometricamente não lineares, a divisão das condições de tensão-deformação para um estado plano e a flexão com interações de corte não são viáveis. As interações entre esses estados são consideradas através da matriz KNL. O RFEM utiliza uma versão simplificada, mas eficaz, da matrizKNL, influenciada pelas abordagens de Zienkiewicz's. O componente quadrático ε2 do tensor de tensões de Green/Lagrange ε = ε1 + ε2 é utilizado. Uma distribuição linear de uz (x, y) sob a condição de tensão plana e as distribuições lineares de ux (x, y) e uy (x, y) durante a interação de flexão são assumidas. Esta suposição é válida devido ao impacto primário da interação depender da primeira derivação da equação diferencial e à rápida redução da influência dos componentes de ordem superior com divisões de elementos menores. Várias análises numéricas confirmaram a exactidão desta abordagem.
Quando se trata de elementos de casca, é essencial que a espessura dos elementos seja significativamente menor do que a sua extensão. Se esta condição não é cumprida, é recomendada a modelação dos objectos como sólidos em vez disso. Além do mais, quando utilizar elementos de casca, deve ser aplicada uma introdução gradual de tensões de torção uma vez que os graus de liberdade de rotação em torno da normal da superfície são altamente sensíveis.
Elementos 3D
Os seguintes elementos 3D são implementados no RFEM tetraedro, pentaedro (prisma, pirâmide) e hexaedro. Informação detalhada sobre elementos e matrizes aplicados pode ser encontrada em Sevčík 3D Finite Elements with Rotational Excellence (em checo, disponível na Dlubal Software).
Geralmente, todos os graus de liberdade de rotação devem ser considerados críticos para sólidos. Como a deformação de um sólido é apenas determinada a partir dos vectores de deslocamento, a rotação de um nó da malha, por exemplo devido à particularidade da rotação introduzida, não afecta a deformação no sólido.